6. 已知 $ \angle AOB = 30^{\circ} $,点 $ P $ 是 $ \angle AOB $ 的平分线 $ OC $ 上的动点,点 $ M $ 在边 $ OA $ 上,且 $ OM = 4 $,则点 $ P $ 到点 $ M $ 与到边 $ OA $ 的距离之和的最小值是多少?
答案:2
解析:
作点$ M $关于$ OC $的对称点$ M' $,过$ M' $作$ M'N \perp OA $于点$ N $,交$ OC $于点$ P $。
因为$ OC $是$ \angle AOB $的平分线,点$ M $与$ M' $关于$ OC $对称,所以$ PM = PM' $,点$ M' $在$ OB $上,且$ OM' = OM = 4 $。
点$ P $到边$ OA $的距离即为$ PN $,所以点$ P $到点$ M $与到边$ OA $的距离之和为$ PM + PN = PM' + PN = M'N $。
在$ Rt\triangle OM'N $中,$ \angle AOB = 30° $,$ OM' = 4 $,所以$ M'N = OM' \cdot \sin 30° = 4 × \frac{1}{2} = 2 $。
故最小值是$ 2 $。
因为$ OC $是$ \angle AOB $的平分线,点$ M $与$ M' $关于$ OC $对称,所以$ PM = PM' $,点$ M' $在$ OB $上,且$ OM' = OM = 4 $。
点$ P $到边$ OA $的距离即为$ PN $,所以点$ P $到点$ M $与到边$ OA $的距离之和为$ PM + PN = PM' + PN = M'N $。
在$ Rt\triangle OM'N $中,$ \angle AOB = 30° $,$ OM' = 4 $,所以$ M'N = OM' \cdot \sin 30° = 4 × \frac{1}{2} = 2 $。
故最小值是$ 2 $。
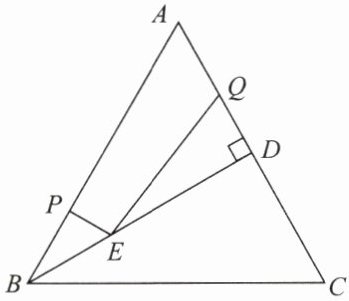
如图,在等边 $ \triangle ABC $ 中,$ BD \perp AC $ 于点 $ D $,点 $ P $,$ Q $ 分别为线段 $ AB $,$ AD $ 上的两个定点,且 $ QD = 15 $,$ BP = AQ = 20 $。
(1)作点 $ Q $ 关于直线 $ BD $ 的对称点 $ Q' $。
(2)在 $ BD $ 上有一动点 $ E $,求 $ PE + QE $ 的最小值。
(1)作点 $ Q $ 关于直线 $ BD $ 的对称点 $ Q' $。
(2)在 $ BD $ 上有一动点 $ E $,求 $ PE + QE $ 的最小值。

答案:
解:
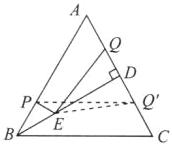
(1)如图所示;
(2)连接PQ',EQ'.
∵△ABC为等边三角形,
∴AC=BA=BC,∠A=60°.
∵BD⊥AC,
∴AD=CD.
∵QD=Q'D,
∴CQ'=AQ=BP=20.
∴AP=AQ'=AQ+2QD=50.
∵∠A=60°,
∴△APQ'为等边三角形,
∴PQ'=AQ'=50.
∵PE+EQ=PE+EQ'≥PQ'=50,
∴当P,E,Q'三点共线时,PE+EQ取最小值50.
解:
(1)如图所示;
(2)连接PQ',EQ'.
∵△ABC为等边三角形,
∴AC=BA=BC,∠A=60°.
∵BD⊥AC,
∴AD=CD.
∵QD=Q'D,
∴CQ'=AQ=BP=20.
∴AP=AQ'=AQ+2QD=50.
∵∠A=60°,
∴△APQ'为等边三角形,
∴PQ'=AQ'=50.
∵PE+EQ=PE+EQ'≥PQ'=50,
∴当P,E,Q'三点共线时,PE+EQ取最小值50.
