1. 下列说法错误的是(
A.关于某条直线对称的两个三角形一定全等
B.轴对称图形至少有一条对称轴
C.全等三角形一定关于某条直线对称
D.角是关于它的平分线所在直线对称的图形
C
)A.关于某条直线对称的两个三角形一定全等
B.轴对称图形至少有一条对称轴
C.全等三角形一定关于某条直线对称
D.角是关于它的平分线所在直线对称的图形
答案:C.
2. 如图,将一块正方形纸片沿对角线折叠一次,然后在得到的三角形的三个角上各挖去一个圆洞,最后将正方形纸片展开,得到的图案是(
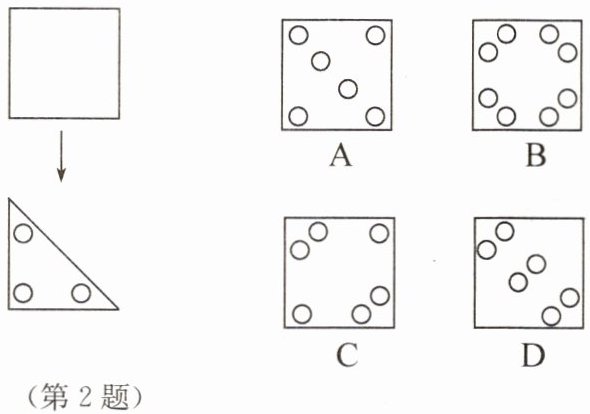
C
)
答案:C.
3. 与点 $ P(-3,2) $ 关于 $ x $ 轴对称的点是(
A.$ (3,2) $
B.$ (-3,2) $
C.$ (3,-2) $
D.$ (-3,-2) $
D
)A.$ (3,2) $
B.$ (-3,2) $
C.$ (3,-2) $
D.$ (-3,-2) $
答案:D.
解析:
关于$x$轴对称的点,横坐标不变,纵坐标互为相反数。点$P(-3,2)$关于$x$轴对称的点,横坐标为$-3$,纵坐标为$-2$,即$(-3,-2)$。
D.
D.
4. 一个等腰三角形的一边长为 $ 7\ cm $,另一边长为 $ 5\ cm $,那么这个等腰三角形的周长为(
A.$ 12\ cm $
B.$ 17\ cm $
C.$ 19\ cm $
D.$ 17\ cm $ 或 $ 19\ cm $
D
)A.$ 12\ cm $
B.$ 17\ cm $
C.$ 19\ cm $
D.$ 17\ cm $ 或 $ 19\ cm $
答案:D.
解析:
情况一:腰长为$7\ cm$,底边长为$5\ cm$。
$7 + 7 + 5 = 19\ cm$,且$7 + 5 > 7$,$7 - 5 < 7$,符合三角形三边关系。
情况二:腰长为$5\ cm$,底边长为$7\ cm$。
$5 + 5 + 7 = 17\ cm$,且$5 + 5 > 7$,$7 - 5 < 5$,符合三角形三边关系。
D.
$7 + 7 + 5 = 19\ cm$,且$7 + 5 > 7$,$7 - 5 < 7$,符合三角形三边关系。
情况二:腰长为$5\ cm$,底边长为$7\ cm$。
$5 + 5 + 7 = 17\ cm$,且$5 + 5 > 7$,$7 - 5 < 5$,符合三角形三边关系。
D.
5. 如图,在 $ \triangle ABC $ 中,$ AB = AD = DC $,$ \angle B = 70^{\circ} $,则 $ \angle C $ 的度数为(
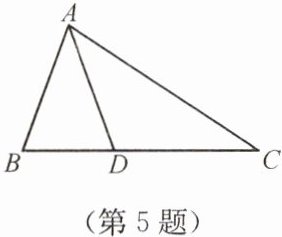
A.$ 35^{\circ} $
B.$ 40^{\circ} $
C.$ 45^{\circ} $
D.$ 50^{\circ} $
A
)
A.$ 35^{\circ} $
B.$ 40^{\circ} $
C.$ 45^{\circ} $
D.$ 50^{\circ} $
答案:A.
解析:
解:在$\triangle ABD$中,$AB=AD$,$\angle B=70^{\circ}$,
$\therefore \angle ADB=\angle B=70^{\circ}$。
$\because \angle ADB+\angle ADC=180^{\circ}$,
$\therefore \angle ADC=180^{\circ}-\angle ADB=110^{\circ}$。
在$\triangle ADC$中,$AD=DC$,
$\therefore \angle C=\angle CAD$。
$\because \angle C+\angle CAD+\angle ADC=180^{\circ}$,
$\therefore 2\angle C+110^{\circ}=180^{\circ}$,
解得$\angle C=35^{\circ}$。
A.
$\therefore \angle ADB=\angle B=70^{\circ}$。
$\because \angle ADB+\angle ADC=180^{\circ}$,
$\therefore \angle ADC=180^{\circ}-\angle ADB=110^{\circ}$。
在$\triangle ADC$中,$AD=DC$,
$\therefore \angle C=\angle CAD$。
$\because \angle C+\angle CAD+\angle ADC=180^{\circ}$,
$\therefore 2\angle C+110^{\circ}=180^{\circ}$,
解得$\angle C=35^{\circ}$。
A.
6. 如图,已知 $ AB = A_1B $,$ A_1B_1 = A_1A_2 $,$ A_2B_2 = A_2A_3 $,$ A_3B_3 = A_3A_4 $,…$ $,若 $ \angle A = 70^{\circ} $,则 $ \angle A_n $ 的度数为(
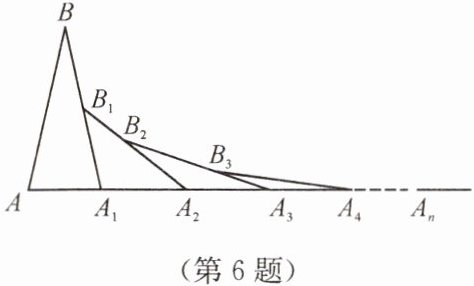
A.$ \dfrac{70^{\circ}}{2^n} $
B.$ \dfrac{70^{\circ}}{2^{n + 1}} $
C.$ \dfrac{70^{\circ}}{2^{n - 1}} $
D.$ \dfrac{70^{\circ}}{2^{n + 2}} $
C
)
A.$ \dfrac{70^{\circ}}{2^n} $
B.$ \dfrac{70^{\circ}}{2^{n + 1}} $
C.$ \dfrac{70^{\circ}}{2^{n - 1}} $
D.$ \dfrac{70^{\circ}}{2^{n + 2}} $
答案:C.
解析:
解:在$\triangle ABA_1$中,$AB = A_1B$,$\angle A = 70°$,
$\angle BA_1A=\angle A=70°$,
$\angle BA_1A$是$\triangle A_1B_1A_2$的外角,$A_1B_1 = A_1A_2$,
$\angle A_2A_1B_1=\angle A_1B_1A_2$,
$\angle BA_1A=\angle A_2A_1B_1+\angle A_1B_1A_2=2\angle A_2A_1B_1$,
$\angle A_2A_1B_1=\frac{70°}{2}$,即$\angle A_2=\frac{70°}{2}$。
同理,$\angle A_3=\frac{\angle A_2}{2}=\frac{70°}{2^2}$,
$\angle A_4=\frac{\angle A_3}{2}=\frac{70°}{2^3}$,
……
依此类推,$\angle A_n=\frac{70°}{2^{n-1}}$。
答案:C
$\angle BA_1A=\angle A=70°$,
$\angle BA_1A$是$\triangle A_1B_1A_2$的外角,$A_1B_1 = A_1A_2$,
$\angle A_2A_1B_1=\angle A_1B_1A_2$,
$\angle BA_1A=\angle A_2A_1B_1+\angle A_1B_1A_2=2\angle A_2A_1B_1$,
$\angle A_2A_1B_1=\frac{70°}{2}$,即$\angle A_2=\frac{70°}{2}$。
同理,$\angle A_3=\frac{\angle A_2}{2}=\frac{70°}{2^2}$,
$\angle A_4=\frac{\angle A_3}{2}=\frac{70°}{2^3}$,
……
依此类推,$\angle A_n=\frac{70°}{2^{n-1}}$。
答案:C
7. 如图,已知正方形 $ ABCD $,且 $ \triangle PAD $ 是等边三角形,则 $ \angle BPC $ 的度数为(
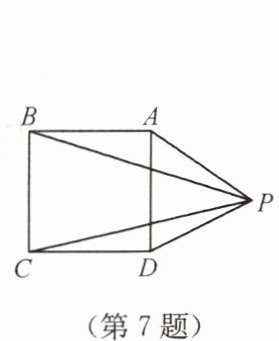
A.$ 30^{\circ} $
B.$ 25^{\circ} $
C.$ 20^{\circ} $
D.$ 15^{\circ} $
A
)
A.$ 30^{\circ} $
B.$ 25^{\circ} $
C.$ 20^{\circ} $
D.$ 15^{\circ} $
答案:A.
解析:
解:设正方形 $ABCD$ 的边长为 $a$。
因为四边形 $ABCD$ 是正方形,所以 $AB=BC=CD=AD=a$,$\angle BAD=\angle ADC=90°$。
因为 $\triangle PAD$ 是等边三角形,所以 $PA=PD=AD=a$,$\angle PAD=\angle PDA=60°$。
所以 $\angle BAP=\angle BAD+\angle PAD=90°+60°=150°$,$\angle CDP=\angle ADC+\angle PDA=90°+60°=150°$。
在 $\triangle ABP$ 中,$AB=PA=a$,$\angle BAP=150°$,所以 $\angle ABP=\angle APB=\frac{180°-150°}{2}=15°$。
同理,在 $\triangle CDP$ 中,$CD=PD=a$,$\angle CDP=150°$,所以 $\angle DCP=\angle DPC=15°$。
在正方形 $ABCD$ 中,$\angle ABC=\angle BCD=90°$,所以 $\angle PBC=\angle ABC-\angle ABP=90°-15°=75°$,$\angle PCB=\angle BCD-\angle DCP=90°-15°=75°$。
在 $\triangle BPC$ 中,$\angle BPC=180°-\angle PBC-\angle PCB=180°-75°-75°=30°$。
答案:A.
因为四边形 $ABCD$ 是正方形,所以 $AB=BC=CD=AD=a$,$\angle BAD=\angle ADC=90°$。
因为 $\triangle PAD$ 是等边三角形,所以 $PA=PD=AD=a$,$\angle PAD=\angle PDA=60°$。
所以 $\angle BAP=\angle BAD+\angle PAD=90°+60°=150°$,$\angle CDP=\angle ADC+\angle PDA=90°+60°=150°$。
在 $\triangle ABP$ 中,$AB=PA=a$,$\angle BAP=150°$,所以 $\angle ABP=\angle APB=\frac{180°-150°}{2}=15°$。
同理,在 $\triangle CDP$ 中,$CD=PD=a$,$\angle CDP=150°$,所以 $\angle DCP=\angle DPC=15°$。
在正方形 $ABCD$ 中,$\angle ABC=\angle BCD=90°$,所以 $\angle PBC=\angle ABC-\angle ABP=90°-15°=75°$,$\angle PCB=\angle BCD-\angle DCP=90°-15°=75°$。
在 $\triangle BPC$ 中,$\angle BPC=180°-\angle PBC-\angle PCB=180°-75°-75°=30°$。
答案:A.
8. 在等边 $ \triangle ABC $ 的内部,按如图所示的方式放置了两个全等的等边 $ \triangle BDE $ 和 $ \triangle FGH $。若求五边形 $ DECHF $ 的周长,则只需知道(
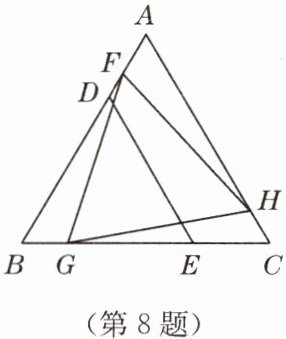
A.$ \triangle ABC $ 的周长
B.$ \triangle AFH $ 的周长
C.四边形 $ FBGH $ 的周长
D.四边形 $ ADEC $ 的周长
A
)
A.$ \triangle ABC $ 的周长
B.$ \triangle AFH $ 的周长
C.四边形 $ FBGH $ 的周长
D.四边形 $ ADEC $ 的周长
答案:A.
解析:
证明:设等边$\triangle ABC$的边长为$a$,等边$\triangle BDE$和$\triangle FGH$的边长均为$b$。
因为$\triangle ABC$是等边三角形,所以$AB=BC=AC=a$,$\angle A=\angle B=\angle C=60°$。
因为$\triangle BDE$是等边三角形,所以$BD=DE=BE=b$,$\angle BDE=\angle BED=60°$。
因为$\triangle FGH$是等边三角形,所以$FG=GH=FH=b$,$\angle FGH=\angle FHG=60°$。
五边形$DECHF$的周长为$DE + EC + CH + HF + FD$。
$DE = b$,$EC = BC - BE = a - b$,$HF = b$。
因为$\triangle FGH$和$\triangle BDE$全等,易证相关线段关系可得$FD + CH = a - b$。
所以五边形$DECHF$的周长为$b + (a - b) + (a - b) + b = 2a$,即只需知道$\triangle ABC$的周长($3a$)即可求出五边形周长。
答案:A
因为$\triangle ABC$是等边三角形,所以$AB=BC=AC=a$,$\angle A=\angle B=\angle C=60°$。
因为$\triangle BDE$是等边三角形,所以$BD=DE=BE=b$,$\angle BDE=\angle BED=60°$。
因为$\triangle FGH$是等边三角形,所以$FG=GH=FH=b$,$\angle FGH=\angle FHG=60°$。
五边形$DECHF$的周长为$DE + EC + CH + HF + FD$。
$DE = b$,$EC = BC - BE = a - b$,$HF = b$。
因为$\triangle FGH$和$\triangle BDE$全等,易证相关线段关系可得$FD + CH = a - b$。
所以五边形$DECHF$的周长为$b + (a - b) + (a - b) + b = 2a$,即只需知道$\triangle ABC$的周长($3a$)即可求出五边形周长。
答案:A