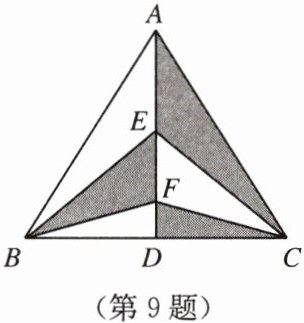
9. 如图,$ \triangle ABD $ 和 $ \triangle ACD $ 关于直线 $ AD $ 对称,若 $ S_{\triangle ABC} = 10 $,则图中阴影部分的面积为
5
。
答案:5.
解析:
因为△ABD和△ACD关于直线AD对称,所以AD是△ABC的对称轴,△ABD≌△ACD,S△ABD=S△ACD=$\frac{1}{2}$S△ABC=5。
设AD与BE交于点E,AD与CF交于点F(假设阴影部分由△AEF、△BEF、△CFD等组成,具体根据对称性质),由于对称性,阴影部分面积等于△ABD或△ACD的面积,即5。
5
设AD与BE交于点E,AD与CF交于点F(假设阴影部分由△AEF、△BEF、△CFD等组成,具体根据对称性质),由于对称性,阴影部分面积等于△ABD或△ACD的面积,即5。
5
10. 在 $ \triangle ABC $ 中,若 $ BC = AC $,$ \angle A = 58^{\circ} $,则 $ \angle C = $
64
$ ^{\circ} $,$ \angle B = $58
$ ^{\circ} $。答案:64;58.
解析:
在$\triangle ABC$中,因为$BC = AC$,所以$\triangle ABC$是等腰三角形,$AB$为底边,$AC$和$BC$为腰。根据等腰三角形两腰所对的角相等,可得$\angle B=\angle A$。已知$\angle A = 58^{\circ}$,所以$\angle B = 58^{\circ}$。
因为三角形内角和为$180^{\circ}$,所以$\angle C=180^{\circ}-\angle A-\angle B=180^{\circ}-58^{\circ}-58^{\circ}=64^{\circ}$。
64;58
因为三角形内角和为$180^{\circ}$,所以$\angle C=180^{\circ}-\angle A-\angle B=180^{\circ}-58^{\circ}-58^{\circ}=64^{\circ}$。
64;58
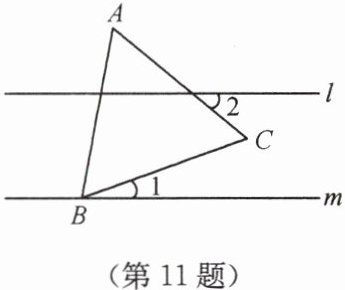
11. 如图,$ l // m $,等边 $ \triangle ABC $ 的顶点 $ B $ 在直线 $ m $ 上,$ \angle 1 = 20^{\circ} $,则 $ \angle 2 = $
40
$ ^{\circ} $。
答案:40.
解析:
解:过点C作CD//m,
∵l//m,
∴CD//l//m,
∴∠BCD=∠1=20°,∠ACD=∠2,
∵△ABC是等边三角形,
∴∠ACB=60°,
∵∠ACB=∠ACD+∠BCD,
∴∠2=∠ACB-∠BCD=60°-20°=40°。
故答案为:40。
∵l//m,
∴CD//l//m,
∴∠BCD=∠1=20°,∠ACD=∠2,
∵△ABC是等边三角形,
∴∠ACB=60°,
∵∠ACB=∠ACD+∠BCD,
∴∠2=∠ACB-∠BCD=60°-20°=40°。
故答案为:40。
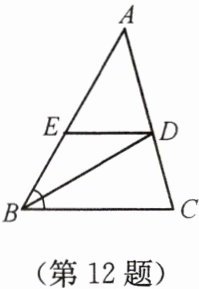
12. 如图,在 $ \triangle ABC $ 中,$ BD $ 平分 $ \angle ABC $,$ ED // BC $,已知 $ AB = 3 $,$ AD = 1 $,则 $ \triangle AED $ 的周长等于
4
。
答案:4.
解析:
证明:
∵ $ ED // BC $,
∴ $ \angle EDB = \angle DBC $。
∵ $ BD $ 平分 $ \angle ABC $,
∴ $ \angle EBD = \angle DBC $,
∴ $ \angle EBD = \angle EDB $,
∴ $ EB = ED $。
∵ $ AB = 3 $,$ AD = 1 $,
∴ $ AE = AB - EB = AB - ED $,$ AC = AD + DC = 1 + DC $。
∵ $ ED // BC $,
∴ $ \triangle AED \sim \triangle ABC $,
∴ $ \frac{AE}{AB} = \frac{AD}{AC} $,即 $ \frac{3 - ED}{3} = \frac{1}{1 + DC} $。
又 $ \frac{ED}{BC} = \frac{AD}{AC} = \frac{1}{1 + DC} $,设 $ ED = x $,则 $ EB = x $,$ AE = 3 - x $,
由 $ \frac{AE}{AB} = \frac{AD}{AC} $ 得 $ \frac{3 - x}{3} = \frac{1}{AC} $,而 $ AC = AB \cdot \frac{AD}{AE} $(相似比),但简化周长计算:
$ \triangle AED $ 周长 $ = AE + ED + AD = (3 - ED) + ED + 1 = 4 $。
答案:4
∵ $ ED // BC $,
∴ $ \angle EDB = \angle DBC $。
∵ $ BD $ 平分 $ \angle ABC $,
∴ $ \angle EBD = \angle DBC $,
∴ $ \angle EBD = \angle EDB $,
∴ $ EB = ED $。
∵ $ AB = 3 $,$ AD = 1 $,
∴ $ AE = AB - EB = AB - ED $,$ AC = AD + DC = 1 + DC $。
∵ $ ED // BC $,
∴ $ \triangle AED \sim \triangle ABC $,
∴ $ \frac{AE}{AB} = \frac{AD}{AC} $,即 $ \frac{3 - ED}{3} = \frac{1}{1 + DC} $。
又 $ \frac{ED}{BC} = \frac{AD}{AC} = \frac{1}{1 + DC} $,设 $ ED = x $,则 $ EB = x $,$ AE = 3 - x $,
由 $ \frac{AE}{AB} = \frac{AD}{AC} $ 得 $ \frac{3 - x}{3} = \frac{1}{AC} $,而 $ AC = AB \cdot \frac{AD}{AE} $(相似比),但简化周长计算:
$ \triangle AED $ 周长 $ = AE + ED + AD = (3 - ED) + ED + 1 = 4 $。
答案:4
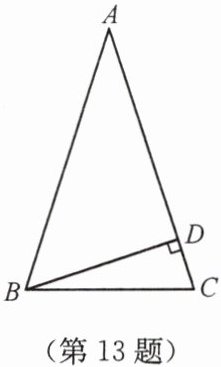
13. 如图,在等腰 $ \triangle ABC $ 中,$ AB = AC $,$ \angle A = 36^{\circ} $,$ BD \perp AC $ 于点 $ D $,则 $ \angle CBD = $
$18°$
。
答案:$18°$.
解析:
解:在等腰$\triangle ABC$中,$AB = AC$,$\angle A = 36^{\circ}$,
$\therefore \angle ABC=\angle C=\frac{180^{\circ}-\angle A}{2}=\frac{180^{\circ}-36^{\circ}}{2}=72^{\circ}$。
$\because BD\perp AC$,
$\therefore \angle BDC = 90^{\circ}$,
$\therefore \angle CBD=90^{\circ}-\angle C=90^{\circ}-72^{\circ}=18^{\circ}$。
故答案为:$18^{\circ}$。
$\therefore \angle ABC=\angle C=\frac{180^{\circ}-\angle A}{2}=\frac{180^{\circ}-36^{\circ}}{2}=72^{\circ}$。
$\because BD\perp AC$,
$\therefore \angle BDC = 90^{\circ}$,
$\therefore \angle CBD=90^{\circ}-\angle C=90^{\circ}-72^{\circ}=18^{\circ}$。
故答案为:$18^{\circ}$。
14. 如图,已知在 $ \triangle ABC $ 中,$ DE $ 是 $ BC $ 的垂直平分线,垂足为 $ E $,交 $ AC $ 于点 $ D $。若 $ AB = 6 $,$ AC = 9 $,则 $ \triangle ABD $ 的周长是______。
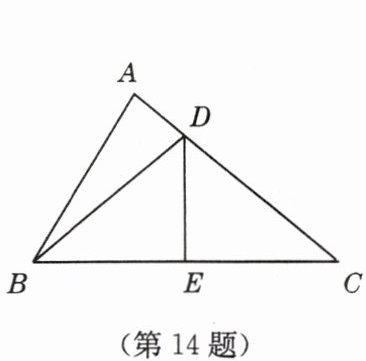

15
答案:15.
解析:
∵DE是BC的垂直平分线,
∴DB=DC。
∵AB=6,AC=9,
∴△ABD的周长=AB+AD+DB=AB+AD+DC=AB+AC=6+9=15。
15
15. 点 $ (-3,1) $ 和 $ (1,1) $ 关于直线
$x=-1$
对称。答案:$x=-1$.
解析:
因为点$(-3,1)$和$(1,1)$的纵坐标相同,所以两点关于过线段中点且垂直于$x$轴的直线对称。线段中点的横坐标为$\frac{-3 + 1}{2}=-1$,故对称直线为$x=-1$。
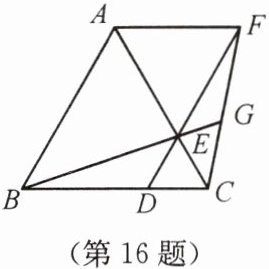
16. 如图,已知 $ \triangle ABC $ 是等边三角形,点 $ D $,$ E $ 分别在边 $ BC $,$ AC $ 上,且 $ CD = CE $,连接 $ DE $ 并延长至点 $ F $,使 $ EF = AE $,连接 $ AF $,$ CF $,连接 $ BE $ 并延长交 $ CF $ 于点 $ G $。下列结论:
(1)$ \triangle ABE \cong \triangle ACF $;
(2)$ BC = DF $;
(3)$ S_{\triangle ABC} = S_{\triangle ACF} + S_{\triangle DCF} $。
其中正确的结论是
(1)$ \triangle ABE \cong \triangle ACF $;
(2)$ BC = DF $;
(3)$ S_{\triangle ABC} = S_{\triangle ACF} + S_{\triangle DCF} $。
其中正确的结论是
(1)(2)(3)
。(填写所有正确结论的序号)
答案:
(1)
(2)
(3).
(1)
(2)
(3).
17. (4 分)如图,已知点 $ P $ 在 $ \angle AOB $ 内,点 $ M $,$ N $ 分别是点 $ P $ 关于 $ OA $,$ OB $ 的对称点,连接 $ M $,$ N $ 分别交 $ OA $,$ OB $ 于 $ E $,$ F $,若 $ \triangle PEF $ 的周长为 15,求 $ MN $ 的长。
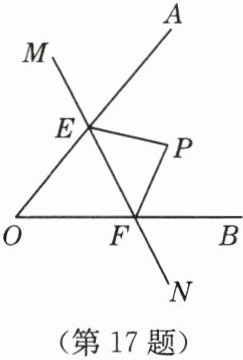

答案:$MN=15$.
解析:
证明:
∵点 $ M $,$ N $ 分别是点 $ P $ 关于 $ OA $,$ OB $ 的对称点,
∴ $ OA $ 垂直平分 $ PM $,$ OB $ 垂直平分 $ PN $,
∴ $ EM = EP $,$ FN = FP $。
∵ $ \triangle PEF $ 的周长为 $ 15 $,
∴ $ EP + EF + FP = 15 $。
∵ $ MN = ME + EF + FN $,
∴ $ MN = EP + EF + FP = 15 $。
$ MN = 15 $
∵点 $ M $,$ N $ 分别是点 $ P $ 关于 $ OA $,$ OB $ 的对称点,
∴ $ OA $ 垂直平分 $ PM $,$ OB $ 垂直平分 $ PN $,
∴ $ EM = EP $,$ FN = FP $。
∵ $ \triangle PEF $ 的周长为 $ 15 $,
∴ $ EP + EF + FP = 15 $。
∵ $ MN = ME + EF + FN $,
∴ $ MN = EP + EF + FP = 15 $。
$ MN = 15 $