18. (5 分)如图,$ A $,$ B $ 是直线 $ MN $ 同侧的两点,在直线 $ MN $ 上求画一点 $ P $,使 $ \angle MPA = \angle NPB $。
答案：画法:
(1)作点 A 关于 MN 的对称点 $A'$;
(2)连接 $A'B$ 交 MN 于点 P,点 P 为所求画的点.
(1)作点 A 关于 MN 的对称点 $A'$;
(2)连接 $A'B$ 交 MN 于点 P,点 P 为所求画的点.
19. (6 分)如图,在 $ \triangle ABC $ 中,$ BD $ 平分 $ \angle ABC $,$ BC $ 的垂直平分线交 $ BC $ 于点 $ E $,交 $ BD $ 于点 $ F $,连接 $ CF $。若 $ \angle A = 60^{\circ} $,$ \angle ABD = 24^{\circ} $,求 $ \angle ACF $ 的度数。
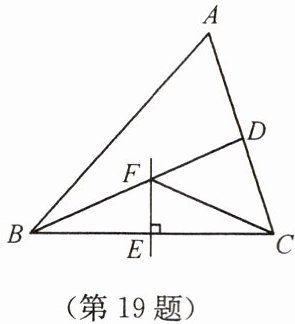
答案：提示:
∵$\angle A=60°$,
∴$\angle ABC+\angle ACB=120°$.证$\angle FCB=\angle DBC$,由$\angle ABD=24°$,得$\angle FCB=\angle DBC=\angle ABD=24°$,
∴$\angle ACF=120° -24° -24° -24° =48°$.
∵$\angle A=60°$,
∴$\angle ABC+\angle ACB=120°$.证$\angle FCB=\angle DBC$,由$\angle ABD=24°$,得$\angle FCB=\angle DBC=\angle ABD=24°$,
∴$\angle ACF=120° -24° -24° -24° =48°$.
20. (6 分)如图,过 $ \angle AOB $ 平分线上一点 $ C $ 作 $ CD // OB $ 交 $ OA $ 于点 $ D $,$ E $ 是线段 $ OC $ 的中点,过点 $ E $ 画直线分别交线段 $ CD $,射线 $ OB $ 于点 $ M $,$ N $,探究线段 $ OD $,$ ON $,$ DM $ 之间的数量关系,并证明你的结论。
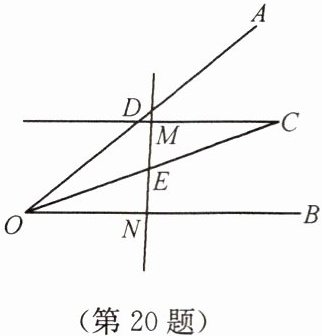
答案：提示:根据 OC 是$\angle AOB$的平分线,$CD// OB$,判断出$\angle DOC=\angle DCO$,所以$OD=CD=DM+CM$;再根据 E 是线段 OC 的中点,$CD// OB$,证明$CM=ON$,即可判断出$OD=DM+ON$.
解析：
证明：
∵OC平分∠AOB，
∴∠DOC=∠BOC．
∵CD//OB，
∴∠DCO=∠BOC，
∴∠DOC=∠DCO，
∴OD=CD．
∵CD=DM+CM，
∴OD=DM+CM．
∵E是OC中点，
∴OE=CE．
∵CD//OB，
∴∠CME=∠ONE．
在△CME和△ONE中，
$\begin{cases} ∠CME=∠ONE \\ ∠CEM=∠OEN \\ CE=OE \end{cases}$，
∴△CME≌△ONE(AAS)，
∴CM=ON．
∴OD=DM+ON．
结论：OD=DM+ON．
∵OC平分∠AOB，
∴∠DOC=∠BOC．
∵CD//OB，
∴∠DCO=∠BOC，
∴∠DOC=∠DCO，
∴OD=CD．
∵CD=DM+CM，
∴OD=DM+CM．
∵E是OC中点，
∴OE=CE．
∵CD//OB，
∴∠CME=∠ONE．
在△CME和△ONE中，
$\begin{cases} ∠CME=∠ONE \\ ∠CEM=∠OEN \\ CE=OE \end{cases}$，
∴△CME≌△ONE(AAS)，
∴CM=ON．
∴OD=DM+ON．
结论：OD=DM+ON．
21. (6 分)如图,已知 $ \triangle ABC $ 为等边三角形,点 $ D $,$ E $ 分别在 $ BC $,$ AC $ 边上,且 $ AE = CD $,$ AD $ 与 $ BE $ 相交于点 $ F $。
(1)求证：$ \triangle ABE \cong \triangle CAD $；
(2)求 $ \angle BFD $ 的度数。
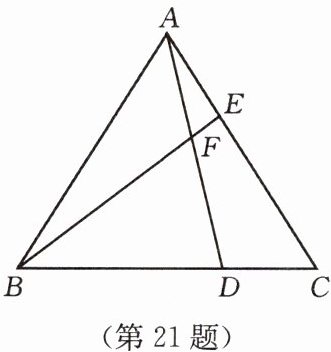
(1)求证：$ \triangle ABE \cong \triangle CAD $；
(2)求 $ \angle BFD $ 的度数。
答案：
(1)证明:
∵$\triangle ABC$是等边三角形,
∴$\angle BAC = \angle C=60°$,$AB=AC$.在$\triangle ABE$和$\triangle CAD$中,$\because AB=AC$,$\angle BAE=\angle C$,$AE=CD$,
∴$\triangle ABE\cong\triangle CAD$(SAS).
(2)$\angle BFD=60°$.
(1)证明:
∵$\triangle ABC$是等边三角形,
∴$\angle BAC = \angle C=60°$,$AB=AC$.在$\triangle ABE$和$\triangle CAD$中,$\because AB=AC$,$\angle BAE=\angle C$,$AE=CD$,
∴$\triangle ABE\cong\triangle CAD$(SAS).
(2)$\angle BFD=60°$.
22. (6 分)如图,已知线段 $ a $,$ h $,求画等腰三角形 $ ABC $,使得底边 $ BC = a $,$ BC $ 边上的高为 $ h $。(保留画图痕迹,不写画法)
答案：
如图,$\triangle ABC$为所求画的图形.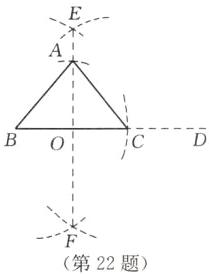
如图,$\triangle ABC$为所求画的图形.