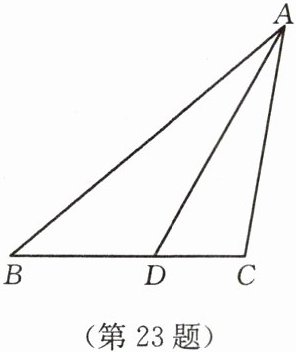
23. (8 分)如图,在 $ \triangle ABC $ 中,$ AC = BC $,$ \angle ACB = 100^{\circ} $,$ AD $ 是角平分线。求证:$ AB = AD + CD $。

答案:证明:在 AB 上截取 $AE = AC$,$AF = AD$,连接 DE,DF.在$\triangle ACD$和$\triangle AED$中,$\left\{\begin{array}{l} AC = AE\\ \angle CAD = \angle EAD\\ AD = AD\end{array}\right.$,
∴$\triangle ACD\cong\triangle AED$.
∴$CD = ED$,$\angle C = \angle AED$.
∵$\angle C = 100°$,
∴$\angle AED = 100°$.
∴$\angle DEF = 80°$.
∵$AC = BC$,
∴$\angle BAC = \angle B = 40°$.
∵AD 是角平分线,
∴$\angle DAE = 20°$.
∵$AD = AF$,
∴$\angle AFD = \angle ADF = 80°$.
∴$\angle DEF = \angle AFD$,$\angle B = \angle FDB = 40°$.
∴$DE = DF$,$DF = BF$.
∴$BF = CD$.
∴$AB = AF + BF = AD + CD$.
∴$\triangle ACD\cong\triangle AED$.
∴$CD = ED$,$\angle C = \angle AED$.
∵$\angle C = 100°$,
∴$\angle AED = 100°$.
∴$\angle DEF = 80°$.
∵$AC = BC$,
∴$\angle BAC = \angle B = 40°$.
∵AD 是角平分线,
∴$\angle DAE = 20°$.
∵$AD = AF$,
∴$\angle AFD = \angle ADF = 80°$.
∴$\angle DEF = \angle AFD$,$\angle B = \angle FDB = 40°$.
∴$DE = DF$,$DF = BF$.
∴$BF = CD$.
∴$AB = AF + BF = AD + CD$.
24. (11 分)
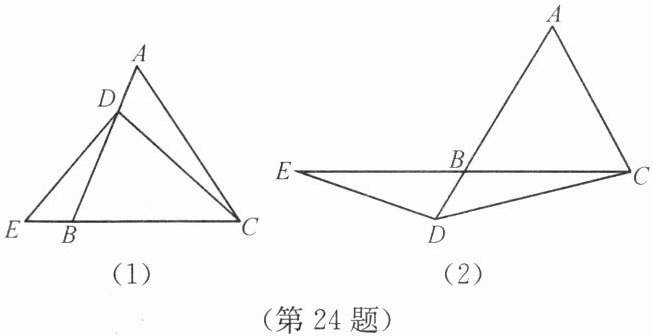
(1)如图(1),$ \triangle ABC $ 是等腰三角形,点 $ D $ 在线段 $ AB $ 上,$ E $ 是直线 $ BC $ 上一点,且 $ \angle DEC = \angle DCE $,若 $ \angle A = 60^{\circ} $。求证:$ EB = AD $。
(2)如图(2),若将(1)中的“点 $ D $ 在线段 $ AB $ 上”改为“点 $ D $ 在线段 $ AB $ 的延长线上”,其他条件不变,(1)中的结论是否成立,并说明理由。
(1)如图(1),$ \triangle ABC $ 是等腰三角形,点 $ D $ 在线段 $ AB $ 上,$ E $ 是直线 $ BC $ 上一点,且 $ \angle DEC = \angle DCE $,若 $ \angle A = 60^{\circ} $。求证:$ EB = AD $。
(2)如图(2),若将(1)中的“点 $ D $ 在线段 $ AB $ 上”改为“点 $ D $ 在线段 $ AB $ 的延长线上”,其他条件不变,(1)中的结论是否成立,并说明理由。

答案:提示:
(1)过点 D 作$DF// BC$交 AC 于点 F,由平行线的性质得出$\angle ADF = \angle ABC$,$\angle AFD = \angle ACB$,$\angle FDC = \angle DCE$,证明$\triangle ABC$是等边三角形,得出$\angle ABC = \angle ACB = 60°$,再证$\triangle ADF$是等边三角形,得$AD = DF$.由已知条件得出$\angle FDC = \angle DEC$,$ED = CD$,根据 AAS 证$\triangle DBE\cong\triangle CFD$,得出$EB = DF = AD$.
(2)成立.过点 D 作$DH// BC$交 AC 的延长线于点 H,同
(1)证出$\triangle DBE\cong\triangle CHD$,得出$EB = DH = AD$.
(1)过点 D 作$DF// BC$交 AC 于点 F,由平行线的性质得出$\angle ADF = \angle ABC$,$\angle AFD = \angle ACB$,$\angle FDC = \angle DCE$,证明$\triangle ABC$是等边三角形,得出$\angle ABC = \angle ACB = 60°$,再证$\triangle ADF$是等边三角形,得$AD = DF$.由已知条件得出$\angle FDC = \angle DEC$,$ED = CD$,根据 AAS 证$\triangle DBE\cong\triangle CFD$,得出$EB = DF = AD$.
(2)成立.过点 D 作$DH// BC$交 AC 的延长线于点 H,同
(1)证出$\triangle DBE\cong\triangle CHD$,得出$EB = DH = AD$.