1. 已知等腰三角形两边的长分别为 $3$ 和 $7$,则此等腰三角形的周长为(
A.$13$
B.$17$
C.$13$ 或 $17$
D.$13$ 或 $10$
B
)A.$13$
B.$17$
C.$13$ 或 $17$
D.$13$ 或 $10$
答案:B
解析:
情况一:腰长为3,底边长为7。
三边长为3,3,7。
因为3+3=6<7,不满足三角形两边之和大于第三边,所以此情况不成立。
情况二:腰长为7,底边长为3。
三边长为7,7,3。
因为7+3=10>7,7+7=14>3,满足三角形两边之和大于第三边,此情况成立。
周长为7+7+3=17。
B
三边长为3,3,7。
因为3+3=6<7,不满足三角形两边之和大于第三边,所以此情况不成立。
情况二:腰长为7,底边长为3。
三边长为7,7,3。
因为7+3=10>7,7+7=14>3,满足三角形两边之和大于第三边,此情况成立。
周长为7+7+3=17。
B
2. 若一个三角形的三个内角度数之比为 $3:2:1$,则与之相邻的三个外角度数之比为(
A.$3:2:1$
B.$1:2:3$
C.$5:4:3$
D.$3:4:5$
D
)A.$3:2:1$
B.$1:2:3$
C.$5:4:3$
D.$3:4:5$
答案:D
解析:
设三角形三个内角分别为$3x$,$2x$,$x$。
由三角形内角和定理得:$3x + 2x + x = 180°$,解得$x = 30°$。
三个内角分别为:$3x = 90°$,$2x = 60°$,$x = 30°$。
相邻外角分别为:$180° - 90° = 90°$,$180° - 60° = 120°$,$180° - 30° = 150°$。
外角之比为$90°:120°:150° = 3:4:5$。
D
由三角形内角和定理得:$3x + 2x + x = 180°$,解得$x = 30°$。
三个内角分别为:$3x = 90°$,$2x = 60°$,$x = 30°$。
相邻外角分别为:$180° - 90° = 90°$,$180° - 60° = 120°$,$180° - 30° = 150°$。
外角之比为$90°:120°:150° = 3:4:5$。
D
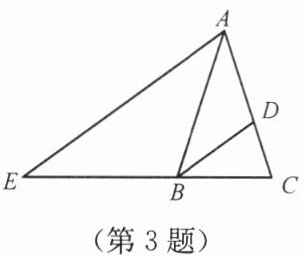
3. 如图,在$\triangle ABC$中,$AB = AC$,$BD平分\angle ABC$交 $AC$ 于点 $D$,$AE// BD$交 $CB$ 的延长线于点 $E$。若$\angle E = 35^{\circ}$,则$\angle BAC$的度数为(
A.$40^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$70^{\circ}$
A
)
A.$40^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$70^{\circ}$
答案:A
解析:
解:
∵AE//BD,∠E=35°,
∴∠DBC=∠E=35°(两直线平行,同位角相等)。
∵BD平分∠ABC,
∴∠ABC=2∠DBC=70°。
∵AB=AC,
∴∠ABC=∠C=70°(等边对等角)。
在△ABC中,∠BAC=180°-∠ABC-∠C=180°-70°-70°=40°。
A
∵AE//BD,∠E=35°,
∴∠DBC=∠E=35°(两直线平行,同位角相等)。
∵BD平分∠ABC,
∴∠ABC=2∠DBC=70°。
∵AB=AC,
∴∠ABC=∠C=70°(等边对等角)。
在△ABC中,∠BAC=180°-∠ABC-∠C=180°-70°-70°=40°。
A
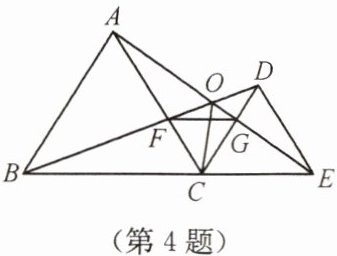
4. 如图,已知$\triangle ABC和\triangle CDE$均是等边三角形,点 $B$,$C$,$E$ 在同一条直线上,$AE$ 与 $BD$ 交于点 $O$,$AE$ 与 $CD$ 交于点 $G$,$BD$ 与 $AC$ 交于点 $F$,连接 $OC$,$FG$,则下列结论:(1)$AE = BD$;(2)$AG = BF$;(3)$\angle BOC = \angle EOC$。其中正确的结论个数是(
A.$0$ 个
B.$1$ 个
C.$2$ 个
D.$3$ 个
D
)
A.$0$ 个
B.$1$ 个
C.$2$ 个
D.$3$ 个
答案:D
解析:
证明:
(1) $\because \triangle ABC$和$\triangle CDE$均是等边三角形,
$\therefore AC=BC$,$CE=CD$,$\angle ACB=\angle DCE=60°$,
$\therefore \angle ACB+\angle ACD=\angle DCE+\angle ACD$,即$\angle ACE=\angle BCD$,
在$\triangle ACE$和$\triangle BCD$中,
$\left\{\begin{array}{l}AC=BC\\ \angle ACE=\angle BCD\\ CE=CD\end{array}\right.$,
$\therefore \triangle ACE≌\triangle BCD(SAS)$,
$\therefore AE=BD$,故
(1)正确;
(2) $\because \triangle ACE≌\triangle BCD$,
$\therefore \angle CAE=\angle CBD$,
$\because \angle ACB=\angle DCE=60°$,点$B$,$C$,$E$在同一条直线上,
$\therefore \angle ACD=60°$,
在$\triangle AGC$和$\triangle BFC$中,
$\left\{\begin{array}{l}\angle CAE=\angle CBD\\ AC=BC\\ \angle ACG=\angle BCF=60°\end{array}\right.$,
$\therefore \triangle AGC≌\triangle BFC(ASA)$,
$\therefore AG=BF$,故
(2)正确;
(3) 过点$C$作$CM\perp AE$于$M$,$CN\perp BD$于$N$,
$\because \triangle ACE≌\triangle BCD$,
$\therefore S_{\triangle ACE}=S_{\triangle BCD}$,
$\because AE=BD$,
$\therefore CM=CN$,
$\because CM\perp AE$,$CN\perp BD$,
$\therefore OC$平分$\angle AOB$,
$\because \angle AOB=120°$,
$\therefore \angle BOC=\angle EOC=60°$,故
(3)正确。
正确的结论个数是$3$个,答案选D。
(1) $\because \triangle ABC$和$\triangle CDE$均是等边三角形,
$\therefore AC=BC$,$CE=CD$,$\angle ACB=\angle DCE=60°$,
$\therefore \angle ACB+\angle ACD=\angle DCE+\angle ACD$,即$\angle ACE=\angle BCD$,
在$\triangle ACE$和$\triangle BCD$中,
$\left\{\begin{array}{l}AC=BC\\ \angle ACE=\angle BCD\\ CE=CD\end{array}\right.$,
$\therefore \triangle ACE≌\triangle BCD(SAS)$,
$\therefore AE=BD$,故
(1)正确;
(2) $\because \triangle ACE≌\triangle BCD$,
$\therefore \angle CAE=\angle CBD$,
$\because \angle ACB=\angle DCE=60°$,点$B$,$C$,$E$在同一条直线上,
$\therefore \angle ACD=60°$,
在$\triangle AGC$和$\triangle BFC$中,
$\left\{\begin{array}{l}\angle CAE=\angle CBD\\ AC=BC\\ \angle ACG=\angle BCF=60°\end{array}\right.$,
$\therefore \triangle AGC≌\triangle BFC(ASA)$,
$\therefore AG=BF$,故
(2)正确;
(3) 过点$C$作$CM\perp AE$于$M$,$CN\perp BD$于$N$,
$\because \triangle ACE≌\triangle BCD$,
$\therefore S_{\triangle ACE}=S_{\triangle BCD}$,
$\because AE=BD$,
$\therefore CM=CN$,
$\because CM\perp AE$,$CN\perp BD$,
$\therefore OC$平分$\angle AOB$,
$\because \angle AOB=120°$,
$\therefore \angle BOC=\angle EOC=60°$,故
(3)正确。
正确的结论个数是$3$个,答案选D。
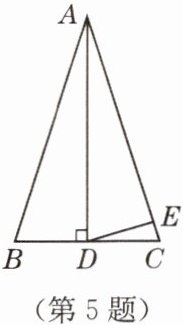
5. 如图,在$\triangle ABC$中,$AD\perp BC$,$AB = AC$,$\angle BAD = 30^{\circ}$,且 $AD = AE$,则$\angle EDC$等于(
A.$10^{\circ}$
B.$12.5^{\circ}$
C.$15^{\circ}$
D.$20^{\circ}$
C
)
A.$10^{\circ}$
B.$12.5^{\circ}$
C.$15^{\circ}$
D.$20^{\circ}$
答案:C
解析:
证明:
∵ $AB = AC$,$AD \perp BC$,
∴ $\angle BAD = \angle CAD = 30°$,$\angle ADC = 90°$,
∴ $\angle BAC = 60°$,$\angle C = \frac{180° - 60°}{2} = 60°$。
∵ $AD = AE$,
∴ $\angle ADE = \angle AED = \frac{180° - 30°}{2} = 75°$。
∵ $\angle ADC = 90°$,
∴ $\angle EDC = \angle ADC - \angle ADE = 90° - 75° = 15°$。
C
∵ $AB = AC$,$AD \perp BC$,
∴ $\angle BAD = \angle CAD = 30°$,$\angle ADC = 90°$,
∴ $\angle BAC = 60°$,$\angle C = \frac{180° - 60°}{2} = 60°$。
∵ $AD = AE$,
∴ $\angle ADE = \angle AED = \frac{180° - 30°}{2} = 75°$。
∵ $\angle ADC = 90°$,
∴ $\angle EDC = \angle ADC - \angle ADE = 90° - 75° = 15°$。
C
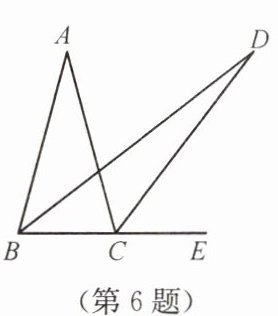
6. 如图,在$\triangle ABC$中,$AB = AC$,$\angle ACB = 75^{\circ}$,$E$ 为 $BC$ 延长线上一点,$\angle ABC$ 与$\angle ACE$ 的平分线相交于点 $D$,则$\angle D$ 的度数为(
A.$15^{\circ}$
B.$17.5^{\circ}$
C.$20^{\circ}$
D.$22.5^{\circ}$
A
)
A.$15^{\circ}$
B.$17.5^{\circ}$
C.$20^{\circ}$
D.$22.5^{\circ}$
答案:A
解析:
解:
∵ $AB = AC$,
∴ $\triangle ABC$ 是等腰三角形,$\angle ABC = \angle ACB = 75°$。
∵ $\angle ACE$ 是 $\triangle ABC$ 的外角,
∴ $\angle ACE = 180° - \angle ACB = 180° - 75° = 105°$。
∵ $BD$ 平分 $\angle ABC$,$CD$ 平分 $\angle ACE$,
∴ $\angle DBC = \frac{1}{2}\angle ABC = \frac{1}{2} × 75° = 37.5°$,
$\angle DCE = \frac{1}{2}\angle ACE = \frac{1}{2} × 105° = 52.5°$。
∵ $\angle DCE$ 是 $\triangle DBC$ 的外角,
∴ $\angle D = \angle DCE - \angle DBC = 52.5° - 37.5° = 15°$。
答案:A
∵ $AB = AC$,
∴ $\triangle ABC$ 是等腰三角形,$\angle ABC = \angle ACB = 75°$。
∵ $\angle ACE$ 是 $\triangle ABC$ 的外角,
∴ $\angle ACE = 180° - \angle ACB = 180° - 75° = 105°$。
∵ $BD$ 平分 $\angle ABC$,$CD$ 平分 $\angle ACE$,
∴ $\angle DBC = \frac{1}{2}\angle ABC = \frac{1}{2} × 75° = 37.5°$,
$\angle DCE = \frac{1}{2}\angle ACE = \frac{1}{2} × 105° = 52.5°$。
∵ $\angle DCE$ 是 $\triangle DBC$ 的外角,
∴ $\angle D = \angle DCE - \angle DBC = 52.5° - 37.5° = 15°$。
答案:A
7. 已知等边三角形的高为$\sqrt{3}$,点 $P$ 为等边三角形内任意一点,则点 $P$ 到三边的距离之和为(
A.$\frac{\sqrt{3}}{2}$
B.$\sqrt{3}$
C.$\frac{3}{2}$
D.不能确定
B
)A.$\frac{\sqrt{3}}{2}$
B.$\sqrt{3}$
C.$\frac{3}{2}$
D.不能确定
答案:B
解析:
设等边三角形的边长为$a$,面积为$S$,点$P$到三边的距离分别为$h_1$、$h_2$、$h_3$。
由等边三角形高为$\sqrt{3}$,根据等边三角形面积公式$S = \frac{1}{2} × a × \sqrt{3}$。
连接$PA$、$PB$、$PC$,将三角形分为三个小三角形,其面积之和为$\frac{1}{2} × a × h_1 + \frac{1}{2} × a × h_2 + \frac{1}{2} × a × h_3$。
因为三个小三角形面积之和等于原三角形面积,所以$\frac{1}{2} × a × \sqrt{3} = \frac{1}{2} × a × (h_1 + h_2 + h_3)$,化简得$h_1 + h_2 + h_3 = \sqrt{3}$。
B
由等边三角形高为$\sqrt{3}$,根据等边三角形面积公式$S = \frac{1}{2} × a × \sqrt{3}$。
连接$PA$、$PB$、$PC$,将三角形分为三个小三角形,其面积之和为$\frac{1}{2} × a × h_1 + \frac{1}{2} × a × h_2 + \frac{1}{2} × a × h_3$。
因为三个小三角形面积之和等于原三角形面积,所以$\frac{1}{2} × a × \sqrt{3} = \frac{1}{2} × a × (h_1 + h_2 + h_3)$,化简得$h_1 + h_2 + h_3 = \sqrt{3}$。
B
8. 平面内点 $A(-1,2)$ 和点 $B(-1,6)$ 的对称轴是(
A.$x$ 轴
B.$y$ 轴
C.直线 $y = 4$
D.直线 $x = -1$
C
)A.$x$ 轴
B.$y$ 轴
C.直线 $y = 4$
D.直线 $x = -1$
答案:C
解析:
点A(-1,2)和点B(-1,6)的横坐标相同,均为-1,说明两点关于平行于y轴的直线对称。两点纵坐标的中点为$\frac{2+6}{2}=4$,所以对称轴是直线$y = 4$。
C
C
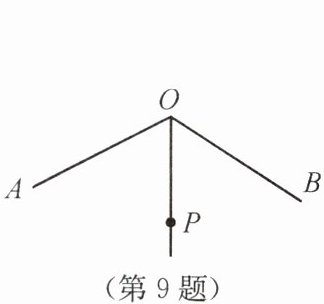
9. 如下图,$\angle AOB = 120^{\circ}$,$OP$ 平分$\angle AOB$,且 $OP = 2$。若点 $M$,$N$ 分别在 $OA$,$OB$ 上,且$\triangle PMN$ 为等边三角形,则满足上述条件的$\triangle PMN$ 有(
A.$1$ 个
B.$2$ 个
C.$3$ 个
D.无数个
D
)
A.$1$ 个
B.$2$ 个
C.$3$ 个
D.无数个
答案:D
解析:
解:
∵OP平分∠AOB,∠AOB=120°,
∴∠AOP=∠BOP=60°。
在OA、OB上分别取点M、N,使∠OPM=∠OPN=60°-θ(θ为任意角),
则∠MPN=60°,且PM=PN,
∴△PMN为等边三角形。
由于θ可任意取值,故满足条件的△PMN有无数个。
D
∵OP平分∠AOB,∠AOB=120°,
∴∠AOP=∠BOP=60°。
在OA、OB上分别取点M、N,使∠OPM=∠OPN=60°-θ(θ为任意角),
则∠MPN=60°,且PM=PN,
∴△PMN为等边三角形。
由于θ可任意取值,故满足条件的△PMN有无数个。
D