27. ($12$ 分)如图,$\triangle ABC$ 是等腰直角三角形,$BC = AC$,直角顶点 $C$ 在 $x$ 轴上,一锐角顶点 $B$ 在 $y$ 轴上。
(1)如图(1),若点 $C$ 的坐标是$(2,0)$,点 $A$ 的坐标是$(-2,-2)$,求点 $B$ 的坐标;
(2)如图(2),若 $y$ 轴恰好平分$\angle ABC$,$AC$ 与 $y$ 轴交于点 $D$,过点 $A$ 作 $AE\perp y$ 轴于点 $E$,求证:$BD = 2AE$。
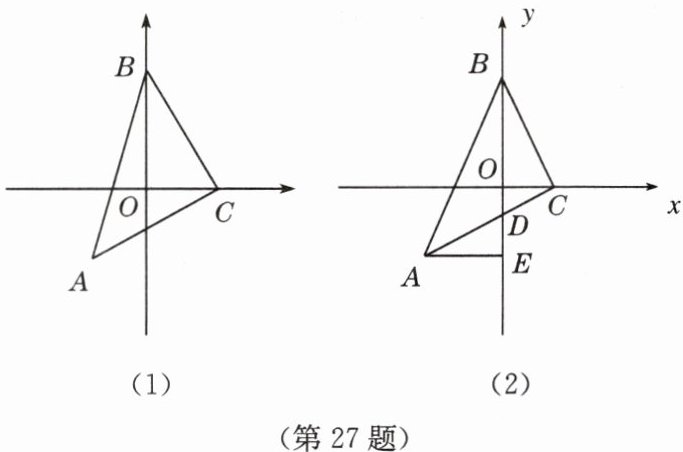
(1)如图(1),若点 $C$ 的坐标是$(2,0)$,点 $A$ 的坐标是$(-2,-2)$,求点 $B$ 的坐标;
(2)如图(2),若 $y$ 轴恰好平分$\angle ABC$,$AC$ 与 $y$ 轴交于点 $D$,过点 $A$ 作 $AE\perp y$ 轴于点 $E$,求证:$BD = 2AE$。

答案:
(1)点B坐标为(0,4).
(2)延长BC,AE交于点F;
∵AC=BC,AC⊥BC,
∴∠BAC=∠ABC=45°.
∵BD平分∠ABC,
∴∠CBD=∠ABD=$\frac{1}{2}$∠ABC=22.5°,∠DAE=90°−∠ABD−∠BAC=22.5°,
∴∠DAE=∠CBD. 在△ACF和△BCD中,$\left\{\begin{array}{l} ∠CAF=∠CBD,\\ AC=BC,\\ ∠ACF=∠BCD=90°, \end{array}\right.$
∴ △ACF≌△BCD(ASA),
∴AF=BD. 在△ABE和△FBE中,$\left\{\begin{array}{l} ∠ABE=∠FBE,\\ BE=BE,\\ ∠AEB=∠FEB=90°, \end{array}\right.$
∴ △ABE≌△FBE(ASA),
∴AE=EF,
∴AF=2AE,
∴BD=2AE.
(1)点B坐标为(0,4).
(2)延长BC,AE交于点F;
∵AC=BC,AC⊥BC,
∴∠BAC=∠ABC=45°.
∵BD平分∠ABC,
∴∠CBD=∠ABD=$\frac{1}{2}$∠ABC=22.5°,∠DAE=90°−∠ABD−∠BAC=22.5°,
∴∠DAE=∠CBD. 在△ACF和△BCD中,$\left\{\begin{array}{l} ∠CAF=∠CBD,\\ AC=BC,\\ ∠ACF=∠BCD=90°, \end{array}\right.$
∴ △ACF≌△BCD(ASA),
∴AF=BD. 在△ABE和△FBE中,$\left\{\begin{array}{l} ∠ABE=∠FBE,\\ BE=BE,\\ ∠AEB=∠FEB=90°, \end{array}\right.$
∴ △ABE≌△FBE(ASA),
∴AE=EF,
∴AF=2AE,
∴BD=2AE.
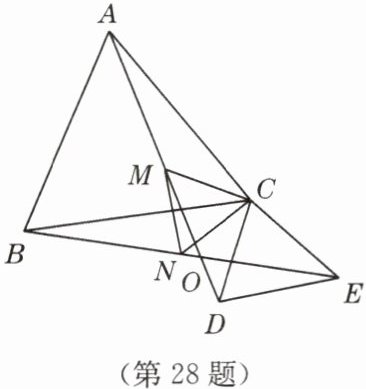
28. ($16$ 分)已知:如图,$\triangle ABC$,$\triangle CDE$ 都是等边三角形,$AD$,$BE$ 相交于点 $O$,点 $M$,$N$ 分别是线段 $AD$,$BE$ 的中点。
(1)求证:$AD = BE$;
(2)求$\angle DOE$ 的度数;
(3)求证:$\triangle MNC$ 是等边三角形。
(1)求证:$AD = BE$;
(2)求$\angle DOE$ 的度数;
(3)求证:$\triangle MNC$ 是等边三角形。

答案:提示:
(1)根据等边三角形性质得出AC=BC,CD=CE,∠ACB=∠DCE=60°,求出∠ACD=∠BCE,证△ACD≌△BCE即可;
(2)由△ACD≌△BCE得∠ADC=∠BEC,∠ADE+∠BED=∠ADC+∠CDE+∠BED=∠BEC+60°+∠BED=∠CED+∠BED+60°=60°+60°=120°,
∴∠DOE=180°−(∠ADE+∠BED)=60°;
(3)证AM=BN,根据SAS证△ACM≌△BCN,推出CM=CN,∠ACM=∠BCN,求出∠NCM=∠BCA=60°即可.
(1)根据等边三角形性质得出AC=BC,CD=CE,∠ACB=∠DCE=60°,求出∠ACD=∠BCE,证△ACD≌△BCE即可;
(2)由△ACD≌△BCE得∠ADC=∠BEC,∠ADE+∠BED=∠ADC+∠CDE+∠BED=∠BEC+60°+∠BED=∠CED+∠BED+60°=60°+60°=120°,
∴∠DOE=180°−(∠ADE+∠BED)=60°;
(3)证AM=BN,根据SAS证△ACM≌△BCN,推出CM=CN,∠ACM=∠BCN,求出∠NCM=∠BCA=60°即可.