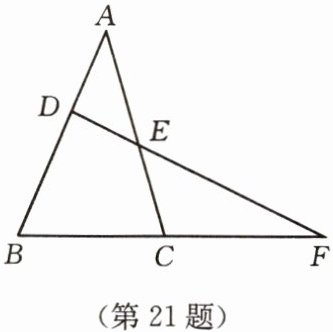
21. ($10$ 分)如图,直线 $DE$ 交$\triangle ABC$ 的边 $AB$,$AC$ 于 $D$,$E$,交 $BC$ 延长线于 $F$,若$\angle B = 67^{\circ}$,$\angle ACB = 74^{\circ}$,$\angle AED = 48^{\circ}$,求$\angle BDF$ 的度数。
答案：87°
解析：
解：在$\triangle ABC$中，$\angle A + \angle B + \angle ACB = 180°$，
$\angle B = 67°$，$\angle ACB = 74°$，
$\angle A = 180° - 67° - 74° = 39°$。
在$\triangle ADE$中，$\angle A + \angle ADE + \angle AED = 180°$，
$\angle AED = 48°$，
$\angle ADE = 180° - \angle A - \angle AED = 180° - 39° - 48° = 93°$。
$\angle BDF + \angle ADE = 180°$（平角定义），
$\angle BDF = 180° - \angle ADE = 180° - 93° = 87°$。
答：$\angle BDF$的度数为$87°$。
$\angle B = 67°$，$\angle ACB = 74°$，
$\angle A = 180° - 67° - 74° = 39°$。
在$\triangle ADE$中，$\angle A + \angle ADE + \angle AED = 180°$，
$\angle AED = 48°$，
$\angle ADE = 180° - \angle A - \angle AED = 180° - 39° - 48° = 93°$。
$\angle BDF + \angle ADE = 180°$（平角定义），
$\angle BDF = 180° - \angle ADE = 180° - 93° = 87°$。
答：$\angle BDF$的度数为$87°$。
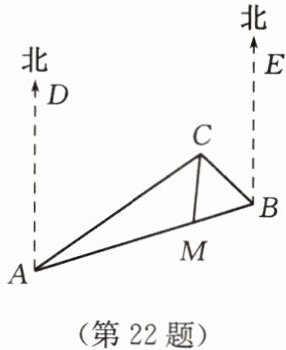
22. ($10$ 分)如图,$C$ 岛在 $A$ 岛的北偏东 $50^{\circ}$方向,$B$ 岛在 $A$ 岛的北偏东 $70^{\circ}$方向,$C$ 岛在 $B$ 岛的北偏西 $40^{\circ}$方向,$\angle ACB$ 的角平分线 $CM$ 与 $AB$ 交于点 $M$,则点 $M$ 在点 $C$ 的什么方向？
答案：点M在点C的南偏西5°方向.
解析：
过点C作CF//AD，过点M作MN//AD。
∵AD//BE，
∴CF//AD//BE，MN//AD//BE。
∵C岛在A岛北偏东50°方向，
∴∠DAC=50°，∠ACF=∠DAC=50°。
∵B岛在A岛北偏东70°方向，
∴∠DAB=70°，∠CAB=∠DAB - ∠DAC=20°。
∵C岛在B岛北偏西40°方向，
∴∠EBC=40°，∠BCF=∠EBC=40°，∠ACB=∠ACF + ∠BCF=90°。
∵CM平分∠ACB，
∴∠ACM=∠BCM=45°，∠MCF=∠ACF - ∠ACM=5°。
∵CF//MN，
∴∠NMC=∠MCF=5°，故点M在点C的南偏西5°方向。
∵AD//BE，
∴CF//AD//BE，MN//AD//BE。
∵C岛在A岛北偏东50°方向，
∴∠DAC=50°，∠ACF=∠DAC=50°。
∵B岛在A岛北偏东70°方向，
∴∠DAB=70°，∠CAB=∠DAB - ∠DAC=20°。
∵C岛在B岛北偏西40°方向，
∴∠EBC=40°，∠BCF=∠EBC=40°，∠ACB=∠ACF + ∠BCF=90°。
∵CM平分∠ACB，
∴∠ACM=∠BCM=45°，∠MCF=∠ACF - ∠ACM=5°。
∵CF//MN，
∴∠NMC=∠MCF=5°，故点M在点C的南偏西5°方向。
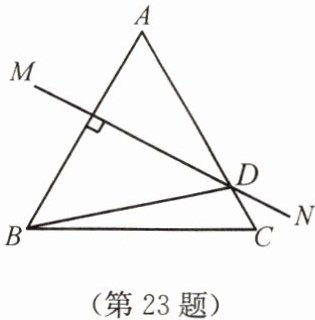
23. ($10$ 分)如图,在等腰$\triangle ABC$中,$AB = AC$,$\angle DBC = 15^{\circ}$,$AB$ 的垂直平分线 $MN$ 交 $AC$ 于点 $D$,求$\angle A$ 的度数。
答案：解：
∵ MN是AB的垂直平分线，
∴ AD=BD.
∴ ∠A=∠ABD.
∵ ∠DBC=15°，
∴ ∠ABC=∠A+15°.
∵ AB=AC，
∴ ∠C=∠ABC=∠A+15°.
∴ ∠A+∠A+15°+∠A+15°=180°，解得∠A=50°.
∵ MN是AB的垂直平分线，
∴ AD=BD.
∴ ∠A=∠ABD.
∵ ∠DBC=15°，
∴ ∠ABC=∠A+15°.
∵ AB=AC，
∴ ∠C=∠ABC=∠A+15°.
∴ ∠A+∠A+15°+∠A+15°=180°，解得∠A=50°.
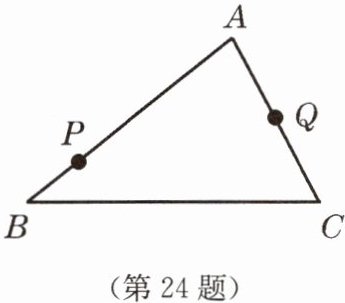
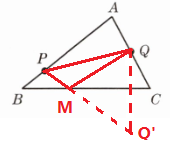
24. ($10$ 分)如图,在$\triangle ABC$中,$P$,$Q$ 分别是边 $AB$,$AC$ 上的定点,在 $BC$ 边上求画一点 $M$,使$\triangle PQM$ 的周长最小。(要求尺规画图,保留清晰画图痕迹,不写画法)
答案：（1）作点P关于BC的对称点P'（尺规作图痕迹：以P为圆心画弧交BC于D、E两点，分别以D、E为圆心，大于1/2DE长为半径画弧，在BC另一侧交于点P'）；
（2）连接P'Q，交BC于点M；
点M即为所求。
（注：图中需保留上述作图痕迹，包括弧线、交点P'、线段P'Q及交点M）
（2）连接P'Q，交BC于点M；
点M即为所求。
（注：图中需保留上述作图痕迹，包括弧线、交点P'、线段P'Q及交点M）
25. ($10$ 分)如图,在$\triangle ABC$中,$\angle B = 55^{\circ}$,$\angle C = 30^{\circ}$,分别以点 $A$ 和点 $C$ 为圆心,大于$\frac{1}{2}AC$ 的长为半径画弧,两弧相交于点 $M$,$N$,作直线 $MN$,交 $BC$ 于点 $D$,连接 $AD$,求$\angle BAD$ 的度数。
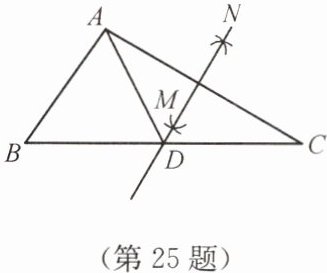
答案：提示：由线段垂直平分线的性质得AD=DC，可得∠DAC=∠C=30°，通过三角形内角和得到∠BAC=95°，求出∠BAD=∠BAC - ∠CAD=65°.
解析：
解：在$\triangle ABC$中，
$\angle BAC=180^{\circ}-\angle B-\angle C=180^{\circ}-55^{\circ}-30^{\circ}=95^{\circ}$，
由作图可知，$MN$是线段$AC$的垂直平分线，
$\therefore AD=DC$，
$\therefore \angle DAC=\angle C=30^{\circ}$，
$\therefore \angle BAD=\angle BAC-\angle DAC=95^{\circ}-30^{\circ}=65^{\circ}$。
答：$\angle BAD$的度数为$65^{\circ}$。
$\angle BAC=180^{\circ}-\angle B-\angle C=180^{\circ}-55^{\circ}-30^{\circ}=95^{\circ}$，
由作图可知，$MN$是线段$AC$的垂直平分线，
$\therefore AD=DC$，
$\therefore \angle DAC=\angle C=30^{\circ}$，
$\therefore \angle BAD=\angle BAC-\angle DAC=95^{\circ}-30^{\circ}=65^{\circ}$。
答：$\angle BAD$的度数为$65^{\circ}$。
26. ($12$ 分)如图,点 $D$ 在$\triangle ABC$ 的边 $BC$ 上,$\angle ADB = \angle ADE$,$\angle BAD = \angle CDE = \angle EAC$。求证：$\triangle ABC\cong\triangle ADE$。
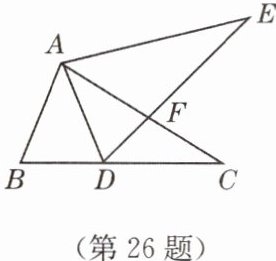
答案：提示：由∠ADC=∠B+∠BAD，∠BAD=∠CDE，得∠B=∠ADE=∠ADB，从而有AB=AD，再利用ASA证得.
解析：
证明：
∵∠ADC是△ABD的外角，
∴∠ADC=∠B+∠BAD。
又
∵∠ADC=∠ADB+∠CDE，且∠BAD=∠CDE，
∴∠B=∠ADB。
∵∠ADB=∠ADE，
∴∠B=∠ADE。
∵∠BAD=∠EAC，
∴∠BAD+∠DAC=∠EAC+∠DAC，即∠BAC=∠DAE。
在△ABC和△ADE中，
$\left\{\begin{array}{l}∠BAC=∠DAE,\\AB=AD,\\∠B=∠ADE,\end{array}\right.$
∴△ABC≌△ADE（ASA）。
∵∠ADC是△ABD的外角，
∴∠ADC=∠B+∠BAD。
又
∵∠ADC=∠ADB+∠CDE，且∠BAD=∠CDE，
∴∠B=∠ADB。
∵∠ADB=∠ADE，
∴∠B=∠ADE。
∵∠BAD=∠EAC，
∴∠BAD+∠DAC=∠EAC+∠DAC，即∠BAC=∠DAE。
在△ABC和△ADE中，
$\left\{\begin{array}{l}∠BAC=∠DAE,\\AB=AD,\\∠B=∠ADE,\end{array}\right.$
∴△ABC≌△ADE（ASA）。