3. 运用乘法公式计算$(x + 3)^{2}$的结果是(
A.$x^{2}+9$
B.$x^{2}-6x + 9$
C.$x^{2}+6x + 9$
D.$x^{2}+3x + 9$
C
)A.$x^{2}+9$
B.$x^{2}-6x + 9$
C.$x^{2}+6x + 9$
D.$x^{2}+3x + 9$
答案:C.
解析:
$(x + 3)^{2}=x^{2}+2× x×3+3^{2}=x^{2}+6x + 9$
C.
C.
问题 运用完全平方公式计算:
(1) $(-3x + 2y)^{2}$;
(2) $(3m - n)(-3m + n)$。
名师指导
(1) $(-3x + 2y)^{2}= (2y - 3x)^{2}或(-3x + 2y)^{2}= (3x - 2y)^{2}$,可以使用差的完全平方公式;
(2) 式子可转化为$(3m - n)(-3m + n)= (3m - n)[-(3m - n)]= -(3m - n)^{2}$,这是一个常用技巧。
解题示范(学生在教师指导下,独立完成)
解:
(1) $(-3x + 2y)^{2}$;
(2) $(3m - n)(-3m + n)$。
名师指导
(1) $(-3x + 2y)^{2}= (2y - 3x)^{2}或(-3x + 2y)^{2}= (3x - 2y)^{2}$,可以使用差的完全平方公式;
(2) 式子可转化为$(3m - n)(-3m + n)= (3m - n)[-(3m - n)]= -(3m - n)^{2}$,这是一个常用技巧。
解题示范(学生在教师指导下,独立完成)
解:
答案:(1)
$\begin{aligned}(-3x + 2y)^{2} &= (2y - 3x)^{2}\\&= (2y)^{2} - 2× 2y× 3x + (3x)^{2}\\&= 4y^{2} - 12xy + 9x^{2}\end{aligned}$
(2)
$\begin{aligned} (3m - n)(-3m + n) &= (3m - n)[-(3m - n)]\\&= -(3m - n)^{2}\\&= -(9m^{2} - 6mn + n^{2})\\&= -9m^{2} + 6mn - n^{2}\end{aligned}$
$\begin{aligned}(-3x + 2y)^{2} &= (2y - 3x)^{2}\\&= (2y)^{2} - 2× 2y× 3x + (3x)^{2}\\&= 4y^{2} - 12xy + 9x^{2}\end{aligned}$
(2)
$\begin{aligned} (3m - n)(-3m + n) &= (3m - n)[-(3m - n)]\\&= -(3m - n)^{2}\\&= -(9m^{2} - 6mn + n^{2})\\&= -9m^{2} + 6mn - n^{2}\end{aligned}$
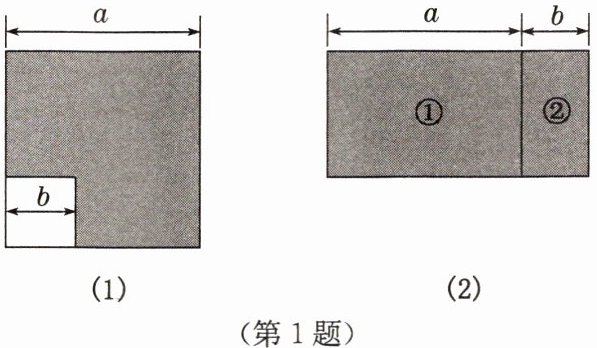
1. 如图(1),在边长为$a的大正方形中剪去一个边长为b$的小正方形,再将图中的阴影部分剪拼成一个长方形。如图(2),这个拼成的长方形的长为$30$,宽为$20$,则图(2)中②部分的面积是(
A.$60$
B.$100$
C.$125$
D.$150$
]
B
)
A.$60$
B.$100$
C.$125$
D.$150$
]
答案:B.
解析:
由图
(1)阴影部分面积为$a^2 - b^2$,图
(2)长方形面积为$(a + b)(a - b)$,两者相等。
已知长方形长$a + b = 30$,宽$a - b = 20$。
联立方程:
$\begin{cases}a + b = 30 \\a - b = 20\end{cases}$
解得$a = 25$,$b = 5$。
图
(2)中②部分为长方形,长为$b$,宽为$a - b$,面积为$b(a - b) = 5×20 = 100$。
B.
(1)阴影部分面积为$a^2 - b^2$,图
(2)长方形面积为$(a + b)(a - b)$,两者相等。
已知长方形长$a + b = 30$,宽$a - b = 20$。
联立方程:
$\begin{cases}a + b = 30 \\a - b = 20\end{cases}$
解得$a = 25$,$b = 5$。
图
(2)中②部分为长方形,长为$b$,宽为$a - b$,面积为$b(a - b) = 5×20 = 100$。
B.
2. 下列各式是完全平方展开式的有(
(1) $x^{2}-2x + 4$;(2) $2m^{2}-2m + 1$;(3) $x^{6}-4x^{3}+4$;(4) $y^{4}+2y + 1$。
A. $1$个
B. $2$个
C. $3$个
D. $4$个
A
)(1) $x^{2}-2x + 4$;(2) $2m^{2}-2m + 1$;(3) $x^{6}-4x^{3}+4$;(4) $y^{4}+2y + 1$。
A. $1$个
B. $2$个
C. $3$个
D. $4$个
答案:A.
解析:
(1) $x^2 - 2x + 4$,中间项应为$\pm 4x$,不是完全平方展开式;
(2) $2m^2 - 2m + 1$,首项系数不是平方数,不是完全平方展开式;
(3) $x^6 - 4x^3 + 4 = (x^3 - 2)^2$,是完全平方展开式;
(4) $y^4 + 2y + 1$,中间项应为$\pm 2y^2$,不是完全平方展开式。
是完全平方展开式的有1个。
A
3. 下列计算正确的是(
A.$(b - 4c)^{2}= b^{2}-16c^{2}$
B.$(a - 2b)^{2}= a^{2}+4ab + 4b^{2}$
C.$(x + y)^{2}= x^{2}+xy + y^{2}$
D.$(4m - n)^{2}= 16m^{2}-8mn + n^{2}$
D
)A.$(b - 4c)^{2}= b^{2}-16c^{2}$
B.$(a - 2b)^{2}= a^{2}+4ab + 4b^{2}$
C.$(x + y)^{2}= x^{2}+xy + y^{2}$
D.$(4m - n)^{2}= 16m^{2}-8mn + n^{2}$
答案:D.
解析:
A.$(b - 4c)^{2}=b^{2}-8bc + 16c^{2}$,故A错误;
B.$(a - 2b)^{2}=a^{2}-4ab + 4b^{2}$,故B错误;
C.$(x + y)^{2}=x^{2}+2xy + y^{2}$,故C错误;
D.$(4m - n)^{2}=16m^{2}-8mn + n^{2}$,故D正确。
D
B.$(a - 2b)^{2}=a^{2}-4ab + 4b^{2}$,故B错误;
C.$(x + y)^{2}=x^{2}+2xy + y^{2}$,故C错误;
D.$(4m - n)^{2}=16m^{2}-8mn + n^{2}$,故D正确。
D