22. (7 分)先化简,再求值:$[(x + y)\cdot(x - y)-(x - y)^{2}+(2x - y)(x - 2y)]÷2x$,其中 $x = -1$,$y = -\frac{2}{3}$。
答案:原式=$(x^{2}-y^{2}-x^{2}+2xy-y^{2}+2x^{2}-5xy+2y^{2})÷(2x)=(2x^{2}-3xy)÷(2x)=x-\frac {3}{2}y$,将$x=-1,y=-\frac {2}{3}$代入得原式$=(-1)-\frac {3}{2}×(-\frac {2}{3})=(-1)-(-1)=0.$
解析:
解:原式$=[(x^{2}-y^{2})-(x^{2}-2xy+y^{2})+(2x^{2}-5xy+2y^{2})]÷2x$
$=(x^{2}-y^{2}-x^{2}+2xy-y^{2}+2x^{2}-5xy+2y^{2})÷2x$
$=(2x^{2}-3xy)÷2x$
$=x-\frac{3}{2}y$
当$x=-1$,$y=-\frac{2}{3}$时,
原式$=-1-\frac{3}{2}×(-\frac{2}{3})$
$=-1+1$
$=0$
$=(x^{2}-y^{2}-x^{2}+2xy-y^{2}+2x^{2}-5xy+2y^{2})÷2x$
$=(2x^{2}-3xy)÷2x$
$=x-\frac{3}{2}y$
当$x=-1$,$y=-\frac{2}{3}$时,
原式$=-1-\frac{3}{2}×(-\frac{2}{3})$
$=-1+1$
$=0$
23. (7 分)大正方形的周长比小正方形的周长长 96 cm,它们的面积相差$ 960 cm^2,$求这两个正方形的边长。
答案:32 cm,8 cm.
解析:
设大正方形的边长为$a\ cm$,小正方形的边长为$b\ cm$。
由题意得:
$\begin{cases}4a - 4b = 96 \\a^2 - b^2 = 960\end{cases}$
化简第一个方程:$a - b = 24$。
第二个方程因式分解:$(a - b)(a + b) = 960$。
将$a - b = 24$代入得:$24(a + b) = 960$,解得$a + b = 40$。
联立$\begin{cases}a - b = 24 \\ a + b = 40\end{cases}$,解得$\begin{cases}a = 32 \\ b = 8\end{cases}$。
大正方形边长为$32\ cm$,小正方形边长为$8\ cm$。
由题意得:
$\begin{cases}4a - 4b = 96 \\a^2 - b^2 = 960\end{cases}$
化简第一个方程:$a - b = 24$。
第二个方程因式分解:$(a - b)(a + b) = 960$。
将$a - b = 24$代入得:$24(a + b) = 960$,解得$a + b = 40$。
联立$\begin{cases}a - b = 24 \\ a + b = 40\end{cases}$,解得$\begin{cases}a = 32 \\ b = 8\end{cases}$。
大正方形边长为$32\ cm$,小正方形边长为$8\ cm$。
24. (11 分)(1)通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式。
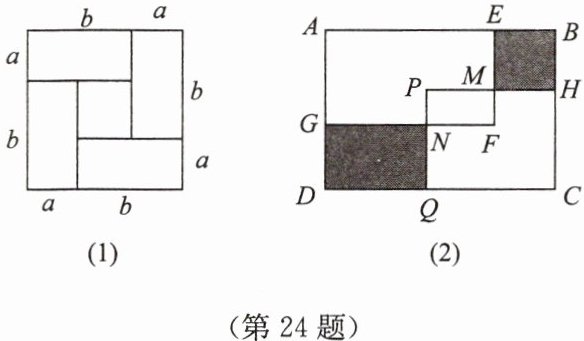
如图(1),有四张长为 $b$、宽为 $a$ 的长方形纸片按如图所示方式拼成了一个正方形,请你通过拼图写出 $(b + a)^{2}$,$ab$,$(b - a)^{2}$ 之间的等量关系是
(2)若 $2a - b = 5$,$ab = 2$,求 $(2a + b)^{2}$ 的值。
(3)如图(2),为创办文明校园,某校计划在面积为 $165$ m^2 的长方形空地 $ABCD(AB>AD)$ 中划出长方形 $AEFG$ 和长方形 $PQCH$,两个长方形重合部分刚好建一个长为 3 m,宽为 2 m 的喷泉水池 $PMFN$。现将图中阴影部分区域作为花圃,且花圃总周长为 42 m,则 $AB - AD$ 的长度为多少米?
如图(1),有四张长为 $b$、宽为 $a$ 的长方形纸片按如图所示方式拼成了一个正方形,请你通过拼图写出 $(b + a)^{2}$,$ab$,$(b - a)^{2}$ 之间的等量关系是
$(b+a)^{2}-(b-a)^{2}=4ab$
。(2)若 $2a - b = 5$,$ab = 2$,求 $(2a + b)^{2}$ 的值。
(3)如图(2),为创办文明校园,某校计划在面积为 $165$ m^2 的长方形空地 $ABCD(AB>AD)$ 中划出长方形 $AEFG$ 和长方形 $PQCH$,两个长方形重合部分刚好建一个长为 3 m,宽为 2 m 的喷泉水池 $PMFN$。现将图中阴影部分区域作为花圃,且花圃总周长为 42 m,则 $AB - AD$ 的长度为多少米?

答案:解:(1)$(b+a)^{2}-(b-a)^{2}=4ab$. (2)
∵$2a-b=5,ab=2$,由(1)可得,$(2a+b)^{2}-(2a-b)^{2}=8ab$,
∴$(2a+b)^{2}-5^{2}=8×2$,解得$(2a+b)^{2}=41$. (3)设$AB=a,AD=b$,根据题意得,$ab=165,PN=MF=2,PM=NF=3$,
∴$GD+QN+ME+BH=2(b-2)=2b-4,BE+MH+GN+DQ=2(a-3)=2a-6$.
∵ 花圃总周长为42 m,
∴$2b-4+2a-6=42$,
∴$a+b=26$. 由(1)可得,$(a+b)^{2}-(a-b)^{2}=4ab$,
∴$26^{2}-(a-b)^{2}=4×165$,
∴$(a-b)^{2}=16$,解得$a-b=4$或$a-b=-4$,
∵$AB>AD$,
∴$a-b=4$,即$AB-AD=4.$
∵$2a-b=5,ab=2$,由(1)可得,$(2a+b)^{2}-(2a-b)^{2}=8ab$,
∴$(2a+b)^{2}-5^{2}=8×2$,解得$(2a+b)^{2}=41$. (3)设$AB=a,AD=b$,根据题意得,$ab=165,PN=MF=2,PM=NF=3$,
∴$GD+QN+ME+BH=2(b-2)=2b-4,BE+MH+GN+DQ=2(a-3)=2a-6$.
∵ 花圃总周长为42 m,
∴$2b-4+2a-6=42$,
∴$a+b=26$. 由(1)可得,$(a+b)^{2}-(a-b)^{2}=4ab$,
∴$26^{2}-(a-b)^{2}=4×165$,
∴$(a-b)^{2}=16$,解得$a-b=4$或$a-b=-4$,
∵$AB>AD$,
∴$a-b=4$,即$AB-AD=4.$