10. (18分)如图是一个“函数求值机”的示意图,其中$y是x$的函数.通过该“函数求值机”得到的几组$x与y$的对应值如下表所示.
根据以上信息,解答下列问题：
(1)当输入的$x$值为1时,输出的$y$值为
(2)求$k,b$的值；
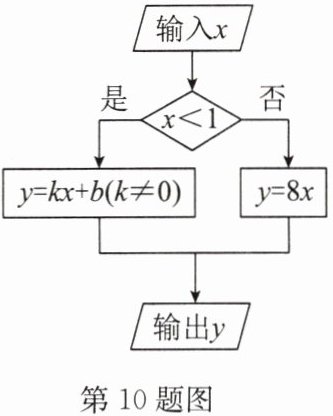
(3)当输出的$y$值为0时,求输入的$x$值.
根据以上信息,解答下列问题：
(1)当输入的$x$值为1时,输出的$y$值为
8
；(2)求$k,b$的值；
(3)当输出的$y$值为0时,求输入的$x$值.
(2)解:将(−2,2),(0,6)代入y=kx+b中, 得{2=-2k+b,6=b},解得{k=2,b=6}. (3)解:在y=8x中,令y=0,得0=8x,∴x=0＜1(不合题意，舍去). 由(2)得,y=2x+6,令y=0,得0=2x+6, 解得x=−3＜1.∴当输出的y值为0时，输入的x值为−3.
答案：
(1)8
(2)解:将(−2,2),(0,6)代入y=kx+b中, 得{2=-2k+b,6=b},解得{k=2,b=6}.
(3)解:在y=8x中,令y=0,得0=8x,
∴x=0＜1(不合题意，舍去). 由
(2)得,y=2x+6,令y=0,得0=2x+6, 解得x=−3＜1.
∴当输出的y值为0时，输入的x值为−3.
(1)8
(2)解:将(−2,2),(0,6)代入y=kx+b中, 得{2=-2k+b,6=b},解得{k=2,b=6}.
(3)解:在y=8x中,令y=0,得0=8x,
∴x=0＜1(不合题意，舍去). 由
(2)得,y=2x+6,令y=0,得0=2x+6, 解得x=−3＜1.
∴当输出的y值为0时，输入的x值为−3.
11. (20分)如图,已知B中的实数与A中的实数之间的对应关系是一次函数.若用$y$表示B中的实数,用$x$表示A中的实数,点$M的坐标为(n-m,t)$,点$N的坐标为(-m,0)$.
(1)求$y与x$之间的函数表达式；
(2)点$M,N$的坐标分别是______、______,线段$MN$的长度为______；
(3)若点$Q$在第二象限,且以$\triangle MNQ$的三条边的长度组成的数组是勾股数,请求出点$Q$的坐标(
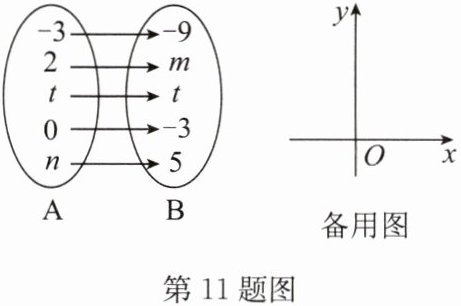
(1)求$y与x$之间的函数表达式；
(2)点$M,N$的坐标分别是______、______,线段$MN$的长度为______；
(3)若点$Q$在第二象限,且以$\triangle MNQ$的三条边的长度组成的数组是勾股数,请求出点$Q$的坐标(
写
出
一个
即
可
).答案：
(1)解:设y与x之间的函数表达式为y=kx+b(k≠0),把{x=-3,y=-9}和{x=0,y=-3}代入，得{-9=-3k+b,-3=b}, 解得{k=2,b=-3}.
∴y与x之间的函数表达式为y=2x−3.
(2)(3,3) (−1,0) 5
(3)解:如答图,QN⊥x轴,QM⊥y轴,且∠Q=90°.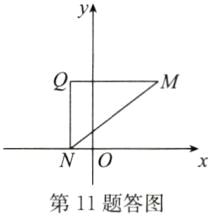
由M(3,3),N(−1,0)得Q(−1,3),此时QN=3,QM=4,MN=5,3,4,5正好是勾股数.
∴符合要求的点Q的坐标为(−1,3).
(1)解:设y与x之间的函数表达式为y=kx+b(k≠0),把{x=-3,y=-9}和{x=0,y=-3}代入，得{-9=-3k+b,-3=b}, 解得{k=2,b=-3}.
∴y与x之间的函数表达式为y=2x−3.
(2)(3,3) (−1,0) 5
(3)解:如答图,QN⊥x轴,QM⊥y轴,且∠Q=90°.
由M(3,3),N(−1,0)得Q(−1,3),此时QN=3,QM=4,MN=5,3,4,5正好是勾股数.∴符合要求的点Q的坐标为(−1,3).