1. 两个一次函数 $ y = ax + b $ 和 $ y = bx + a $ 在同一平面直角坐标系中的图象可能是(
]
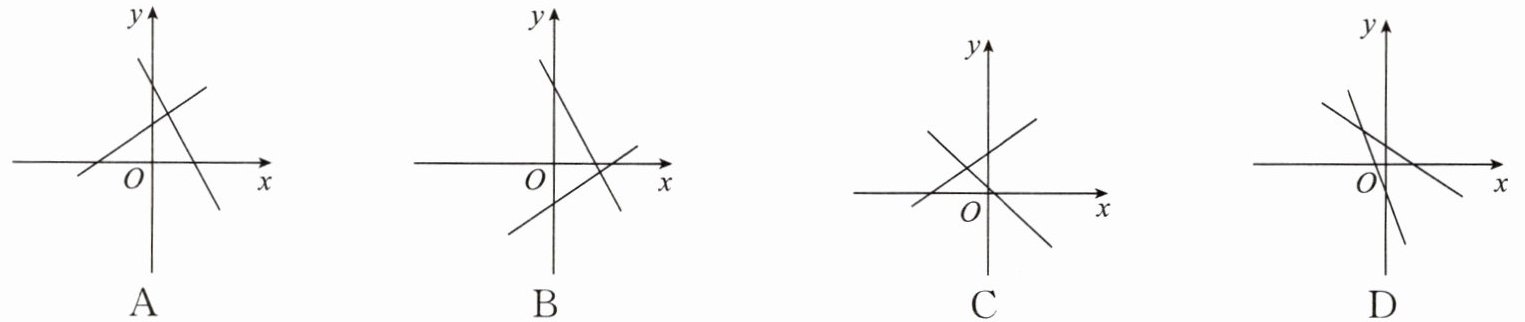
B
)]

答案:B
解析:
解:分情况讨论:
1. 当$a>0$,$b>0$时,$y=ax+b$过第一、二、三象限,$y=bx+a$过第一、二、三象限,无符合选项;
2. 当$a>0$,$b<0$时,$y=ax+b$过第一、三、四象限,$y=bx+a$过第一、二、四象限,选项B符合;
3. 当$a<0$,$b>0$时,$y=ax+b$过第一、二、四象限,$y=bx+a$过第一、三、四象限,无符合选项;
4. 当$a<0$,$b<0$时,$y=ax+b$过第二、三、四象限,$y=bx+a$过第二、三、四象限,无符合选项。
结论:B
1. 当$a>0$,$b>0$时,$y=ax+b$过第一、二、三象限,$y=bx+a$过第一、二、三象限,无符合选项;
2. 当$a>0$,$b<0$时,$y=ax+b$过第一、三、四象限,$y=bx+a$过第一、二、四象限,选项B符合;
3. 当$a<0$,$b>0$时,$y=ax+b$过第一、二、四象限,$y=bx+a$过第一、三、四象限,无符合选项;
4. 当$a<0$,$b<0$时,$y=ax+b$过第二、三、四象限,$y=bx+a$过第二、三、四象限,无符合选项。
结论:B
2. 一次函数 $ y = kx - 1(k \neq 0) $,若 $ y $ 随 $ x $ 的增大而减小,则它的图象不经过(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
A
)A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:A
解析:
∵一次函数$y = kx - 1(k \neq 0)$中$y$随$x$的增大而减小,
∴$k < 0$。
又
∵$b=-1 < 0$,
∴该函数图象经过第二、三、四象限,不经过第一象限。
A
3. (2024·宿迁共同体期末)已知点 $ (-2,y_1),(2,y_2) $ 都在直线 $ y = 2x - 3 $ 上,则 $ y_1 $
<
$ y_2 $.(填“$<$”“$>$”或“$=$”)答案:<
解析:
当$x=-2$时,$y_1=2×(-2)-3=-4 - 3=-7$;当$x=2$时,$y_2=2×2 - 3=4 - 3=1$。因为$-7<1$,所以$y_1<y_2$。
4. 直线 $ y = -2x + 8 $ 与两坐标轴围成的三角形的面积为
16
.答案:16
解析:
当$x=0$时,$y=-2×0 + 8=8$,直线与$y$轴交点坐标为$(0,8)$;当$y=0$时,$0=-2x + 8$,解得$x=4$,直线与$x$轴交点坐标为$(4,0)$。则直线与两坐标轴围成的三角形两直角边的长分别为$4$和$8$,面积为$\frac{1}{2}×4×8 = 16$。
16
16
5. 已知一次函数 $ y = (2m + 3)x + m - 1 $.
(1) 若该函数图象平行于直线 $ y = x + 1 $,求 $ m $ 的值;
(2) 若该函数的值 $ y $ 随自变量 $ x $ 的增大而减小,求 $ m $ 的取值范围;
(3) 该函数图象不经过第二象限,求 $ m $ 的取值范围.
(1) 若该函数图象平行于直线 $ y = x + 1 $,求 $ m $ 的值;
(2) 若该函数的值 $ y $ 随自变量 $ x $ 的增大而减小,求 $ m $ 的取值范围;
(3) 该函数图象不经过第二象限,求 $ m $ 的取值范围.
答案:解:
(1)
∵该函数图象平行于直线y=x+1,
∴2m+3=1,解得m=-1.
(2)
∵该函数的值y随自变量x的增大而减小,
∴2m+3<0,解得m<-$\frac{3}{2}$.
(3)
∵该函数图象不经过第二象限,
∴$\begin{cases}2m + 3 > 0\\m - 1 \leq 0\end{cases}$,解得-$\frac{3}{2}$<m≤1.
(1)
∵该函数图象平行于直线y=x+1,
∴2m+3=1,解得m=-1.
(2)
∵该函数的值y随自变量x的增大而减小,
∴2m+3<0,解得m<-$\frac{3}{2}$.
(3)
∵该函数图象不经过第二象限,
∴$\begin{cases}2m + 3 > 0\\m - 1 \leq 0\end{cases}$,解得-$\frac{3}{2}$<m≤1.
6. 若点 $ A(x_1,-3),B(x_2,-2),C(x_3,1) $ 均在一次函数 $ y = 3x - b $ 的图象上,则 $ x_1,x_2,x_3 $ 的大小关系是(
A.$ x_1 < x_2 < x_3 $
B.$ x_2 < x_1 < x_3 $
C.$ x_3 < x_2 < x_1 $
D.$ x_1 < x_3 < x_2 $
A
)A.$ x_1 < x_2 < x_3 $
B.$ x_2 < x_1 < x_3 $
C.$ x_3 < x_2 < x_1 $
D.$ x_1 < x_3 < x_2 $
答案:A
解析:
因为点$A(x_1,-3)$在$y = 3x - b$上,所以$-3=3x_1 - b$,解得$x_1=\frac{b - 3}{3}$。
因为点$B(x_2,-2)$在$y = 3x - b$上,所以$-2=3x_2 - b$,解得$x_2=\frac{b - 2}{3}$。
因为点$C(x_3,1)$在$y = 3x - b$上,所以$1=3x_3 - b$,解得$x_3=\frac{b + 1}{3}$。
因为$\frac{b - 3}{3}<\frac{b - 2}{3}<\frac{b + 1}{3}$,所以$x_1<x_2<x_3$。
A
因为点$B(x_2,-2)$在$y = 3x - b$上,所以$-2=3x_2 - b$,解得$x_2=\frac{b - 2}{3}$。
因为点$C(x_3,1)$在$y = 3x - b$上,所以$1=3x_3 - b$,解得$x_3=\frac{b + 1}{3}$。
因为$\frac{b - 3}{3}<\frac{b - 2}{3}<\frac{b + 1}{3}$,所以$x_1<x_2<x_3$。
A
7. 关于直线 $ l:y = kx + k(k \neq 0) $,下列说法中错误的是(
A.点 $ (0,k) $ 在直线 $ l $ 上
B.直线 $ l $ 经过定点 $ (-1,0) $
C.直线 $ l $ 经过第一、二、三象限
D.当 $ k > 0 $ 时,$ y $ 随 $ x $ 的增大而增大
C
)A.点 $ (0,k) $ 在直线 $ l $ 上
B.直线 $ l $ 经过定点 $ (-1,0) $
C.直线 $ l $ 经过第一、二、三象限
D.当 $ k > 0 $ 时,$ y $ 随 $ x $ 的增大而增大
答案:C
解析:
A. 当$x=0$时,$y=k×0 + k=k$,点$(0,k)$在直线$l$上,正确。
B. $y=kx + k=k(x + 1)$,当$x=-1$时,$y=0$,直线$l$经过定点$(-1,0)$,正确。
C. 当$k\lt0$时,$k\lt0$,$b=k\lt0$,直线经过第二、三、四象限,错误。
D. 当$k\gt0$时,$y$随$x$的增大而增大,正确。
结论:C
B. $y=kx + k=k(x + 1)$,当$x=-1$时,$y=0$,直线$l$经过定点$(-1,0)$,正确。
C. 当$k\lt0$时,$k\lt0$,$b=k\lt0$,直线经过第二、三、四象限,错误。
D. 当$k\gt0$时,$y$随$x$的增大而增大,正确。
结论:C
8. 已知一次函数 $ y = (k + 3)x + k - 2 $,$ y $ 随 $ x $ 的增大而增大,且该函数图象与 $ y $ 轴交于负半轴,则 $ k $ 的取值范围是
-3<k<2
.答案:-3<k<2
解析:
解:因为一次函数$y=(k + 3)x + k - 2$,$y$随$x$的增大而增大,所以$k + 3>0$,解得$k>-3$;
又因为该函数图象与$y$轴交于负半轴,所以当$x=0$时,$y=k - 2<0$,解得$k<2$;
综上,$k$的取值范围是$-3 < k < 2$。
又因为该函数图象与$y$轴交于负半轴,所以当$x=0$时,$y=k - 2<0$,解得$k<2$;
综上,$k$的取值范围是$-3 < k < 2$。
9. (2024·自贡)一次函数 $ y = (3m + 1)x - 2 $ 的函数值随 $ x $ 的增大而增大,请写出一个满足条件的 $ m $ 的值:
1(答案不唯一)
.答案:1(答案不唯一)