10. 已知直线 $ l_1:y = 2x - 6 $,则直线 $ l_1 $ 关于 $ x $ 轴对称的直线 $ l_2 $ 的函数表达式是
y=-2x+6
.答案:y=-2x+6
解析:
在直线$l_1:y = 2x - 6$上取两点,当$x=0$时,$y=-6$,得点$(0,-6)$;当$y=0$时,$2x - 6=0$,解得$x=3$,得点$(3,0)$。
点$(0,-6)$关于$x$轴对称的点为$(0,6)$,点$(3,0)$关于$x$轴对称的点仍为$(3,0)$。
设直线$l_2$的函数表达式为$y=kx + b$,将$(0,6)$和$(3,0)$代入得:$\begin{cases}b=6\\3k + b=0\end{cases}$,解得$\begin{cases}k=-2\\b=6\end{cases}$。
所以直线$l_2$的函数表达式是$y=-2x + 6$。
点$(0,-6)$关于$x$轴对称的点为$(0,6)$,点$(3,0)$关于$x$轴对称的点仍为$(3,0)$。
设直线$l_2$的函数表达式为$y=kx + b$,将$(0,6)$和$(3,0)$代入得:$\begin{cases}b=6\\3k + b=0\end{cases}$,解得$\begin{cases}k=-2\\b=6\end{cases}$。
所以直线$l_2$的函数表达式是$y=-2x + 6$。
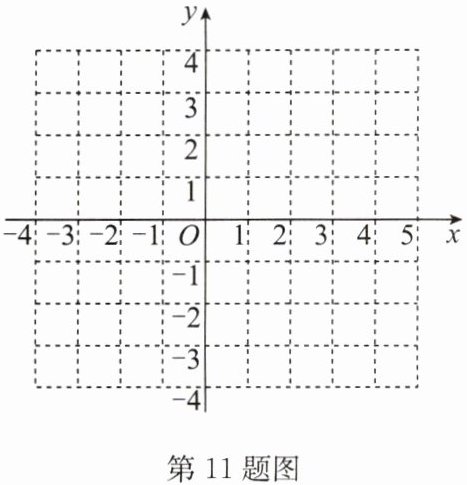
11. 如图,在平面直角坐标系中画出一次函数 $ y = 2x - 4 $ 的图象,并完成下列问题:
(1) 此函数图象与坐标轴围成的三角形的面积是______;
(2) 观察图象,当 $ 0 \leq x \leq 4 $ 时,$ y $ 的取值范围是______;
(3) 若直线 $ y = 2x - 4 $ 平移后经过点 $ (-3,1) $,求平移后的直线的函数表达式.
(1) 此函数图象与坐标轴围成的三角形的面积是______;
(2) 观察图象,当 $ 0 \leq x \leq 4 $ 时,$ y $ 的取值范围是______;
(3) 若直线 $ y = 2x - 4 $ 平移后经过点 $ (-3,1) $,求平移后的直线的函数表达式.

答案:
画图如答图所示.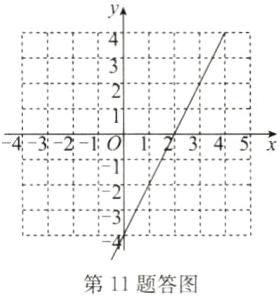
(1)4
(2)-4≤y≤4
(3)解:设平移后的直线的函数表达式为y=2x+b,将(-3,1)代入,得b=7,
∴平移后的直线的函数表达式为y=2x+7.
画图如答图所示.

(1)4
(2)-4≤y≤4
(3)解:设平移后的直线的函数表达式为y=2x+b,将(-3,1)代入,得b=7,
∴平移后的直线的函数表达式为y=2x+7.
12. 如图,已知直线 $ y = 2x + 3 $,点 $ A(a,0) $ 为 $ x $ 轴上一个动点,过点 $ A $ 作 $ x $ 轴的垂线,交直线 $ y = 2x + 3 $ 于点 $ B $,若线段 $ AB = 5 $,求 $ a $ 的值.
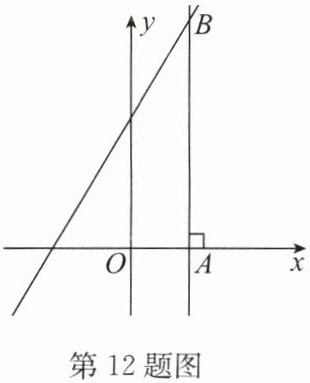

答案:解:由题意得,点B的横坐标为a,则纵坐标为2a+3,
∴AB=|2a+3|=5,解得a=1或a=-4,
∴a的值为1或-4.
∴AB=|2a+3|=5,解得a=1或a=-4,
∴a的值为1或-4.
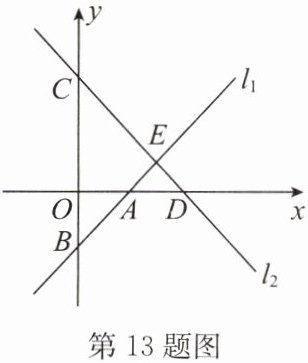
13. 如图,已知直线 $ l_1:y = kx - 2 $ 与直线 $ y = x $ 平行,与 $ x $ 轴交于点 $ A $,与 $ y $ 轴交于点 $ B $,直线 $ l_2 $ 与 $ y $ 轴交于点 $ C(0,4) $,与 $ x $ 轴交于点 $ D $,与直线 $ l_1 $ 交于点 $ E(3,m) $.
(1) 求直线 $ l_2 $ 对应的函数表达式;
(2) 求四边形 $ AOCE $ 的面积.
(1) 求直线 $ l_2 $ 对应的函数表达式;
(2) 求四边形 $ AOCE $ 的面积.

答案:解:
(1)
∵直线l₁:y=kx-2与直线y=x平行,
∴k=1,
∴l₁:y=x-2,
∴A(2,0).
∵点E(3,m)在直线l₁上,
∴m=1,
∴点E(3,1).
∵直线l₂与y轴交于点C(0,4),且过点E,
∴设直线l₂的函数表达式为y=ax+4,则1=3a+4,解得a=-1.
∴直线l₂对应的函数表达式为y=-x+4.
(2)易知D(4,0),从而OC=OD=4,AD=2.
∴S四边形AOCE=S△OCD-S△AED=$\frac{1}{2}$OC·OD-$\frac{1}{2}$AD·|y_E|=$\frac{1}{2}$×4×4-$\frac{1}{2}$×2×1=8-1=7.
(1)
∵直线l₁:y=kx-2与直线y=x平行,
∴k=1,
∴l₁:y=x-2,
∴A(2,0).
∵点E(3,m)在直线l₁上,
∴m=1,
∴点E(3,1).
∵直线l₂与y轴交于点C(0,4),且过点E,
∴设直线l₂的函数表达式为y=ax+4,则1=3a+4,解得a=-1.
∴直线l₂对应的函数表达式为y=-x+4.
(2)易知D(4,0),从而OC=OD=4,AD=2.
∴S四边形AOCE=S△OCD-S△AED=$\frac{1}{2}$OC·OD-$\frac{1}{2}$AD·|y_E|=$\frac{1}{2}$×4×4-$\frac{1}{2}$×2×1=8-1=7.