1. 某登山队大本营所在地的气温为 $ 8^{\circ}C $。海拔每升高 $ 1km $,气温下降 $ 6^{\circ}C $。队员由大本营向上登高 $ xkm $,气温为 $ y^{\circ}C $,则 $ y $ 与 $ x $ 的函数关系式为(
A.$ y = 8 + 6x $
B.$ y = 8 - 6x $
C.$ y = 6 - \frac{3}{4}x $
D.$ y = 8 - \frac{3}{4}x $
B
)A.$ y = 8 + 6x $
B.$ y = 8 - 6x $
C.$ y = 6 - \frac{3}{4}x $
D.$ y = 8 - \frac{3}{4}x $
答案:B
解析:
由题意得,大本营气温为$8^{\circ}C$,海拔每升高$1km$气温下降$6^{\circ}C$,登高$xkm$,气温下降$6x^{\circ}C$,则气温$y = 8 - 6x$。
B
B
2. (2024·上海)某种商品的销售额 $ y $(万元)与广告投入 $ x $(万元)成一次函数关系. 当投入 $ 10 $ 万元时,销售额为 $ 1000 $ 万元;当投入 $ 90 $ 万元时,销售额为 $ 5000 $ 万元. 则投入 $ 80 $ 万元时,销售额为
4500
万元.答案:4500
解析:
设该一次函数为$y=kx+b$($k\neq0$)。
将$x=10$,$y=1000$和$x=90$,$y=5000$分别代入函数,得:
$\begin{cases}10k + b = 1000 \\90k + b = 5000\end{cases}$
用第二个方程减去第一个方程消去$b$:
$(90k + b) - (10k + b) = 5000 - 1000$
$80k = 4000$
解得$k = 50$。
将$k = 50$代入$10k + b = 1000$:
$10×50 + b = 1000$
$500 + b = 1000$
解得$b = 500$。
所以函数关系式为$y = 50x + 500$。
当$x = 80$时,$y = 50×80 + 500 = 4000 + 500 = 4500$。
4500
将$x=10$,$y=1000$和$x=90$,$y=5000$分别代入函数,得:
$\begin{cases}10k + b = 1000 \\90k + b = 5000\end{cases}$
用第二个方程减去第一个方程消去$b$:
$(90k + b) - (10k + b) = 5000 - 1000$
$80k = 4000$
解得$k = 50$。
将$k = 50$代入$10k + b = 1000$:
$10×50 + b = 1000$
$500 + b = 1000$
解得$b = 500$。
所以函数关系式为$y = 50x + 500$。
当$x = 80$时,$y = 50×80 + 500 = 4000 + 500 = 4500$。
4500
3. 已知池中有 $ 600m^{3} $ 的水,每小时抽 $ 50m^{3} $,则剩余水的体积 $ Q(m^{3}) $ 与时间 $ t(h) $ 的函数关系式是
Q=-50t+600(0≤t≤12)
.(写出自变量的取值范围)答案:Q=-50t+600(0≤t≤12)
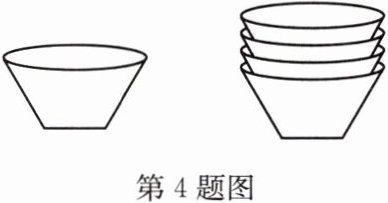
4. (2024·包头)如图是 $ 1 $ 个碗和 $ 4 $ 个整齐叠放成一摞的碗的示意图,碗的规格都是相同的. 小亮尝试结合学习函数的经验,探究整齐叠放成一摞的这种规格的碗的总高度 $ y $(单位:$ cm $)随着碗的数量 $ x $(单位:个)的变化规律. 下表是小亮经过测量得到的 $ y $ 与 $ x $ 之间的对应数据:

(1)依据小亮测量的数据,写出 $ y $ 与 $ x $ 之间的函数表达式,并说明理由;
(2)若整齐叠放成一摞的这种规格的碗的总高度不超过 $ 28.8cm $,求此时碗最多有多少个?

(1)依据小亮测量的数据,写出 $ y $ 与 $ x $ 之间的函数表达式,并说明理由;
(2)若整齐叠放成一摞的这种规格的碗的总高度不超过 $ 28.8cm $,求此时碗最多有多少个?

答案:
(1)由表中的数据知,x的增加量不变,
∴y是x的一次函数,设y=kx+b.由题意得:{k+b=6,2k+b=8.4,解得:{k=2.4,b=3.6,
∴y与x之间的函数表达式为y=2.4x+3.6.
(2)设碗有x个,则2.4x+3.6≤28.8,解得x≤10.5,
∴x的最大整数解为10.答:碗最多有10个.
(1)由表中的数据知,x的增加量不变,
∴y是x的一次函数,设y=kx+b.由题意得:{k+b=6,2k+b=8.4,解得:{k=2.4,b=3.6,
∴y与x之间的函数表达式为y=2.4x+3.6.
(2)设碗有x个,则2.4x+3.6≤28.8,解得x≤10.5,
∴x的最大整数解为10.答:碗最多有10个.
5. 已知某汽车油箱中的剩余油量 $ y $(升)与该汽车行驶里程数 $ x $(千米)是一次函数关系. 汽车加满油后,行驶 $ 100 $ 千米,油箱中还剩油 $ 38 $ 升;行驶 $ 150 $ 千米,油箱中还剩油 $ 32 $ 升. 那么,当这辆汽车行驶 $ 350 $ 千米时,油箱中还剩油
8
升.答案:8
解析:
设该一次函数为$y=kx+b$。
将$x=100$,$y=38$和$x=150$,$y=32$代入函数,得:
$\begin{cases}100k + b = 38 \\150k + b = 32\end{cases}$
用第二个方程减去第一个方程:
$(150k + b) - (100k + b) = 32 - 38$
$50k = -6$
$k = -\frac{6}{50} = -\frac{3}{25}$
将$k=-\frac{3}{25}$代入$100k + b = 38$:
$100×(-\frac{3}{25}) + b = 38$
$-12 + b = 38$
$b = 50$
所以函数关系式为$y = -\frac{3}{25}x + 50$。
当$x=350$时:
$y = -\frac{3}{25}×350 + 50 = -42 + 50 = 8$
8
将$x=100$,$y=38$和$x=150$,$y=32$代入函数,得:
$\begin{cases}100k + b = 38 \\150k + b = 32\end{cases}$
用第二个方程减去第一个方程:
$(150k + b) - (100k + b) = 32 - 38$
$50k = -6$
$k = -\frac{6}{50} = -\frac{3}{25}$
将$k=-\frac{3}{25}$代入$100k + b = 38$:
$100×(-\frac{3}{25}) + b = 38$
$-12 + b = 38$
$b = 50$
所以函数关系式为$y = -\frac{3}{25}x + 50$。
当$x=350$时:
$y = -\frac{3}{25}×350 + 50 = -42 + 50 = 8$
8
6. 和谐号动车刹车后做匀减速运动,速度 $ v(km/min) $ 与刹车时间 $ t(min) $ 之间满足函数关系式 $ v = -\frac{5}{4}t + 5 $. 动车在匀变速直线运动中,从开始刹车到准确停到站台,需要
4
$ min $.答案:4
解析:
当动车停止时,速度$v = 0$,则有:
$0 = -\frac{5}{4}t + 5$
$\frac{5}{4}t = 5$
$t = 5 × \frac{4}{5} = 4$
4
$0 = -\frac{5}{4}t + 5$
$\frac{5}{4}t = 5$
$t = 5 × \frac{4}{5} = 4$
4