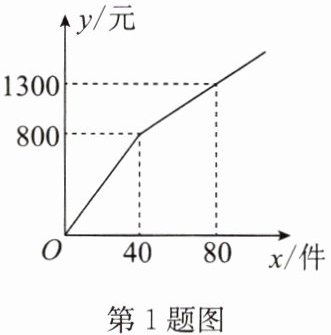
1. 某商店销售一种商品,售出部分商品后进行了降价促销,销售价格 $ y $(元)与销售量 $ x $(件)的函数关系如图所示,则降价后每件商品的销售价格为(
A.12 元
B.12.5 元
C.16.25 元
D.20 元
B
)
A.12 元
B.12.5 元
C.16.25 元
D.20 元
答案:B
解析:
解:由图可知,降价后销售量从40件增加到80件,销售额从800元增加到1300元。
降价后销售的商品数量为:$80 - 40 = 40$(件)
降价后增加的销售额为:$1300 - 800 = 500$(元)
降价后每件商品的销售价格为:$\frac{500}{40} = 12.5$(元)
B
降价后销售的商品数量为:$80 - 40 = 40$(件)
降价后增加的销售额为:$1300 - 800 = 500$(元)
降价后每件商品的销售价格为:$\frac{500}{40} = 12.5$(元)
B
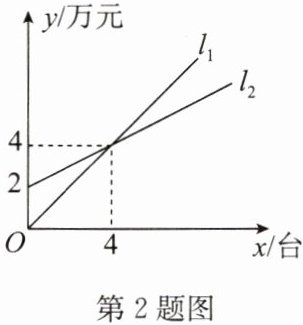
2. 如图,$ l_1 $ 表示某商场一天的手提电脑销售额与销售量的关系,$ l_2 $ 表示该商场一天的手提电脑销售成本与销售量的关系,则一天销售
8
台时,销售额比销售成本多 2 万元.
答案:8
解析:
解:设$ l_1 $的解析式为$ y_1 = k_1x $,将$(4,4)$代入得$ 4 = 4k_1 $,解得$ k_1 = 1 $,故$ y_1 = x $。
设$ l_2 $的解析式为$ y_2 = k_2x + b $,将$(0,2)$,$(4,4)$代入得$\begin{cases} b = 2 \\ 4 = 4k_2 + 2 \end{cases}$,解得$\begin{cases} k_2 = \frac{1}{2} \\ b = 2 \end{cases}$,故$ y_2 = \frac{1}{2}x + 2 $。
由题意得$ y_1 - y_2 = 2 $,即$ x - (\frac{1}{2}x + 2) = 2 $,解得$ x = 8 $。
8
设$ l_2 $的解析式为$ y_2 = k_2x + b $,将$(0,2)$,$(4,4)$代入得$\begin{cases} b = 2 \\ 4 = 4k_2 + 2 \end{cases}$,解得$\begin{cases} k_2 = \frac{1}{2} \\ b = 2 \end{cases}$,故$ y_2 = \frac{1}{2}x + 2 $。
由题意得$ y_1 - y_2 = 2 $,即$ x - (\frac{1}{2}x + 2) = 2 $,解得$ x = 8 $。
8
3. 某市某医药公司把一批药品运往外地,现有两种运输方式可供选择.
方式一:使用汽车运输,装卸收费 400 元,另外每千米再加收 4 元;
方式二:使用火车运输,装卸收费 820 元,另外每千米再加收 2 元.
(1) 请分别写出用汽车、火车运输的总费用 $ y_1 $(元),$ y_2 $(元)与运输路程 $ x $(km) 之间的函数关系式;
(2) 你认为选用哪种运输方式更省钱?
方式一:使用汽车运输,装卸收费 400 元,另外每千米再加收 4 元;
方式二:使用火车运输,装卸收费 820 元,另外每千米再加收 2 元.
(1) 请分别写出用汽车、火车运输的总费用 $ y_1 $(元),$ y_2 $(元)与运输路程 $ x $(km) 之间的函数关系式;
(2) 你认为选用哪种运输方式更省钱?
答案:解:
(1)由题意,得$y_{1}=4x+400$;$y_{2}=2x+820$.
(2)若$4x+400=2x+820$,则$x=210$.
故运输路程小于 210 km 时,$y_{1}\lt y_{2}$,选择用汽车运输更省钱;
运输路程等于 210 km 时,$y_{1}=y_{2}$,两种运输方式一样;
运输路程大于 210 km 时,$y_{1}\gt y_{2}$,选择用火车运输更省钱.
(1)由题意,得$y_{1}=4x+400$;$y_{2}=2x+820$.
(2)若$4x+400=2x+820$,则$x=210$.
故运输路程小于 210 km 时,$y_{1}\lt y_{2}$,选择用汽车运输更省钱;
运输路程等于 210 km 时,$y_{1}=y_{2}$,两种运输方式一样;
运输路程大于 210 km 时,$y_{1}\gt y_{2}$,选择用火车运输更省钱.
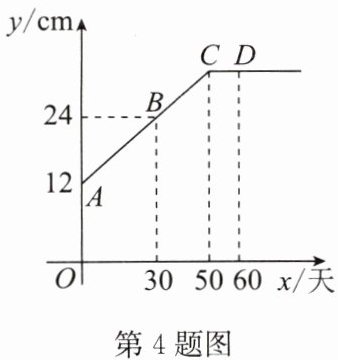
4. (2024·徐州一模) 莴笋是一种营养价值极高的蔬菜. 实践小组观察记录了莴笋的生长过程,下图表示莴笋苗的生长高度 $ y $(cm) 与观察时间 $ x $(天) 的函数图象,则莴笋生长的最大高度是(
A.25 cm
B.32 cm
C.35 cm
D.40 cm
B
)
A.25 cm
B.32 cm
C.35 cm
D.40 cm
答案:B
解析:
解:设AB段的函数解析式为$y = kx + b$。
将$A(0,12)$,$B(30,24)$代入得:
$\begin{cases}b = 12 \\30k + b = 24\end{cases}$
解得$k = \frac{12}{30} = 0.4$,$b = 12$,所以$y = 0.4x + 12$。
当$x = 50$时,$y = 0.4×50 + 12 = 32$。
由图象知CD段高度不变,故最大高度为32 cm。
B
将$A(0,12)$,$B(30,24)$代入得:
$\begin{cases}b = 12 \\30k + b = 24\end{cases}$
解得$k = \frac{12}{30} = 0.4$,$b = 12$,所以$y = 0.4x + 12$。
当$x = 50$时,$y = 0.4×50 + 12 = 32$。
由图象知CD段高度不变,故最大高度为32 cm。
B
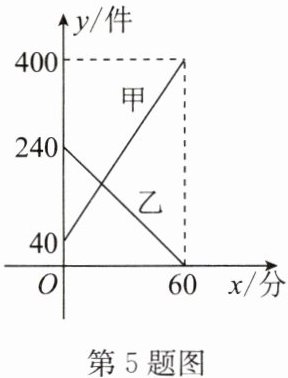
5. (2024·淮安一模) 某快递公司每天上午 9:00~10:00 为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量 $ y $(件) 与时间 $ x $(分) 之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为(
A.9:15
B.9:20
C.9:25
D.9:30
B
)
A.9:15
B.9:20
C.9:25
D.9:30
答案:B
解析:
解:设甲仓库的函数解析式为$y=k_1x+b_1$,将$(0,40)$,$(60,400)$代入得:
$\begin{cases}b_1=40 \\60k_1+b_1=400\end{cases}$
解得$k_1=6$,$b_1=40$,故$y=6x+40$。
设乙仓库的函数解析式为$y=k_2x+b_2$,将$(0,240)$,$(60,0)$代入得:
$\begin{cases}b_2=240 \\60k_2+b_2=0\end{cases}$
解得$k_2=-4$,$b_2=240$,故$y=-4x+240$。
令$6x+40=-4x+240$,解得$x=20$。
此刻时间为9:20。
B
$\begin{cases}b_1=40 \\60k_1+b_1=400\end{cases}$
解得$k_1=6$,$b_1=40$,故$y=6x+40$。
设乙仓库的函数解析式为$y=k_2x+b_2$,将$(0,240)$,$(60,0)$代入得:
$\begin{cases}b_2=240 \\60k_2+b_2=0\end{cases}$
解得$k_2=-4$,$b_2=240$,故$y=-4x+240$。
令$6x+40=-4x+240$,解得$x=20$。
此刻时间为9:20。
B