1. 给出下面四条直线,其中直线上每个点的坐标都是二元一次方程 $x - 2y = 2$ 的解的是(

C
)
答案:C
解析:
解:将方程$x - 2y = 2$变形为$y=\frac{1}{2}x - 1$。
当$x=0$时,$y=-1$,直线与$y$轴交于点$(0,-1)$;
当$y=0$时,$x=2$,直线与$x$轴交于点$(2,0)$。
观察图像,只有选项C的直线经过$(0,-1)$和$(2,0)$。
答案:C
当$x=0$时,$y=-1$,直线与$y$轴交于点$(0,-1)$;
当$y=0$时,$x=2$,直线与$x$轴交于点$(2,0)$。
观察图像,只有选项C的直线经过$(0,-1)$和$(2,0)$。
答案:C
2. 直线 $y = ax + b(a \neq 0)$ 过点 $A(0,1)$,$B(2,0)$,则关于 $x$ 的方程 $ax + b = 0$ 的解为(
A.$x = 0$
B.$x = 1$
C.$x = 2$
D.$x = 3$
C
)A.$x = 0$
B.$x = 1$
C.$x = 2$
D.$x = 3$
答案:C
解析:
方程$ax + b = 0$的解为直线$y = ax + b$与$x$轴交点的横坐标。
已知直线过点$B(2,0)$,即直线与$x$轴交点为$(2,0)$。
因此,方程$ax + b = 0$的解为$x = 2$。
C
已知直线过点$B(2,0)$,即直线与$x$轴交点为$(2,0)$。
因此,方程$ax + b = 0$的解为$x = 2$。
C
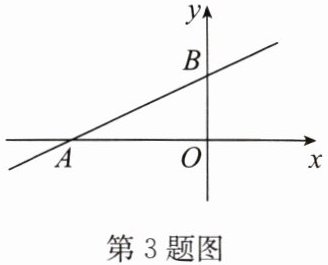
3. (2024·扬州)如图,已知一次函数 $y = kx + b(k \neq 0)$ 的图象分别与 $x$ 轴、$y$ 轴交于 $A$,$B$ 两点,若 $OA = 2$,$OB = 1$,则关于 $x$ 的方程 $kx + b = 0$ 的解为
x=-2
.
答案:x=-2
解析:
解:
∵一次函数$y = kx + b(k \neq 0)$的图象与$x$轴交于点$A$,$OA = 2$,
∴点$A$的坐标为$(-2, 0)$或$(2, 0)$。
又
∵函数图象与$y$轴交于点$B$,$OB = 1$,结合图象可知点$B$在$y$轴正半轴,即$b>0$,且函数图象从左到右上升,$k>0$,此时点$A$在$x$轴负半轴,
∴点$A$的坐标为$(-2, 0)$。
∵关于$x$的方程$kx + b = 0$的解为一次函数$y = kx + b$的图象与$x$轴交点的横坐标,
∴方程$kx + b = 0$的解为$x=-2$。
$x=-2$
∵一次函数$y = kx + b(k \neq 0)$的图象与$x$轴交于点$A$,$OA = 2$,
∴点$A$的坐标为$(-2, 0)$或$(2, 0)$。
又
∵函数图象与$y$轴交于点$B$,$OB = 1$,结合图象可知点$B$在$y$轴正半轴,即$b>0$,且函数图象从左到右上升,$k>0$,此时点$A$在$x$轴负半轴,
∴点$A$的坐标为$(-2, 0)$。
∵关于$x$的方程$kx + b = 0$的解为一次函数$y = kx + b$的图象与$x$轴交点的横坐标,
∴方程$kx + b = 0$的解为$x=-2$。
$x=-2$
4. 已知关于 $x$,$y$ 的二元一次方程组 $\begin{cases}ax - y + b = 0, \\ x + y + 5 = 0\end{cases} $ 的解是 $\begin{cases}x = -3, \\ y = -2,\end{cases} $ 则一次函数 $y = ax + b$ 和 $y = -x - 5$ 的图象的交点坐标为
(-3,-2)
.答案:(-3,-2)
5. 如图,利用图象法解二元一次方程组:$\begin{cases}y = -x + 5, \\ y = 2x - 1.\end{cases} $


答案:
解:如答图,作一次函数y=-x+5和y=2x-1的图象,交点为P(2,3),故二元一次方程组:$\left\{\begin{array}{l} y=-x+5\\ y=2x-1\end{array}\right. $的解为$\left\{\begin{array}{l} x=2\\ y=3\end{array}\right. $.

解:如答图,作一次函数y=-x+5和y=2x-1的图象,交点为P(2,3),故二元一次方程组:$\left\{\begin{array}{l} y=-x+5\\ y=2x-1\end{array}\right. $的解为$\left\{\begin{array}{l} x=2\\ y=3\end{array}\right. $.

6. (2024·呼伦贝尔)点 $P(x,y)$ 在直线 $y = -\frac{3}{4}x + 4$ 上,坐标 $(x,y)$ 是二元一次方程 $5x - 6y = 33$ 的解,则点 $P$ 的位置在(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
D
)A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:D
解析:
因为点$P(x,y)$在直线$y = -\frac{3}{4}x + 4$上,且坐标$(x,y)$是二元一次方程$5x - 6y = 33$的解,所以可得方程组:
$\begin{cases}y = -\frac{3}{4}x + 4 \\5x - 6y = 33\end{cases}$
将$y = -\frac{3}{4}x + 4$代入$5x - 6y = 33$中,得:
$5x - 6\left(-\frac{3}{4}x + 4\right) = 33$
$5x + \frac{9}{2}x - 24 = 33$
$\frac{10}{2}x + \frac{9}{2}x = 33 + 24$
$\frac{19}{2}x = 57$
$x = 57×\frac{2}{19} = 6$
将$x = 6$代入$y = -\frac{3}{4}x + 4$,得:
$y = -\frac{3}{4}×6 + 4 = -\frac{9}{2} + 4 = -\frac{1}{2}$
所以点$P$的坐标为$(6, -\frac{1}{2})$,在第四象限。
D
$\begin{cases}y = -\frac{3}{4}x + 4 \\5x - 6y = 33\end{cases}$
将$y = -\frac{3}{4}x + 4$代入$5x - 6y = 33$中,得:
$5x - 6\left(-\frac{3}{4}x + 4\right) = 33$
$5x + \frac{9}{2}x - 24 = 33$
$\frac{10}{2}x + \frac{9}{2}x = 33 + 24$
$\frac{19}{2}x = 57$
$x = 57×\frac{2}{19} = 6$
将$x = 6$代入$y = -\frac{3}{4}x + 4$,得:
$y = -\frac{3}{4}×6 + 4 = -\frac{9}{2} + 4 = -\frac{1}{2}$
所以点$P$的坐标为$(6, -\frac{1}{2})$,在第四象限。
D