11.(15 分)已知一次函数 $ y = kx + b $ 的图象经过点 $ (-2,4) $,且与正比例函数 $ y = 2x $ 的图象平行.
(1) 求一次函数 $ y = kx + b $ 的表达式;
(2) 求一次函数 $ y = kx + b $ 的图象与坐标轴所围成的三角形的面积.
(1) 求一次函数 $ y = kx + b $ 的表达式;
(2) 求一次函数 $ y = kx + b $ 的图象与坐标轴所围成的三角形的面积.
答案:解:
(1)
∵一次函数y=kx+b的图象与正比例函数y=2x的图象平行,
∴k=2.
∵一次函数y=kx+b的图象经过点(-2,4),
∴-2×2+b=4,解得b=8.
∴一次函数y=kx+b的表达式为y=2x+8.
(2)在y=2x+8中,令x=0,得y=8;令y=0,得x=-4,
∴直线y=2x+8与x轴、y轴分别相交于点A(-4,0),B(0,8).
∴一次函数y=kx+b的图象与坐标轴所围成的三角形的面积为$\frac{1}{2}OA\cdot OB=\frac{1}{2}×4×8=16$.
(1)
∵一次函数y=kx+b的图象与正比例函数y=2x的图象平行,
∴k=2.
∵一次函数y=kx+b的图象经过点(-2,4),
∴-2×2+b=4,解得b=8.
∴一次函数y=kx+b的表达式为y=2x+8.
(2)在y=2x+8中,令x=0,得y=8;令y=0,得x=-4,
∴直线y=2x+8与x轴、y轴分别相交于点A(-4,0),B(0,8).
∴一次函数y=kx+b的图象与坐标轴所围成的三角形的面积为$\frac{1}{2}OA\cdot OB=\frac{1}{2}×4×8=16$.
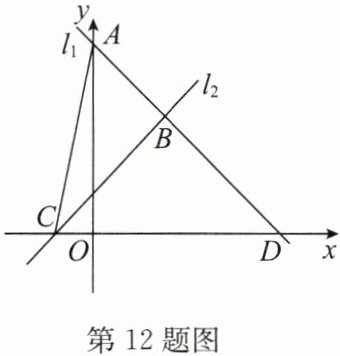
12.(15 分)如图,一次函数 $ y = kx + b(k \neq 0) $ 的图象为直线 $ l_1 $ 且经过 $ A(0,5) $ 和 $ D(5,0) $ 两点,一次函数 $ y = x + 1 $ 的图象为直线 $ l_2 $,与 $ x $ 轴交于点 $ C $,连接 $ AC $,两直线 $ l_1 $,$ l_2 $ 相交于点 $ B $.
(1) 求 $ k $,$ b $ 的值;
(2) 求点 $ B $ 的坐标;
(3) 求 $ \triangle ABC $ 的面积.
(1) 求 $ k $,$ b $ 的值;
(2) 求点 $ B $ 的坐标;
(3) 求 $ \triangle ABC $ 的面积.

答案:解:
(1)把(0,5)和(5,0)代入y=kx+b,得$\begin{cases}5k+b=0,\\b=5,\end{cases}$解得$\begin{cases}k=-1,\\b=5.\end{cases}$
(2)由
(1)得直线$l_1$的函数表达式为y=-x+5,联立直线$l_1$,$l_2$的函数表达式得$\begin{cases}y=-x+5,\\y=x+1,\end{cases}$解得$\begin{cases}x=2,\\y=3,\end{cases}$
∴B(2,3).
(3)由y=x+1知,当y=0时,x+1=0,解得x=-1,
∴点C(-1,0),
∴$S_{\triangle ABC}=S_{\triangle ACD}-S_{\triangle BCD}=\frac{1}{2}×6×5-\frac{1}{2}×6×3=6$.
(1)把(0,5)和(5,0)代入y=kx+b,得$\begin{cases}5k+b=0,\\b=5,\end{cases}$解得$\begin{cases}k=-1,\\b=5.\end{cases}$
(2)由
(1)得直线$l_1$的函数表达式为y=-x+5,联立直线$l_1$,$l_2$的函数表达式得$\begin{cases}y=-x+5,\\y=x+1,\end{cases}$解得$\begin{cases}x=2,\\y=3,\end{cases}$
∴B(2,3).
(3)由y=x+1知,当y=0时,x+1=0,解得x=-1,
∴点C(-1,0),
∴$S_{\triangle ABC}=S_{\triangle ACD}-S_{\triangle BCD}=\frac{1}{2}×6×5-\frac{1}{2}×6×3=6$.
13.(20 分)(2024·达州)为拓宽销售渠道,助力乡村振兴,某乡镇帮助农户将 A,B 两个品种的柑橘加工包装成礼盒再出售. 已知每件 A 品种柑橘礼盒比 B 品种柑橘礼盒的售价少 20 元,且出售 25 件 A 品种柑橘礼盒和 15 件 B 品种柑橘礼盒的总价为 3500 元.
(1) A,B 两种柑橘礼盒每件的售价分别为多少元?
(2) 已知加工 A,B 两种柑橘礼盒每件的成本分别为 50 元、60 元,该乡镇计划在某农产品展销活动中售出 A,B 两种柑橘礼盒共 1000 盒,且 A 品种柑橘礼盒售出的数量不超过 B 品种柑橘礼盒数量的 1.5 倍,总成本不超过 54050 元,要使农户收益最大,该乡镇应怎样安排 A,B 两种柑橘礼盒的销售方案?并求出农户在这次农产品展销活动中的最大收益.
(1) A,B 两种柑橘礼盒每件的售价分别为多少元?
(2) 已知加工 A,B 两种柑橘礼盒每件的成本分别为 50 元、60 元,该乡镇计划在某农产品展销活动中售出 A,B 两种柑橘礼盒共 1000 盒,且 A 品种柑橘礼盒售出的数量不超过 B 品种柑橘礼盒数量的 1.5 倍,总成本不超过 54050 元,要使农户收益最大,该乡镇应怎样安排 A,B 两种柑橘礼盒的销售方案?并求出农户在这次农产品展销活动中的最大收益.
答案:解:
(1)设A品种柑橘礼盒每件的售价为x元,则B品种柑橘礼盒每件的售价为(x+20)元.由题意得25x+15(x+20)=3500,解得x=80,
∴x+20=100.答:A品种柑橘礼盒每件的售价为80元,B品种柑橘礼盒每件的售价为100元.
(2)设销售A品种柑橘礼盒m盒,则销售B品种柑橘礼盒(1000-m)盒.由题意得$\begin{cases}m\leq1.5(1000-m),\\50m+60(1000-m)\leq54050,\end{cases}$解得595≤m≤600.设收益为w元,由题意得w=(80-50)m+(100-60)(1000-m)=-10m+40000.
∵-10<0,
∴w随m的增大而减小,
∴当m=595时,w取得最大值,最大值为-10×595+40000=34050,此时,1000-m=1000-595=405.答:使农户收益最大,应该安排销售A品种柑橘礼盒595盒,B品种柑橘礼盒405盒,农户在这次农产品展销活动中的最大收益为34050元.
(1)设A品种柑橘礼盒每件的售价为x元,则B品种柑橘礼盒每件的售价为(x+20)元.由题意得25x+15(x+20)=3500,解得x=80,
∴x+20=100.答:A品种柑橘礼盒每件的售价为80元,B品种柑橘礼盒每件的售价为100元.
(2)设销售A品种柑橘礼盒m盒,则销售B品种柑橘礼盒(1000-m)盒.由题意得$\begin{cases}m\leq1.5(1000-m),\\50m+60(1000-m)\leq54050,\end{cases}$解得595≤m≤600.设收益为w元,由题意得w=(80-50)m+(100-60)(1000-m)=-10m+40000.
∵-10<0,
∴w随m的增大而减小,
∴当m=595时,w取得最大值,最大值为-10×595+40000=34050,此时,1000-m=1000-595=405.答:使农户收益最大,应该安排销售A品种柑橘礼盒595盒,B品种柑橘礼盒405盒,农户在这次农产品展销活动中的最大收益为34050元.