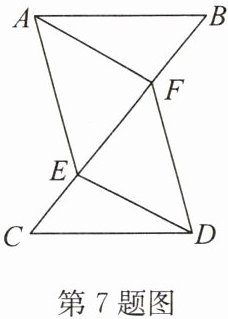
7. 如图,已知 $ AB = CD $,$ AE = DF $,$ CE = BF $,则下列结论:①$ \triangle ABE \cong \triangle DCF $;②$ \angle B = \angle C $;③$ \angle CDF = \angle BAE $;④$ \angle BEA = \angle CFD $;⑤$ CF = BE $. 其中正确的个数是(
A.$ 2 $
B.$ 3 $
C.$ 4 $
D.$ 5 $
D
)
A.$ 2 $
B.$ 3 $
C.$ 4 $
D.$ 5 $
答案:D
解析:
证明:
∵ $ AE = DF $,$ CE = BF $,
∴ $ AE + CE = DF + BF $,即 $ AC = DB $。
在$ \triangle ABE $和$ \triangle DCF $中,
$ AB = CD $,$ AE = DF $,$ BE = CF $(由$ CE = BF $及$ AC = DB $可推得),
∴ $ \triangle ABE \cong \triangle DCF $(SSS),故①正确。
由全等三角形性质得:
$ \angle B = \angle C $,②正确;
$ \angle CDF = \angle BAE $,③正确;
$ \angle BEA = \angle CFD $,④正确;
$ CF = BE $,⑤正确。
综上,①②③④⑤均正确,共5个。
答案:D
∵ $ AE = DF $,$ CE = BF $,
∴ $ AE + CE = DF + BF $,即 $ AC = DB $。
在$ \triangle ABE $和$ \triangle DCF $中,
$ AB = CD $,$ AE = DF $,$ BE = CF $(由$ CE = BF $及$ AC = DB $可推得),
∴ $ \triangle ABE \cong \triangle DCF $(SSS),故①正确。
由全等三角形性质得:
$ \angle B = \angle C $,②正确;
$ \angle CDF = \angle BAE $,③正确;
$ \angle BEA = \angle CFD $,④正确;
$ CF = BE $,⑤正确。
综上,①②③④⑤均正确,共5个。
答案:D
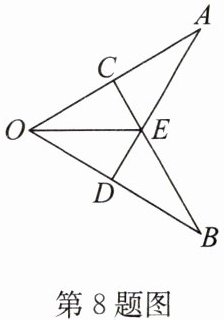
8. 如图,已知 $ OA = OB $,点 $ C $ 在 $ OA $ 上,点 $ D $ 在 $ OB $ 上,$ OC = OD $,$ AD $ 与 $ BC $ 相交于点 $ E $,连接 $ OE $,那么图中全等的三角形共有
4
对.
答案:4
解析:
证明:
1. 在$\triangle OAD$和$\triangle OBC$中,
$\left\{\begin{array}{l} OA=OB\\ \angle AOD=\angle BOC\\ OD=OC\end{array}\right.$,
$\therefore \triangle OAD≌\triangle OBC(SAS)$;
2. $\because \triangle OAD≌\triangle OBC$,
$\therefore \angle A=\angle B$,
$\because OA=OB$,$OC=OD$,
$\therefore AC=BD$,
在$\triangle ACE$和$\triangle BDE$中,
$\left\{\begin{array}{l} \angle A=\angle B\\ \angle AEC=\angle BED\\ AC=BD\end{array}\right.$,
$\therefore \triangle ACE≌\triangle BDE(AAS)$;
3. $\because \triangle ACE≌\triangle BDE$,
$\therefore CE=DE$,
在$\triangle OCE$和$\triangle ODE$中,
$\left\{\begin{array}{l} OC=OD\\ OE=OE\\ CE=DE\end{array}\right.$,
$\therefore \triangle OCE≌\triangle ODE(SSS)$;
4. $\because \triangle OCE≌\triangle ODE$,
$\therefore \angle COE=\angle DOE$,
在$\triangle OAE$和$\triangle OBE$中,
$\left\{\begin{array}{l} OA=OB\\ \angle AOE=\angle BOE\\ OE=OE\end{array}\right.$,
$\therefore \triangle OAE≌\triangle OBE(SAS)$。
图中全等的三角形共有4对。
4
1. 在$\triangle OAD$和$\triangle OBC$中,
$\left\{\begin{array}{l} OA=OB\\ \angle AOD=\angle BOC\\ OD=OC\end{array}\right.$,
$\therefore \triangle OAD≌\triangle OBC(SAS)$;
2. $\because \triangle OAD≌\triangle OBC$,
$\therefore \angle A=\angle B$,
$\because OA=OB$,$OC=OD$,
$\therefore AC=BD$,
在$\triangle ACE$和$\triangle BDE$中,
$\left\{\begin{array}{l} \angle A=\angle B\\ \angle AEC=\angle BED\\ AC=BD\end{array}\right.$,
$\therefore \triangle ACE≌\triangle BDE(AAS)$;
3. $\because \triangle ACE≌\triangle BDE$,
$\therefore CE=DE$,
在$\triangle OCE$和$\triangle ODE$中,
$\left\{\begin{array}{l} OC=OD\\ OE=OE\\ CE=DE\end{array}\right.$,
$\therefore \triangle OCE≌\triangle ODE(SSS)$;
4. $\because \triangle OCE≌\triangle ODE$,
$\therefore \angle COE=\angle DOE$,
在$\triangle OAE$和$\triangle OBE$中,
$\left\{\begin{array}{l} OA=OB\\ \angle AOE=\angle BOE\\ OE=OE\end{array}\right.$,
$\therefore \triangle OAE≌\triangle OBE(SAS)$。
图中全等的三角形共有4对。
4
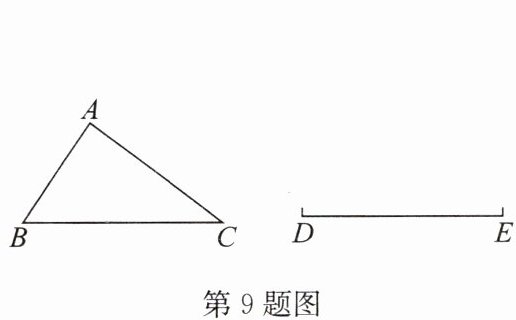
9. 如图,已知 $ \triangle ABC (AC > AB) $,$ DE = BC $,以 $ D $,$ E $ 为顶点作三角形,使所作的三角形与 $ \triangle ABC $ 全等,这样的三角形最多可以作出
4
个.
答案:4
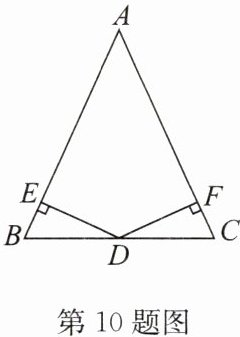
10. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ D $ 是 $ BC $ 边的中点,$ DE \perp AB $,$ DF \perp AC $,垂足分别是 $ E $,$ F $. 求证:$ AE = AF $.

答案:证明:连接AD.
∵D是BC边的中点,
∴BD=CD.
在△ABD和△ACD中,$\left\{\begin{array}{l} AB=AC,\\ AD=AD,\\ BD=CD,\end{array}\right. $
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD.
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
在△AED和△AFD中,$\left\{\begin{array}{l} ∠EAD=∠FAD,\\ ∠AED=∠AFD,\\ AD=AD,\end{array}\right. $
∴△AED≌△AFD(AAS),
∴AE=AF.
∵D是BC边的中点,
∴BD=CD.
在△ABD和△ACD中,$\left\{\begin{array}{l} AB=AC,\\ AD=AD,\\ BD=CD,\end{array}\right. $
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD.
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
在△AED和△AFD中,$\left\{\begin{array}{l} ∠EAD=∠FAD,\\ ∠AED=∠AFD,\\ AD=AD,\end{array}\right. $
∴△AED≌△AFD(AAS),
∴AE=AF.
11. 我们对课本里特殊四边形的学习,一般先学习图形的定义,再探索发现其性质和判定方法,然后通过解决简单的问题巩固所学知识,请解决以下问题:
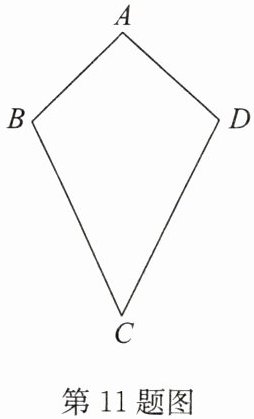
如图,我们把满足 $ AB = AD $、$ CB = CD $ 且 $ AB \neq BC $ 的四边形 $ ABCD $ 叫作筝形.
(1)写出筝形的两个性质(定义除外);
(2)写出筝形的两个判定方法(定义除外),并选出一个进行证明.
如图,我们把满足 $ AB = AD $、$ CB = CD $ 且 $ AB \neq BC $ 的四边形 $ ABCD $ 叫作筝形.
(1)写出筝形的两个性质(定义除外);
(2)写出筝形的两个判定方法(定义除外),并选出一个进行证明.

答案:
解:
(1)性质1:只有一组对角相等;
性质2:只有一条对角线平分对角.(答案不唯一)
(2)判定方法1:只有一条对角线平分对角的四边形是筝形;
判定方法2:两条对角线互相垂直且只有一条被平分的四边形是筝形.
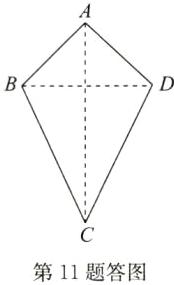
证明方法1:连接AC,BD,如答图.
在△ABC和△ADC中,$\left\{\begin{array}{l} ∠BAC=∠DAC,\\ AC=AC,\\ ∠BCA=∠DCA,\end{array}\right. $
∴△ABC≌△ADC,
∴AB=AD,CB=CD,①
易知AC⊥BD,
又
∵∠ABD≠∠CBD,
∴∠BAC≠∠BCA,AB≠BC,②
由①②知四边形ABCD是筝形.
解:
(1)性质1:只有一组对角相等;
性质2:只有一条对角线平分对角.(答案不唯一)
(2)判定方法1:只有一条对角线平分对角的四边形是筝形;
判定方法2:两条对角线互相垂直且只有一条被平分的四边形是筝形.
证明方法1:连接AC,BD,如答图.
在△ABC和△ADC中,$\left\{\begin{array}{l} ∠BAC=∠DAC,\\ AC=AC,\\ ∠BCA=∠DCA,\end{array}\right. $
∴△ABC≌△ADC,
∴AB=AD,CB=CD,①
易知AC⊥BD,
又
∵∠ABD≠∠CBD,
∴∠BAC≠∠BCA,AB≠BC,②
由①②知四边形ABCD是筝形.
