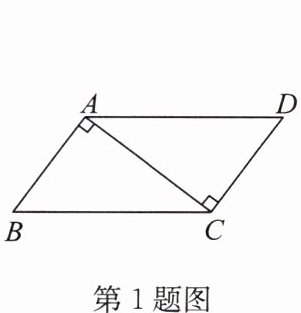
1. (2024·南京鼓楼区期中)如图,已知 $ AB \perp AC $,$ CD \perp AC $,若用“$ HL $”判定 $ \triangle ABC $ 与 $ \triangle CDA $ 全等,则需要添加的条件是(
A.$ \angle B = \angle D $
B.$ \angle ACB = \angle CAD $
C.$ AB = CD $
D.$ AD = CB $
D
)
A.$ \angle B = \angle D $
B.$ \angle ACB = \angle CAD $
C.$ AB = CD $
D.$ AD = CB $
答案:D
解析:
证明:
∵ $ AB \perp AC $,$ CD \perp AC $,
∴ $ \angle BAC = \angle DCA = 90° $,即 $ \triangle ABC $ 和 $ \triangle CDA $ 均为直角三角形,且公共边 $ AC $ 为直角边。
要使用“$ HL $”判定全等,需添加斜边相等的条件。
在 $ \triangle ABC $ 中,斜边为 $ BC $;在 $ \triangle CDA $ 中,斜边为 $ AD $。
∴ 需添加条件 $ AD = CB $。
D
∵ $ AB \perp AC $,$ CD \perp AC $,
∴ $ \angle BAC = \angle DCA = 90° $,即 $ \triangle ABC $ 和 $ \triangle CDA $ 均为直角三角形,且公共边 $ AC $ 为直角边。
要使用“$ HL $”判定全等,需添加斜边相等的条件。
在 $ \triangle ABC $ 中,斜边为 $ BC $;在 $ \triangle CDA $ 中,斜边为 $ AD $。
∴ 需添加条件 $ AD = CB $。
D
2. (2024·钟吾初中期中)下列条件不能判定两个直角三角形全等的是(
A.一条直角边及其对角对应相等
B.斜边和一条直角边对应相等
C.斜边和一锐角对应相等
D.两个锐角对应相等
D
)A.一条直角边及其对角对应相等
B.斜边和一条直角边对应相等
C.斜边和一锐角对应相等
D.两个锐角对应相等
答案:D
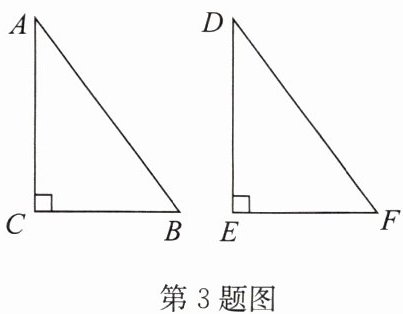
3. 如图,在 $ Rt \triangle ABC $ 和 $ Rt \triangle DFE $ 中,$ \angle C = \angle E = 90^{\circ} $,$ AC = DE $. 若根据判定定理“$ HL $”得到 $ Rt \triangle ABC \cong Rt \triangle DFE $,则需要补充的条件是
AB=DF
.
答案:AB=DF
4. (2024·宿豫期中)如图,$ AC \perp BC $,$ AD \perp BD $,要使 $ \triangle ABC \cong \triangle ABD $,还需要添加的一个条件是
AC=AD
.(只要写出一种情况即可)
答案:答案不唯一,如AC=AD
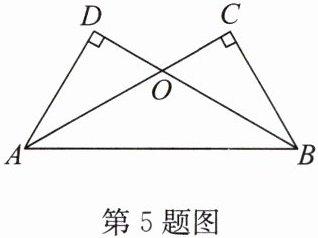
5. 如图,已知 $ AC \perp BC $,$ BD \perp AD $,$ AC $ 与 $ BD $ 交于点 $ O $,$ AC = BD $.
求证:(1)$ BC = AD $;(2)$ \triangle OAB $ 是等腰三角形.
求证:(1)$ BC = AD $;(2)$ \triangle OAB $ 是等腰三角形.

答案:证明:
(1)
∵AC⊥BC,BD⊥AD,
∴∠C=∠D=90°.
又
∵AC=BD,AB=BA,
∴Rt△ABD≌Rt△BAC(HL).
∴BC=AD.
(2)
∵∠D=∠C,∠AOD=∠BOC,AD=BC,
∴△AOD≌△BOC(AAS).
∴OA=OB.
∴△OAB是等腰三角形.
(1)
∵AC⊥BC,BD⊥AD,
∴∠C=∠D=90°.
又
∵AC=BD,AB=BA,
∴Rt△ABD≌Rt△BAC(HL).
∴BC=AD.
(2)
∵∠D=∠C,∠AOD=∠BOC,AD=BC,
∴△AOD≌△BOC(AAS).
∴OA=OB.
∴△OAB是等腰三角形.
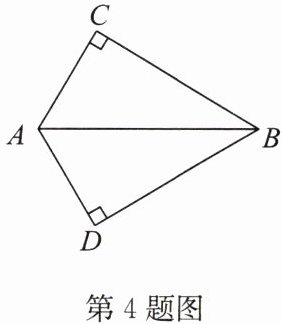
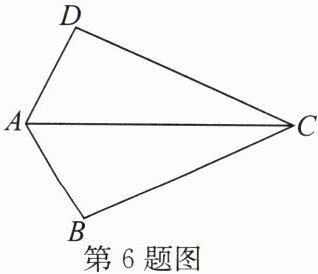
6. 如图,$ AB = AD $,添加下列一个条件后,仍无法判定 $ \triangle ABC \cong \triangle ADC $ 的是(
A.$ \angle BAC = \angle DAC $
B.$ \angle BCA = \angle DCA $
C.$ CB = CD $
D.$ \angle B = \angle D = 90^{\circ} $
B
)
A.$ \angle BAC = \angle DAC $
B.$ \angle BCA = \angle DCA $
C.$ CB = CD $
D.$ \angle B = \angle D = 90^{\circ} $
答案:B
解析:
要判定$\triangle ABC \cong \triangle ADC$,已知$AB = AD$,公共边$AC = AC$。
选项A:若$\angle BAC = \angle DAC$,根据“边角边”(SAS)定理,$\triangle ABC \cong \triangle ADC$。
选项B:若$\angle BCA = \angle DCA$,此时为“边边角”(SSA),无法判定$\triangle ABC \cong \triangle ADC$。
选项C:若$CB = CD$,根据“边边边”(SSS)定理,$\triangle ABC \cong \triangle ADC$。
选项D:若$\angle B = \angle D = 90°$,根据“斜边直角边”(HL)定理,$\triangle ABC \cong \triangle ADC$。
答案:B
选项A:若$\angle BAC = \angle DAC$,根据“边角边”(SAS)定理,$\triangle ABC \cong \triangle ADC$。
选项B:若$\angle BCA = \angle DCA$,此时为“边边角”(SSA),无法判定$\triangle ABC \cong \triangle ADC$。
选项C:若$CB = CD$,根据“边边边”(SSS)定理,$\triangle ABC \cong \triangle ADC$。
选项D:若$\angle B = \angle D = 90°$,根据“斜边直角边”(HL)定理,$\triangle ABC \cong \triangle ADC$。
答案:B