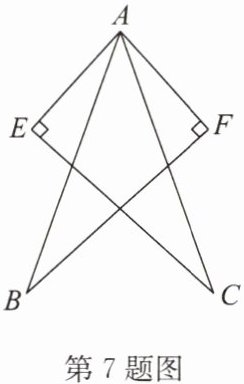
7. (2025·张家港期末)如图,已知 $ AB = AC $,$ AE = AF $,$ AF \perp BF $,$ AE \perp EC $,则图中全等的三角形共有(
A.4 对
B.3 对
C.2 对
D.1 对
A
)
A.4 对
B.3 对
C.2 对
D.1 对
答案:A
解析:
证明:
1. 在$Rt\triangle AEC$和$Rt\triangle AFB$中,
$\because AE=AF$,$AC=AB$,
$\therefore Rt\triangle AEC \cong Rt\triangle AFB$(HL),得$BF=CE$,$\angle B=\angle C$。
2. 在$\triangle ABE$和$\triangle ACF$中,
$\because AB=AC$,$\angle BAE=\angle CAF$(公共角),$AE=AF$,
$\therefore \triangle ABE \cong \triangle ACF$(SAS),得$BE=CF$。
3. 在$\triangle BDE$和$\triangle CDF$中(设$BF$与$CE$交于点$D$),
$\because \angle B=\angle C$,$\angle BDE=\angle CDF$(对顶角),$BE=CF$,
$\therefore \triangle BDE \cong \triangle CDF$(AAS)。
4. 在$\triangle ABD$和$\triangle ACD$中,
$\because AB=AC$,$\angle B=\angle C$,$BD=CD$(由$\triangle BDE \cong \triangle CDF$得),
$\therefore \triangle ABD \cong \triangle ACD$(SAS)。
综上,全等三角形共4对。
答案:A
1. 在$Rt\triangle AEC$和$Rt\triangle AFB$中,
$\because AE=AF$,$AC=AB$,
$\therefore Rt\triangle AEC \cong Rt\triangle AFB$(HL),得$BF=CE$,$\angle B=\angle C$。
2. 在$\triangle ABE$和$\triangle ACF$中,
$\because AB=AC$,$\angle BAE=\angle CAF$(公共角),$AE=AF$,
$\therefore \triangle ABE \cong \triangle ACF$(SAS),得$BE=CF$。
3. 在$\triangle BDE$和$\triangle CDF$中(设$BF$与$CE$交于点$D$),
$\because \angle B=\angle C$,$\angle BDE=\angle CDF$(对顶角),$BE=CF$,
$\therefore \triangle BDE \cong \triangle CDF$(AAS)。
4. 在$\triangle ABD$和$\triangle ACD$中,
$\because AB=AC$,$\angle B=\angle C$,$BD=CD$(由$\triangle BDE \cong \triangle CDF$得),
$\therefore \triangle ABD \cong \triangle ACD$(SAS)。
综上,全等三角形共4对。
答案:A
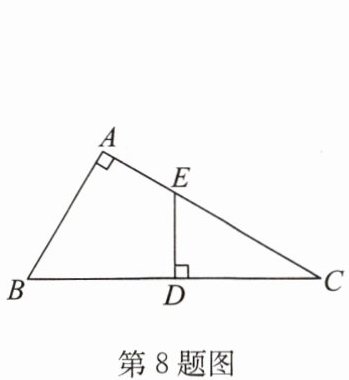
8. 如图,$ D $ 为 $ Rt \triangle ABC $ 斜边 $ BC $ 的中点,过点 $ D $ 作 $ BC $ 的垂线,交 $ AC $ 于点 $ E $,且 $ AE = DE $,若 $ BC = 12 $,则 $ AB = $
6
.
答案:6
解析:
解:连接 $ BE $。
因为 $ D $ 为 $ Rt\triangle ABC $ 斜边 $ BC $ 的中点,$ BC = 12 $,所以 $ BD = DC = 6 $。
因为 $ ED \perp BC $,所以 $ \angle EDB = \angle EDC = 90° $。
在 $ Rt\triangle EDB $ 和 $ Rt\triangle EDC $ 中,$ ED = ED $,$ BD = DC $,所以 $ Rt\triangle EDB \cong Rt\triangle EDC $(HL),故 $ EB = EC $。
设 $ AB = x $,$ AE = DE = y $,则 $ EC = EB = AC - AE $。
在 $ Rt\triangle ABE $ 中,$ AB^2 + AE^2 = BE^2 $,即 $ x^2 + y^2 = BE^2 $。
在 $ Rt\triangle ABC $ 中,$ AB^2 + AC^2 = BC^2 $,设 $ AC = z $,则 $ x^2 + z^2 = 144 $,且 $ z = AE + EC = y + BE $,又因为 $ BE = z - y $,所以 $ x^2 + y^2 = (z - y)^2 $,展开得 $ x^2 + y^2 = z^2 - 2yz + y^2 $,即 $ x^2 = z^2 - 2yz $。
由 $ x^2 + z^2 = 144 $ 得 $ z^2 = 144 - x^2 $,代入上式得 $ x^2 = 144 - x^2 - 2yz $,即 $ 2x^2 + 2yz = 144 $,$ x^2 + yz = 72 $。
在 $ Rt\triangle EDC $ 中,$ DE^2 + DC^2 = EC^2 $,即 $ y^2 + 6^2 = (z - y)^2 $,展开得 $ y^2 + 36 = z^2 - 2yz + y^2 $,即 $ z^2 - 2yz = 36 $。
因为 $ z^2 = 144 - x^2 $,所以 $ 144 - x^2 - 2yz = 36 $,即 $ x^2 + 2yz = 108 $。
联立 $ x^2 + yz = 72 $ 和 $ x^2 + 2yz = 108 $,两式相减得 $ yz = 36 $,代入 $ x^2 + 36 = 72 $,得 $ x^2 = 36 $,故 $ x = 6 $($ x > 0 $)。
$ 6 $
因为 $ D $ 为 $ Rt\triangle ABC $ 斜边 $ BC $ 的中点,$ BC = 12 $,所以 $ BD = DC = 6 $。
因为 $ ED \perp BC $,所以 $ \angle EDB = \angle EDC = 90° $。
在 $ Rt\triangle EDB $ 和 $ Rt\triangle EDC $ 中,$ ED = ED $,$ BD = DC $,所以 $ Rt\triangle EDB \cong Rt\triangle EDC $(HL),故 $ EB = EC $。
设 $ AB = x $,$ AE = DE = y $,则 $ EC = EB = AC - AE $。
在 $ Rt\triangle ABE $ 中,$ AB^2 + AE^2 = BE^2 $,即 $ x^2 + y^2 = BE^2 $。
在 $ Rt\triangle ABC $ 中,$ AB^2 + AC^2 = BC^2 $,设 $ AC = z $,则 $ x^2 + z^2 = 144 $,且 $ z = AE + EC = y + BE $,又因为 $ BE = z - y $,所以 $ x^2 + y^2 = (z - y)^2 $,展开得 $ x^2 + y^2 = z^2 - 2yz + y^2 $,即 $ x^2 = z^2 - 2yz $。
由 $ x^2 + z^2 = 144 $ 得 $ z^2 = 144 - x^2 $,代入上式得 $ x^2 = 144 - x^2 - 2yz $,即 $ 2x^2 + 2yz = 144 $,$ x^2 + yz = 72 $。
在 $ Rt\triangle EDC $ 中,$ DE^2 + DC^2 = EC^2 $,即 $ y^2 + 6^2 = (z - y)^2 $,展开得 $ y^2 + 36 = z^2 - 2yz + y^2 $,即 $ z^2 - 2yz = 36 $。
因为 $ z^2 = 144 - x^2 $,所以 $ 144 - x^2 - 2yz = 36 $,即 $ x^2 + 2yz = 108 $。
联立 $ x^2 + yz = 72 $ 和 $ x^2 + 2yz = 108 $,两式相减得 $ yz = 36 $,代入 $ x^2 + 36 = 72 $,得 $ x^2 = 36 $,故 $ x = 6 $($ x > 0 $)。
$ 6 $
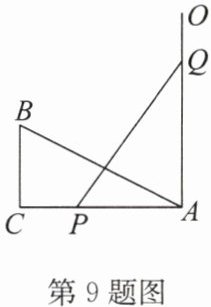
9. 如图,在 $ Rt \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ AC = 10 $,$ BC = 5 $,线段 $ PQ = AB $,点 $ P $,$ Q $ 分别在边 $ AC $ 和过点 $ A $ 且垂直于 $ AC $ 的射线 $ AO $ 上运动,当 $ AP = $
5或10
时,$ \triangle ABC $ 和 $ \triangle PQA $ 全等.
答案:5或10
解析:
解:
$\because \angle C=90^{\circ}$,$AO \perp AC$,
$\therefore \angle C=\angle PAQ=90^{\circ}$。
情况1:当$AP=BC=5$时
在$Rt\triangle ABC$和$Rt\triangle QPA$中,
$\left\{\begin{array}{l} AP=BC=5 \\ PQ=AB \end{array}\right.$,
$\therefore Rt\triangle ABC \cong Rt\triangle QPA(HL)$。
情况2:当$AP=AC=10$时
在$Rt\triangle ABC$和$Rt\triangle PQA$中,
$\left\{\begin{array}{l} AP=AC=10 \\ PQ=AB \end{array}\right.$,
$\therefore Rt\triangle ABC \cong Rt\triangle PQA(HL)$。
综上,$AP=5$或$10$。
5或10
$\because \angle C=90^{\circ}$,$AO \perp AC$,
$\therefore \angle C=\angle PAQ=90^{\circ}$。
情况1:当$AP=BC=5$时
在$Rt\triangle ABC$和$Rt\triangle QPA$中,
$\left\{\begin{array}{l} AP=BC=5 \\ PQ=AB \end{array}\right.$,
$\therefore Rt\triangle ABC \cong Rt\triangle QPA(HL)$。
情况2:当$AP=AC=10$时
在$Rt\triangle ABC$和$Rt\triangle PQA$中,
$\left\{\begin{array}{l} AP=AC=10 \\ PQ=AB \end{array}\right.$,
$\therefore Rt\triangle ABC \cong Rt\triangle PQA(HL)$。
综上,$AP=5$或$10$。
5或10
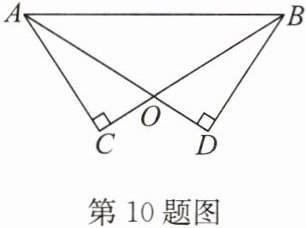
10. 如图,$ AD $ 与 $ BC $ 相交于点 $ O $,$ AD = BC $,$ \angle C = \angle D = 90^{\circ} $.
(1)求证:$ \triangle ABC \cong \triangle BAD $;
(2)若 $ \angle ABC = 35^{\circ} $,求 $ \angle CAO $ 的度数.
(1)求证:$ \triangle ABC \cong \triangle BAD $;
(2)若 $ \angle ABC = 35^{\circ} $,求 $ \angle CAO $ 的度数.

答案:
(1)证明:
∵∠C=∠D=90°,
∴△ABC和△BAD都是直角三角形.
在Rt△ABC和Rt△BAD中,{AB=BA,
BC=AD,
∴Rt△ABC≌Rt△BAD(HL).
(2)解:
∵Rt△ABC≌Rt△BAD,
∴∠ABC=∠BAD=35°.
∵∠C=90°,
∴∠BAC=90°-35°=55°,
∴∠CAO=∠CAB-∠BAD=20°.
(1)证明:
∵∠C=∠D=90°,
∴△ABC和△BAD都是直角三角形.
在Rt△ABC和Rt△BAD中,{AB=BA,
BC=AD,
∴Rt△ABC≌Rt△BAD(HL).
(2)解:
∵Rt△ABC≌Rt△BAD,
∴∠ABC=∠BAD=35°.
∵∠C=90°,
∴∠BAC=90°-35°=55°,
∴∠CAO=∠CAB-∠BAD=20°.
11. (2025·鼓楼区期末)如图,已知 $ DE \perp AC $ 于点 $ E $,$ BF \perp AC $ 于点 $ F $,$ AD = BC $,$ DE = BF $. 试探究 $ AB $ 与 $ CD $ 的数量关系与位置关系,并说明理由.
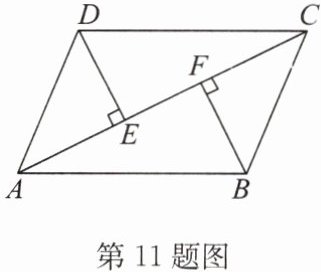

答案:解:AB=CD且AB//CD.理由:
∵DE⊥AC于点E,BF⊥AC于点F,
∴∠AED=∠BFC=∠DEC=∠BFA=90°.
在Rt△AED和Rt△CFB中,{AD=CB,
DE=BF,
∴Rt△AED≌Rt△CFB(HL).
∴AE=CF.
∴AE+EF=CF+EF,即AF=CE.
又
∵∠DEC=∠BFA=90°,DE=BF,
∴△AFB≌△CED(SAS).
∴AB=CD,∠BAF=∠DCE.
∴AB//CD.
综上,AB=CD且AB//CD.
∵DE⊥AC于点E,BF⊥AC于点F,
∴∠AED=∠BFC=∠DEC=∠BFA=90°.
在Rt△AED和Rt△CFB中,{AD=CB,
DE=BF,
∴Rt△AED≌Rt△CFB(HL).
∴AE=CF.
∴AE+EF=CF+EF,即AF=CE.
又
∵∠DEC=∠BFA=90°,DE=BF,
∴△AFB≌△CED(SAS).
∴AB=CD,∠BAF=∠DCE.
∴AB//CD.
综上,AB=CD且AB//CD.
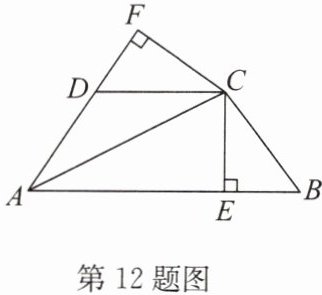
12. 如图,已知 $ AC $ 平分 $ \angle BAF $,$ CE \perp AB $ 于点 $ E $,$ CF \perp AF $ 于点 $ F $,且 $ BC = DC $.
(1)求证:$ BE = DF $;
(2)若 $ AB = 21 $,$ AD = 9 $,求 $ DF $ 的长.
(1)求证:$ BE = DF $;
(2)若 $ AB = 21 $,$ AD = 9 $,求 $ DF $ 的长.

答案:
(1)证明:
∵AC平分∠BAF,
∴∠CAE=∠CAF.
∵CE⊥AB,CF⊥AF,
∴∠CEA=∠CEB=∠F=90°.
又
∵AC=AC,
∴△ACE≌△ACF(AAS).
∴CE=CF.
又
∵BC=DC,
∴Rt△CDF≌Rt△CBE(HL).
∴BE=DF.
(2)解:由
(1)知△ACE≌△ACF,
∴AE=AF.
又由
(1)知BE=DF,
∴AD+DF=AB-DF.
∵AB=21,AD=9,
∴9+DF=21-DF.
∴DF=6.
(1)证明:
∵AC平分∠BAF,
∴∠CAE=∠CAF.
∵CE⊥AB,CF⊥AF,
∴∠CEA=∠CEB=∠F=90°.
又
∵AC=AC,
∴△ACE≌△ACF(AAS).
∴CE=CF.
又
∵BC=DC,
∴Rt△CDF≌Rt△CBE(HL).
∴BE=DF.
(2)解:由
(1)知△ACE≌△ACF,
∴AE=AF.
又由
(1)知BE=DF,
∴AD+DF=AB-DF.
∵AB=21,AD=9,
∴9+DF=21-DF.
∴DF=6.