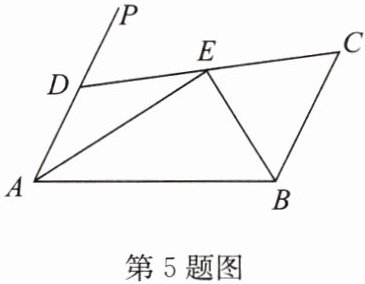
5. 如图,已知 $AD// BC,\angle PAB$ 的平分线与 $\angle CBA$ 的平分线相交于点 $E$,连接 $CE$ 并延长交 $AP$ 于点 $D$. 求证:$AD+BC= AB$.

答案:
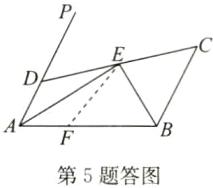
证明:如答图,在AB上截取AF=AD,连接EF.
∵AE平分∠PAB,
∴∠DAE=∠FAE;
在△DAE和△FAE中,$\left\{\begin{array}{l} AD=AF,\\ ∠DAE=∠FAE,\\ AE=AE,\end{array}\right. $
∴△DAE≌△FAE(SAS),
∴∠ADE=∠AFE.
∵AD//BC,
∴∠ADE+∠C=180°.
∵∠AFE+∠EFB=180°,
∴∠EFB=∠C.
∵BE平分∠ABC,
∴∠EBF=∠EBC.
在△BEF和△BEC中,$\left\{\begin{array}{l} ∠EFB=∠C,\\ ∠EBF=∠EBC,\\ BE=BE,\end{array}\right. $
∴△BEF≌△BEC(AAS),
∴BF=BC.
又
∵AD=AF,
∴AD+BC=AF+BF=AB.
证明:如答图,在AB上截取AF=AD,连接EF.
∵AE平分∠PAB,
∴∠DAE=∠FAE;

在△DAE和△FAE中,$\left\{\begin{array}{l} AD=AF,\\ ∠DAE=∠FAE,\\ AE=AE,\end{array}\right. $
∴△DAE≌△FAE(SAS),
∴∠ADE=∠AFE.
∵AD//BC,
∴∠ADE+∠C=180°.
∵∠AFE+∠EFB=180°,
∴∠EFB=∠C.
∵BE平分∠ABC,
∴∠EBF=∠EBC.
在△BEF和△BEC中,$\left\{\begin{array}{l} ∠EFB=∠C,\\ ∠EBF=∠EBC,\\ BE=BE,\end{array}\right. $
∴△BEF≌△BEC(AAS),
∴BF=BC.
又
∵AD=AF,
∴AD+BC=AF+BF=AB.
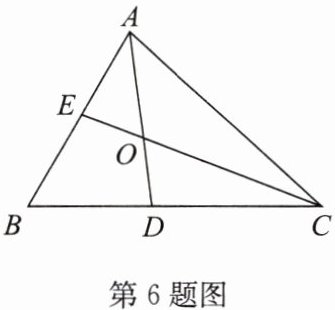
6. 如图,在 $\triangle ABC$ 中,$AD,CE$ 分别平分 $\angle BAC,\angle ACB$,且 $AD,CE$ 交于点 $O$,若 $\angle ABC= 60^{\circ}$.
(1)求 $\angle AOC$ 的度数;(2)求证:$AC= AE+CD$.
(1)求 $\angle AOC$ 的度数;(2)求证:$AC= AE+CD$.

答案:
(1)解:
∵AD,CE分别平分∠BAC,∠ACB,
∴∠ECA+∠DAC=$\frac{1}{2}$∠ACB+$\frac{1}{2}$∠BAC=$\frac{1}{2}$(∠ACB+∠BAC)=$\frac{1}{2}$(180°−∠B)=60°,
∴∠AOC=180°−∠ECA−∠DAC=120°.
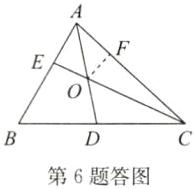
(2)证明:如答图,在AC上截取AF=AE,连接OF;
∵AD平分∠BAC,
∴∠EAO=∠FAO.
在△AEO和△AFO中,$\left\{\begin{array}{l} AE=AF,\\ ∠EAO=∠FAO,\\ AO=AO,\end{array}\right. $
∴△AEO≌△AFO(SAS),
∴∠AOE=∠AOF;
由
(1)知∠AOC=120°,
∴∠AOE=∠AOF=∠COD=180°−120°=60°,
∴∠COF=180°−60°−60°=60°.
∵CE平分∠ACB,
∴∠FCO=∠DCO.
在△FOC和△DOC中,$\left\{\begin{array}{l} ∠COF=∠COD,\\ CO=CO,\\ ∠FCO=∠DCO,\end{array}\right. $
∴△FOC≌△DOC(ASA),
∴DC=FC;
∵AC=AF+FC,
∴AC=AE+CD.
(1)解:
∵AD,CE分别平分∠BAC,∠ACB,
∴∠ECA+∠DAC=$\frac{1}{2}$∠ACB+$\frac{1}{2}$∠BAC=$\frac{1}{2}$(∠ACB+∠BAC)=$\frac{1}{2}$(180°−∠B)=60°,
∴∠AOC=180°−∠ECA−∠DAC=120°.
(2)证明:如答图,在AC上截取AF=AE,连接OF;

∵AD平分∠BAC,
∴∠EAO=∠FAO.
在△AEO和△AFO中,$\left\{\begin{array}{l} AE=AF,\\ ∠EAO=∠FAO,\\ AO=AO,\end{array}\right. $
∴△AEO≌△AFO(SAS),
∴∠AOE=∠AOF;
由
(1)知∠AOC=120°,
∴∠AOE=∠AOF=∠COD=180°−120°=60°,
∴∠COF=180°−60°−60°=60°.
∵CE平分∠ACB,
∴∠FCO=∠DCO.
在△FOC和△DOC中,$\left\{\begin{array}{l} ∠COF=∠COD,\\ CO=CO,\\ ∠FCO=∠DCO,\end{array}\right. $
∴△FOC≌△DOC(ASA),
∴DC=FC;
∵AC=AF+FC,
∴AC=AE+CD.
7. 如图,已知 $\angle B= \angle C= 90^{\circ},EB= EC,DE$ 平分 $\angle ADC$,求证:$AE$ 是 $\angle DAB$ 的平分线.
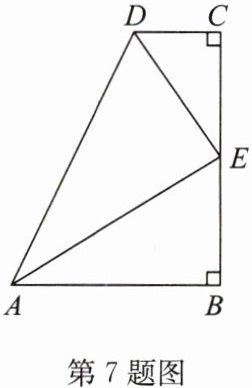

答案:证明:过点E作EF⊥AD于点F.
∵DE平分∠ADC,
∴∠CDE=∠FDE.
∵∠C=90°,EF⊥AD,
∴∠C=∠DFE.
在△CDE与△FDE中,$\left\{\begin{array}{l} ∠CDE=∠FDE,\\ ∠C=∠DFE,\\ DE=DE,\end{array}\right. $
∴△CDE≌△FDE(AAS),
∴EC=EF.
∵EB=EC,
∴EF=BE.
在Rt△AFE与Rt△ABE中,$\left\{\begin{array}{l} AE=AE,\\ EF=EB,\end{array}\right. $
∴Rt△AFE≌Rt△ABE(HL),
∴∠FAE=∠BAE,
∴AE是∠DAB的平分线.
∵DE平分∠ADC,
∴∠CDE=∠FDE.
∵∠C=90°,EF⊥AD,
∴∠C=∠DFE.
在△CDE与△FDE中,$\left\{\begin{array}{l} ∠CDE=∠FDE,\\ ∠C=∠DFE,\\ DE=DE,\end{array}\right. $
∴△CDE≌△FDE(AAS),
∴EC=EF.
∵EB=EC,
∴EF=BE.
在Rt△AFE与Rt△ABE中,$\left\{\begin{array}{l} AE=AE,\\ EF=EB,\end{array}\right. $
∴Rt△AFE≌Rt△ABE(HL),
∴∠FAE=∠BAE,
∴AE是∠DAB的平分线.
8. 如图,$AO\perp OM,OA= 7,B$ 为射线 $OM$ 上的一个动点,分别以 $OB,AB$ 为直角边,$B$ 为直角顶点,在 $OM$ 两侧作等腰直角三角形 $OBF$、等腰直角三角形 $ABE$,连接 $EF$ 交 $OM$ 于点 $P$,当点 $B$ 在射线 $OM$ 上移动时,求 $PB$ 的长.
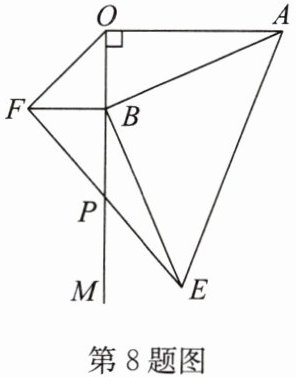

答案:
解:如答图,过点E作EN⊥BM,垂足为N.
∵∠AOB=∠ABE=∠BNE=90°,
∴∠ABO+∠BAO=∠ABO+∠NBE=90°,
∴∠BAO=∠NBE.
∵△OBF,△ABE均为等腰直角三角形,
∴AB=BE,BF=OB.
在△AOB和△BNE中,$\left\{\begin{array}{l} ∠BAO=∠EBN,\\ ∠AOB=∠BNE,\\ AB=BE,\end{array}\right. $
∴△AOB≌△BNE(AAS).
∴BO=NE,BN=AO.
∵BF=OB,
∴BF=NE.
在△BPF和△NPE中,$\left\{\begin{array}{l} ∠FBP=∠ENP,\\ ∠FPB=∠EPN,\\ BF=NE,\end{array}\right. $
∴△BPF≌△NPE(AAS).
∴BP=NP=$\frac{1}{2}$BN.
∵BN=AO,
∴BP=$\frac{1}{2}$AO=$\frac{1}{2}$×7=$\frac{7}{2}$.
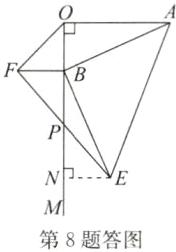
解:如答图,过点E作EN⊥BM,垂足为N.
∵∠AOB=∠ABE=∠BNE=90°,
∴∠ABO+∠BAO=∠ABO+∠NBE=90°,
∴∠BAO=∠NBE.
∵△OBF,△ABE均为等腰直角三角形,
∴AB=BE,BF=OB.
在△AOB和△BNE中,$\left\{\begin{array}{l} ∠BAO=∠EBN,\\ ∠AOB=∠BNE,\\ AB=BE,\end{array}\right. $
∴△AOB≌△BNE(AAS).
∴BO=NE,BN=AO.
∵BF=OB,
∴BF=NE.
在△BPF和△NPE中,$\left\{\begin{array}{l} ∠FBP=∠ENP,\\ ∠FPB=∠EPN,\\ BF=NE,\end{array}\right. $
∴△BPF≌△NPE(AAS).
∴BP=NP=$\frac{1}{2}$BN.
∵BN=AO,
∴BP=$\frac{1}{2}$AO=$\frac{1}{2}$×7=$\frac{7}{2}$.
