1. 如图,AC 与 BD 相交于点 O,AB = CD,∠A = ∠D,不添加辅助线,判定△ABO ≌ △DCO 的依据是(

A.SSS
B.SAS
C.HL
D.AAS
D
)
A.SSS
B.SAS
C.HL
D.AAS
答案:D
解析:
证明:在△ABO和△DCO中,
∵∠A=∠D,
∠AOB=∠DOC(对顶角相等),
AB=CD,
∴△ABO≌△DCO(AAS)。
D
∵∠A=∠D,
∠AOB=∠DOC(对顶角相等),
AB=CD,
∴△ABO≌△DCO(AAS)。
D
2. 如图,工人师傅设计了一种测量零件内径 AB 的卡钳,卡钳交叉点 O 为 AA',BB'的中点,只要量出 A'B'的长度,就可以知道该零件内径 AB 的长度. 依据的数学基本事实是(

A.两角及其夹边分别相等的两个三角形全等
B.两边及其夹角分别相等的两个三角形全等
C.两点确定一条直线
D.两点之间线段最短
B
)
A.两角及其夹边分别相等的两个三角形全等
B.两边及其夹角分别相等的两个三角形全等
C.两点确定一条直线
D.两点之间线段最短
答案:B
解析:
证明:
∵O为AA',BB'的中点,
∴AO=A'O,BO=B'O。
在△AOB和△A'OB'中,
$\left\{\begin{array}{l} AO=A'O \\ ∠AOB=∠A'OB' \\ BO=B'O\end{array}\right.$
∴△AOB≌△A'OB'(SAS)。
∴AB=A'B'。
依据的数学基本事实是两边及其夹角分别相等的两个三角形全等。
B
∵O为AA',BB'的中点,
∴AO=A'O,BO=B'O。
在△AOB和△A'OB'中,
$\left\{\begin{array}{l} AO=A'O \\ ∠AOB=∠A'OB' \\ BO=B'O\end{array}\right.$
∴△AOB≌△A'OB'(SAS)。
∴AB=A'B'。
依据的数学基本事实是两边及其夹角分别相等的两个三角形全等。
B
3. 如图,∠BAC = ∠DAC,若要使△ABC ≌ △ADC,还需要添加一个条件,则这个条件不能是(

A.BC = DC
B.AB = AD
C.∠B = ∠D
D.∠ACB = ∠ACD
A
)
A.BC = DC
B.AB = AD
C.∠B = ∠D
D.∠ACB = ∠ACD
答案:A
解析:
证明:已知∠BAC=∠DAC,AC为公共边。
若添加条件B(AB=AD),则根据SAS可证△ABC≌△ADC;
若添加条件C(∠B=∠D),则根据AAS可证△ABC≌△ADC;
若添加条件D(∠ACB=∠ACD),则根据ASA可证△ABC≌△ADC;
若添加条件A(BC=DC),为SSA,不能证明△ABC≌△ADC。
A
若添加条件B(AB=AD),则根据SAS可证△ABC≌△ADC;
若添加条件C(∠B=∠D),则根据AAS可证△ABC≌△ADC;
若添加条件D(∠ACB=∠ACD),则根据ASA可证△ABC≌△ADC;
若添加条件A(BC=DC),为SSA,不能证明△ABC≌△ADC。
A
4. 如图,在△ABC 中,D 为 BC 的中点. 若 AC = 3,AD = 4,则 AB 的长不可能是(

A.5
B.7
C.8
D.9
A
)
A.5
B.7
C.8
D.9
答案:A
解析:
证明:延长AD至点E,使DE=AD,连接BE。
∵D为BC中点,
∴BD=CD。
在△ADC和△EDB中,
$\left\{\begin{array}{l}AD=ED \\\angle ADC=\angle EDB \\CD=BD\end{array}\right.$
∴△ADC≌△EDB(SAS),
∴BE=AC=3。
∵AD=4,
∴AE=2AD=8。
在△ABE中,AE-BE<AB<AE+BE,
即8-3<AB<8+3,5<AB<11。
∴AB的长不可能是5。
A
∵D为BC中点,
∴BD=CD。
在△ADC和△EDB中,
$\left\{\begin{array}{l}AD=ED \\\angle ADC=\angle EDB \\CD=BD\end{array}\right.$
∴△ADC≌△EDB(SAS),
∴BE=AC=3。
∵AD=4,
∴AE=2AD=8。
在△ABE中,AE-BE<AB<AE+BE,
即8-3<AB<8+3,5<AB<11。
∴AB的长不可能是5。
A
5. 如图,在四边形 ABCD 中,对角线 AC,BD 相交于点 O,OA = OC,请你添加一个条件:

OB=OD(答案不唯一)
,使△AOB ≌ △COD.
答案:OB=OD(答案不唯一)
6. 如图,在△ABC 中,AD 为 BC 边的中线,BE ⊥ AD 于点 E,CF ⊥ AD 于点 F,若 AE = 6,AF = 2,则 DE =

2
.
答案:2
解析:
证明:
∵AD为BC边的中线,
∴BD=CD。
∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°。
在△BED和△CFD中,
∠BED=∠CFD,
∠BDE=∠CDF(对顶角相等),
BD=CD,
∴△BED≌△CFD(AAS)。
∴DE=DF。
∵AE=6,AF=2,
∴EF=AE-AF=6-2=4。
设DE=DF=x,则EF=DE+DF=2x=4,
解得x=2。
∴DE=2。
2
∵AD为BC边的中线,
∴BD=CD。
∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°。
在△BED和△CFD中,
∠BED=∠CFD,
∠BDE=∠CDF(对顶角相等),
BD=CD,
∴△BED≌△CFD(AAS)。
∴DE=DF。
∵AE=6,AF=2,
∴EF=AE-AF=6-2=4。
设DE=DF=x,则EF=DE+DF=2x=4,
解得x=2。
∴DE=2。
2
7. 如图,要测量水池宽 AB 的长度,可以从点 A 出发在地面上画一条线段 AC,使 AC ⊥ AB,再从点 C 观测,在 BA 的延长线上测得一点 D,使∠ACD = ∠ACB,这时量得 AD = 110 m,则水池宽 AB 的长度是
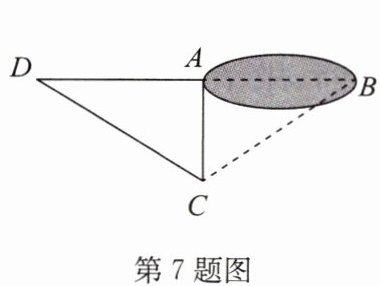
110
m.
答案:110
解析:
证明:
∵ $ AC \perp AB $,
∴ $ \angle CAD = \angle CAB = 90° $。
在 $ \triangle ACD $ 和 $ \triangle ACB $ 中,
$ \angle ACD = \angle ACB $(已知),
$ AC = AC $(公共边),
$ \angle CAD = \angle CAB $(已证),
∴ $ \triangle ACD \cong \triangle ACB $(ASA)。
∴ $ AD = AB $(全等三角形对应边相等)。
∵ $ AD = 110 \, m $,
∴ $ AB = 110 \, m $。
110
∵ $ AC \perp AB $,
∴ $ \angle CAD = \angle CAB = 90° $。
在 $ \triangle ACD $ 和 $ \triangle ACB $ 中,
$ \angle ACD = \angle ACB $(已知),
$ AC = AC $(公共边),
$ \angle CAD = \angle CAB $(已证),
∴ $ \triangle ACD \cong \triangle ACB $(ASA)。
∴ $ AD = AB $(全等三角形对应边相等)。
∵ $ AD = 110 \, m $,
∴ $ AB = 110 \, m $。
110
8. 如图,在四边形 ABCD 中,∠BAD = ∠C = 90°,AB = AD,AE ⊥ BC,垂足为 E. 若线段 AE = 2,则四边形 ABCD 的面积是

4
.
答案:4
解析:
过点D作DF⊥AE于点F,
∵∠BAD=90°,AE⊥BC,DF⊥AE,
∴∠BAE+∠DAF=90°,∠BAE+∠B=90°,
∴∠B=∠DAF,
∵AB=AD,∠AEB=∠DFA=90°,
∴△ABE≌△DAF(AAS),
∴BE=AF,AE=DF=2,
∵∠C=∠AEC=∠DFE=90°,
∴四边形CDFE是矩形,
∴EF=CD,CE=DF=2,
四边形ABCD面积=S△ABE+S△ADF+S矩形CDFE,
=2×(1/2)×AF×AE + EF×CE,
=AF×2 + EF×2,
=2(AF+EF)=2×AE=2×2=4.
4
∵∠BAD=90°,AE⊥BC,DF⊥AE,
∴∠BAE+∠DAF=90°,∠BAE+∠B=90°,
∴∠B=∠DAF,
∵AB=AD,∠AEB=∠DFA=90°,
∴△ABE≌△DAF(AAS),
∴BE=AF,AE=DF=2,
∵∠C=∠AEC=∠DFE=90°,
∴四边形CDFE是矩形,
∴EF=CD,CE=DF=2,
四边形ABCD面积=S△ABE+S△ADF+S矩形CDFE,
=2×(1/2)×AF×AE + EF×CE,
=AF×2 + EF×2,
=2(AF+EF)=2×AE=2×2=4.
4