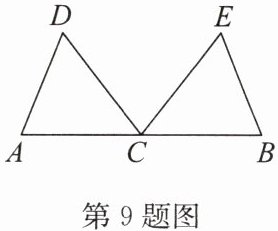
2025年启东中学作业本八年级数学上册苏科版宿迁专版第23页解析答案

9. 如图,C 是线段 AB 的中点,∠A = ∠B,∠ACE = ∠BCD. 求证：AD = BE.

答案：证明:
∵C是线段AB的中点,
∴AC=BC.
∵∠ACE=∠BCD,
∴∠ACE-∠DCE=∠BCD-∠DCE,即∠ACD=∠BCE.
又
∵∠A=∠B,
∴△ACD≌△BCE(ASA).
∴AD=BE.

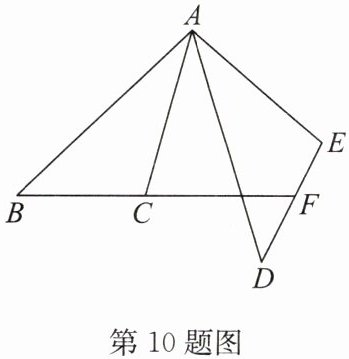
10. 如图,在△ABC 和△ADE 中,延长 BC 交 DE 于点 F. BC = DE,AC = AE,∠ACF + ∠E = 180°. 求证：AB = AD.

答案：证明:
∵∠ACB+∠ACF=180°,∠ACF+∠E=180°,
∴∠ACB=∠E.
在△ABC和△ADE中,$\left\{\begin{array}{l} BC=DE,\\ ∠ACB=∠E,\\ AC=AE,\end{array}\right. $
∴△ABC≌△ADE(SAS),
∴AB=AD.

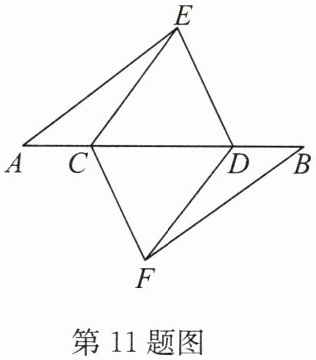
11. 如图,点 A,C,D,B 在同一条直线上,点 E,F 分别在直线 AB 的两侧,且 AE = BF,∠A = ∠B,CE // DF.
(1)求证：CE = DF；
(2)若 AB = 8,AC = 2,求 CD 的长.

答案：
(1)证明:
∵CE//DF,
∴∠ECD=∠FDC.
∵∠ECD+∠ACE=180°,∠FDC+∠FDB=180°,
∴∠ACE=∠BDF.
在△ACE与△BDF中,$\left\{\begin{array}{l} ∠ACE=∠BDF,\\ ∠A=∠B,\\ AE=BF,\end{array}\right. $
∴△ACE≌△BDF(AAS).
∴CE=DF.
(2)解:
∵△ACE≌△BDF,
∴BD=AC=2.
∵AB=8,
∴CD=AB-AC-BD=8-2-2=4.

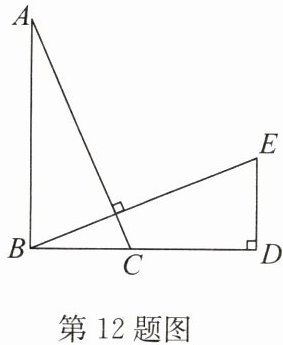
12. 如图,在 Rt△ABC 中,∠ABC = 90°,点 D 在 BC 边的延长线上,且 BD = AB. 过点 B 作 BE ⊥ AC,与 BD 的垂线 DE 交于点 E.
(1)求证：△ABC ≌ △BDE；
(2)请找出线段 AB,CD,DE 之间的数量关系,并说明理由.

答案：
(1)证明:
∵BE⊥AC,
∴∠A+∠ABE=90°.
∵∠ABC=90°,
∴∠DBE+∠ABE=90°,
∴∠A=∠DBE.
在△ABC和△BDE中,$\left\{\begin{array}{l} ∠A=∠DBE,\\ AB=BD,\\ ∠ABC=∠BDE,\end{array}\right. $
∴△ABC≌△BDE(ASA).
(2)解:AB=CD+DE.理由如下:
由
(1)知△ABC≌△BDE,
∴AB=BD,BC=DE.
∵BD=CD+BC,
∴AB=CD+DE.