1. 等边三角形 $ ABC $ 的两条中线 $ BD $ 和 $ CE $ 相交所夹钝角的度数为(
A.$ 60^{\circ} $
B.$ 90^{\circ} $
C.$ 120^{\circ} $
D.$ 150^{\circ} $
C
)A.$ 60^{\circ} $
B.$ 90^{\circ} $
C.$ 120^{\circ} $
D.$ 150^{\circ} $
答案:C
解析:
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,AB=BC=AC。
∵BD、CE是中线,
∴D、E分别是AC、AB中点,BD平分∠ABC,CE平分∠ACB,
∴∠DBC=∠ECB=30°。
在△BOC中,∠BOC=180°-∠DBC-∠ECB=180°-30°-30°=120°。
120°是钝角,
C
2. 下列条件中,不能判定 $ \triangle ABC $ 是等边三角形的是(
A.$ \angle A = \angle B = \angle C $
B.$ AB = AC $,$ \angle B = 60^{\circ} $
C.$ \angle A = 60^{\circ} $,$ \angle B = 60^{\circ} $
D.$ AB = AC $,且 $ \angle B = \angle C $
D
)A.$ \angle A = \angle B = \angle C $
B.$ AB = AC $,$ \angle B = 60^{\circ} $
C.$ \angle A = 60^{\circ} $,$ \angle B = 60^{\circ} $
D.$ AB = AC $,且 $ \angle B = \angle C $
答案:D
3. 如图,用圆规以直角顶点 $ O $ 为圆心,适当长为半径画一条弧交两直角边于 $ A $,$ B $ 两点,若再以点 $ A $ 为圆心,$ OA $ 长为半径画弧,与 $ \overset{\frown}{AB} $ 交于点 $ C $,则 $ \angle BOC = $

30°
.
答案:30°
解析:
解:连接 $OC$。
由题意,$OA=OB=OC$(均为圆的半径),且以点 $A$ 为圆心,$OA$ 长为半径画弧交 $\overset{\frown}{AB}$ 于点 $C$,则 $AC=OA$。
$\therefore OA=AC=OC$,$\triangle OAC$ 为等边三角形,$\angle AOC=60°$。
$\because \angle AOB=90°$,$\therefore \angle BOC=\angle AOB - \angle AOC=90° - 60°=30°$。
$30°$
由题意,$OA=OB=OC$(均为圆的半径),且以点 $A$ 为圆心,$OA$ 长为半径画弧交 $\overset{\frown}{AB}$ 于点 $C$,则 $AC=OA$。
$\therefore OA=AC=OC$,$\triangle OAC$ 为等边三角形,$\angle AOC=60°$。
$\because \angle AOB=90°$,$\therefore \angle BOC=\angle AOB - \angle AOC=90° - 60°=30°$。
$30°$
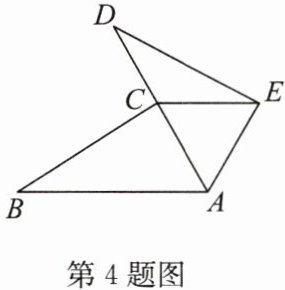
4. (2024·长沙)如图,点 $ C $ 在线段 $ AD $ 上,$ AB = AD $,$ \angle B = \angle D $,$ BC = DE $.
(1) 求证:$ \triangle ABC \cong \triangle ADE $;
(2) 若 $ \angle BAC = 60^{\circ} $,求 $ \angle ACE $ 的度数.
(1) 求证:$ \triangle ABC \cong \triangle ADE $;
(2) 若 $ \angle BAC = 60^{\circ} $,求 $ \angle ACE $ 的度数.

答案:
(1)证明:在$\triangle ABC$和$\triangle ADE$中
$\left\{\begin{array}{l} BC=DE,\\ ∠B=∠D,\\ AB=AD,\end{array}\right.$
$\therefore \triangle ABC\cong \triangle ADE(SAS).$
(2)解:由(1)得$\triangle ABC\cong \triangle ADE,$
$\therefore AC=AE,∠BAC=∠DAE=60^{\circ }.$
$\because ∠AEC=∠ACE,$
$\because ∠AEC+∠ACE=2∠ACE=180^{\circ }-∠DAE=120^{\circ },$
$\therefore ∠ACE=60^{\circ }.$
解析:
5. 如图,$ BD $ 是等边三角形 $ ABC $ 的边 $ AC $ 上的高,以点 $ D $ 为圆心,$ DB $ 长为半径作弧交 $ BC $ 的延长线于点 $ E $,则 $ \angle DEC = $(

A.$ 20^{\circ} $
B.$ 25^{\circ} $
C.$ 30^{\circ} $
D.$ 35^{\circ} $
C
)
A.$ 20^{\circ} $
B.$ 25^{\circ} $
C.$ 30^{\circ} $
D.$ 35^{\circ} $
答案:C
解析:
证明:
∵△ABC是等边三角形,BD是AC边上的高,
∴∠ABC=60°,BD平分∠ABC,
∴∠DBC=∠ABC/2=30°。
∵以D为圆心,DB为半径作弧交BC延长线于E,
∴DE=DB,
∴△DBE是等腰三角形,∠DEB=∠DBC=30°,
即∠DEC=30°。
C
∵△ABC是等边三角形,BD是AC边上的高,
∴∠ABC=60°,BD平分∠ABC,
∴∠DBC=∠ABC/2=30°。
∵以D为圆心,DB为半径作弧交BC延长线于E,
∴DE=DB,
∴△DBE是等腰三角形,∠DEB=∠DBC=30°,
即∠DEC=30°。
C
6. 如图,$ \angle AOB = 30^{\circ} $,$ OC $ 为 $ \angle AOB $ 内部一条射线,点 $ P $ 为射线 $ OC $ 上一点,$ OP = 6 $,$ M $,$ N $ 分别为 $ OA $,$ OB $ 边上的动点,则 $ \triangle MNP $ 周长的最小值为(

A.$ 6 $
B.$ 8 $
C.$ 12 $
D.$ 18 $
A
)
A.$ 6 $
B.$ 8 $
C.$ 12 $
D.$ 18 $
答案:A
解析:
解:作点 $ P $ 关于 $ OA $ 的对称点 $ P_1 $,关于 $ OB $ 的对称点 $ P_2 $,连接 $ P_1P_2 $,分别交 $ OA $、$ OB $ 于点 $ M $、$ N $,此时 $ \triangle MNP $ 周长最小,最小值为 $ P_1P_2 $ 的长。
由对称性质得:$ OP_1 = OP = 6 $,$ OP_2 = OP = 6 $,$ \angle P_1OA = \angle POA $,$ \angle P_2OB = \angle POB $。
因为 $ \angle AOB = 30° $,所以 $ \angle P_1OP_2 = 2\angle AOB = 60° $。
所以 $ \triangle P_1OP_2 $ 是等边三角形,因此 $ P_1P_2 = OP_1 = 6 $。
故 $ \triangle MNP $ 周长的最小值为 $ 6 $。
答案:A
由对称性质得:$ OP_1 = OP = 6 $,$ OP_2 = OP = 6 $,$ \angle P_1OA = \angle POA $,$ \angle P_2OB = \angle POB $。
因为 $ \angle AOB = 30° $,所以 $ \angle P_1OP_2 = 2\angle AOB = 60° $。
所以 $ \triangle P_1OP_2 $ 是等边三角形,因此 $ P_1P_2 = OP_1 = 6 $。
故 $ \triangle MNP $ 周长的最小值为 $ 6 $。
答案:A
7. (2024·宿城期末)如图,$ \angle AOB = 120^{\circ} $,$ OP $ 平分 $ \angle AOB $,且 $ OP = 1 $.若点 $ M $,$ N $ 分别在 $ OA $,$ OB $ 上,且 $ \triangle PMN $ 为等边三角形,则满足上述条件的 $ \triangle PMN $ 有(

A.$ 1 $ 个
B.$ 2 $ 个
C.$ 3 $ 个
D.无数个
D
)
A.$ 1 $ 个
B.$ 2 $ 个
C.$ 3 $ 个
D.无数个
答案:D
解析:
解:
∵∠AOB=120°,OP平分∠AOB,
∴∠AOP=∠BOP=60°,OP=1。
在OA、OB上分别取点M、N,使OM=ON=t(t>0),连接PM、PN、MN。
当t变化时,可构造不同的等边△PMN:
1. 当M、N在射线OA、OB正方向上,且PM=PN=MN时,存在等边三角形;
2. 随着t的增大或减小,通过旋转或缩放可得到无数组满足条件的M、N点,使△PMN为等边三角形。
综上,满足条件的△PMN有无数个。
答案:D
∵∠AOB=120°,OP平分∠AOB,
∴∠AOP=∠BOP=60°,OP=1。
在OA、OB上分别取点M、N,使OM=ON=t(t>0),连接PM、PN、MN。
当t变化时,可构造不同的等边△PMN:
1. 当M、N在射线OA、OB正方向上,且PM=PN=MN时,存在等边三角形;
2. 随着t的增大或减小,通过旋转或缩放可得到无数组满足条件的M、N点,使△PMN为等边三角形。
综上,满足条件的△PMN有无数个。
答案:D
8. 已知 $ \triangle ABC $ 是等边三角形,点 $ D $,$ E $ 分别在 $ AC $,$ BC $ 上,且 $ CD = BE $,则 $ \angle AFD = $ __

60°
__.
答案:60°
解析:
证明:
∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠C=60°.
在△ABE和△BCD中,
$\begin{cases}AB=BC, \\\angle ABE=\angle C=60°, \\BE=CD,\end{cases}$
∴△ABE≌△BCD(SAS).
∴∠BAE=∠CBD.
∵∠AFD是△ABF的外角,
∴∠AFD=∠ABF+∠BAE=∠ABF+∠CBD=∠ABC=60°.
60°
∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠C=60°.
在△ABE和△BCD中,
$\begin{cases}AB=BC, \\\angle ABE=\angle C=60°, \\BE=CD,\end{cases}$
∴△ABE≌△BCD(SAS).
∴∠BAE=∠CBD.
∵∠AFD是△ABF的外角,
∴∠AFD=∠ABF+∠BAE=∠ABF+∠CBD=∠ABC=60°.
60°