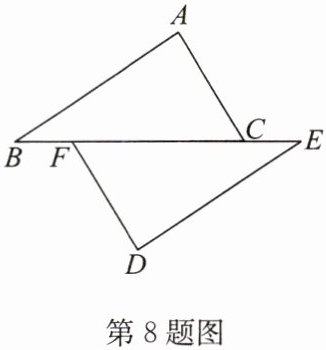
8. 如图,$\triangle ABC\cong\triangle DEF$,$BE = 5$,$BF = 1$,则$CF = $
3
。
答案:3
解析:
解:
∵△ABC≌△DEF,
∴BC=EF。
∵BE=5,BF=1,
∴EF=BE-BF-CF=5-1-CF=4-CF,
BC=BF+CF=1+CF。
∵BC=EF,
∴1+CF=4-CF,
解得CF=3。
故答案为:3。
∵△ABC≌△DEF,
∴BC=EF。
∵BE=5,BF=1,
∴EF=BE-BF-CF=5-1-CF=4-CF,
BC=BF+CF=1+CF。
∵BC=EF,
∴1+CF=4-CF,
解得CF=3。
故答案为:3。
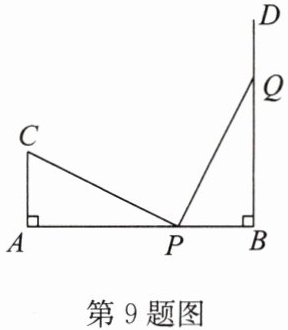
9. 如图,$AB = 12$,$CA\perp AB于点A$,$DB\perp AB于点B$,且$AC = 4$,点$P在线段AB$上,点$Q在射线BD$上。若$\triangle CAP与\triangle PQB$全等,则$AP = $
8或6
。
答案:8或6
解析:
解:设$AP = x$,则$PB=12 - x$。
情况1:$\triangle CAP \cong \triangle PBQ$
$\because CA\perp AB$,$DB\perp AB$
$\therefore \angle A = \angle B = 90°$
$\therefore AC = PB$,$AP = BQ$
$\because AC = 4$
$\therefore 4 = 12 - x$
解得$x = 8$
情况2:$\triangle CAP \cong \triangle QBP$
$\therefore AC = QB$,$AP = BP$
$\because AP = BP$
$\therefore x = 12 - x$
解得$x = 6$
综上,$AP = 8$或$6$
答案:8或6
情况1:$\triangle CAP \cong \triangle PBQ$
$\because CA\perp AB$,$DB\perp AB$
$\therefore \angle A = \angle B = 90°$
$\therefore AC = PB$,$AP = BQ$
$\because AC = 4$
$\therefore 4 = 12 - x$
解得$x = 8$
情况2:$\triangle CAP \cong \triangle QBP$
$\therefore AC = QB$,$AP = BP$
$\because AP = BP$
$\therefore x = 12 - x$
解得$x = 6$
综上,$AP = 8$或$6$
答案:8或6
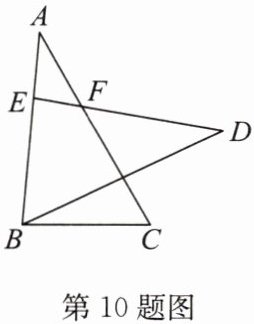
10. 如图,已知$\triangle ABC\cong\triangle DEB$,点$E在边AB$上,$DE与AC相交于点F$。
(1) 当$DE = 9$,$BC = 5$时,线段$AE$的长为
(2) 已知$\angle D = 35^{\circ}$,$\angle C = 60^{\circ}$,求$\angle DBC$的度数。
(1) 当$DE = 9$,$BC = 5$时,线段$AE$的长为
4
;(2) 已知$\angle D = 35^{\circ}$,$\angle C = 60^{\circ}$,求$\angle DBC$的度数。

(2)解:
∵△ABC≌△DEB,
∴∠A=∠D=35°,∠DBE=∠C=60°,
∴∠ABC=180°−∠A−∠C=85°.
∴∠DBC=∠ABC−∠DBE=85°−60°=25°.
∵△ABC≌△DEB,
∴∠A=∠D=35°,∠DBE=∠C=60°,
∴∠ABC=180°−∠A−∠C=85°.
∴∠DBC=∠ABC−∠DBE=85°−60°=25°.
答案:
(1)4
(2)解:
∵△ABC≌△DEB,
∴∠A=∠D=35°,∠DBE=∠C=60°,
∴∠ABC=180°−∠A−∠C=85°.
∴∠DBC=∠ABC−∠DBE=85°−60°=25°.
(1)4
(2)解:
∵△ABC≌△DEB,
∴∠A=∠D=35°,∠DBE=∠C=60°,
∴∠ABC=180°−∠A−∠C=85°.
∴∠DBC=∠ABC−∠DBE=85°−60°=25°.
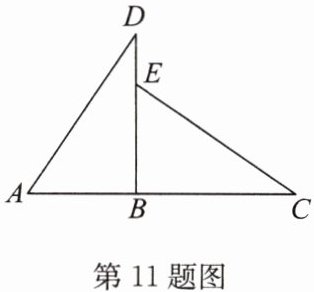
11. 如图,点$A$,$B$,$C$在同一条直线上,$\triangle ABD\cong\triangle EBC$,点$E在BD$边上,$AB = 2\mathrm{cm}$,$BC = 3\mathrm{cm}$。
(1) 求$DE$的长;
(2) 判断$BD所在直线与AC$所在直线的位置关系,并说明理由;
(3) 判断$AD所在直线与CE$所在直线的位置关系,并说明理由。
(1) 求$DE$的长;
(2) 判断$BD所在直线与AC$所在直线的位置关系,并说明理由;
(3) 判断$AD所在直线与CE$所在直线的位置关系,并说明理由。

答案:
(1)
∵△ABD≌△EBC,
∴BD=BC=3cm,BE=AB=2cm,
∴DE=BD−BE=3−2=1(cm).
(2)BD所在直线与AC所在直线垂直,理由如下:
∵△ABD≌△EBC,
∴∠ABD=∠EBC;又
∵点A,B,C在同一条直线上,
∴∠EBC=90°,
∴BD所在直线与AC所在直线垂直.
(3)AD所在直线与CE所在直线垂直.理由如下:如答图,延长CE交AD于点F.
∵△ABD≌△EBC,
∴∠D=∠C;由
(2)知∠EBC=∠EBA=90°,
∴在Rt△ABD中,∠A+∠D=90°,
∴∠A+∠C=90°,
∴∠AFC=90°,
∴AD所在直线与CE所在直线垂直.
(1)
∵△ABD≌△EBC,
∴BD=BC=3cm,BE=AB=2cm,
∴DE=BD−BE=3−2=1(cm).
(2)BD所在直线与AC所在直线垂直,理由如下:
∵△ABD≌△EBC,
∴∠ABD=∠EBC;又
∵点A,B,C在同一条直线上,
∴∠EBC=90°,
∴BD所在直线与AC所在直线垂直.
(3)AD所在直线与CE所在直线垂直.理由如下:如答图,延长CE交AD于点F.
∵△ABD≌△EBC,
∴∠D=∠C;由
(2)知∠EBC=∠EBA=90°,
∴在Rt△ABD中,∠A+∠D=90°,
∴∠A+∠C=90°,
∴∠AFC=90°,
∴AD所在直线与CE所在直线垂直.