7. 已知 $ A(0,2) $,$ B(1,0) $,点 $ P $ 在 $ x $ 轴上,且 $ \triangle PAB $ 的面积为 $ 5 $,则点 $ P $ 的坐标为(
A.$ (6,0) $
B.$ (-4,0) $
C.$ (6,0) $ 或 $ (-4,0) $
D.无法确定
C
)A.$ (6,0) $
B.$ (-4,0) $
C.$ (6,0) $ 或 $ (-4,0) $
D.无法确定
答案:C
解析:
设点$ P $的坐标为$ (x,0) $。
因为点$ B(1,0) $在$ x $轴上,所以$ PB = |x - 1| $。
点$ A(0,2) $到$ x $轴的距离为$ 2 $,即$ \triangle PAB $中$ PB $边上的高为$ 2 $。
根据三角形面积公式$ S = \frac{1}{2} × 底 × 高 $,可得:
$\frac{1}{2} × |x - 1| × 2 = 5$
化简得:
$|x - 1| = 5$
当$ x - 1 = 5 $时,$ x = 6 $;当$ x - 1 = -5 $时,$ x = -4 $。
所以点$ P $的坐标为$ (6,0) $或$ (-4,0) $。
C
因为点$ B(1,0) $在$ x $轴上,所以$ PB = |x - 1| $。
点$ A(0,2) $到$ x $轴的距离为$ 2 $,即$ \triangle PAB $中$ PB $边上的高为$ 2 $。
根据三角形面积公式$ S = \frac{1}{2} × 底 × 高 $,可得:
$\frac{1}{2} × |x - 1| × 2 = 5$
化简得:
$|x - 1| = 5$
当$ x - 1 = 5 $时,$ x = 6 $;当$ x - 1 = -5 $时,$ x = -4 $。
所以点$ P $的坐标为$ (6,0) $或$ (-4,0) $。
C
8. 如图,将正方形 $ OEFG $ 放在平面直角坐标系中,$ O $ 是坐标原点,点 $ E $ 的坐标为 $ (2,3) $,则点 $ F $ 的坐标为
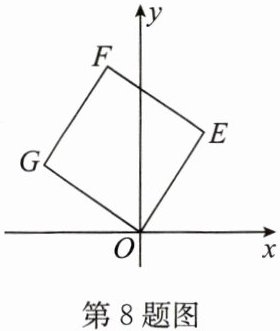
(-1,5)
.
答案:(-1,5)
解析:
解:过点E作EH⊥x轴于H,过点F作FM⊥y轴于M,连接OF,EG交于点N。
∵四边形OEFG是正方形,
∴N为EG,OF中点,ON=NF,EG⊥OF。
∵E(2,3),
∴H(2,0),EH=3,OH=2。
∴EG中点N的坐标为(1, 3/2)。
设F(x,y),则OF中点N的坐标为(x/2, y/2)。
∴x/2=1,y/2=3/2,解得x=2,y=3(此为E点,舍去)。
考虑向量法,向量OE=(2,3),则向量OG=(-3,2)(正方形邻边垂直且等长)。
∴G点坐标为(-3,2)。
∵F=E+G-O,
∴F(2-3, 3+2)=(-1,5)。
(-1,5)
∵四边形OEFG是正方形,
∴N为EG,OF中点,ON=NF,EG⊥OF。
∵E(2,3),
∴H(2,0),EH=3,OH=2。
∴EG中点N的坐标为(1, 3/2)。
设F(x,y),则OF中点N的坐标为(x/2, y/2)。
∴x/2=1,y/2=3/2,解得x=2,y=3(此为E点,舍去)。
考虑向量法,向量OE=(2,3),则向量OG=(-3,2)(正方形邻边垂直且等长)。
∴G点坐标为(-3,2)。
∵F=E+G-O,
∴F(2-3, 3+2)=(-1,5)。
(-1,5)
9. 如图为某战役中缴获的敌人防御工事坐标地图的碎片,依稀可见,一号暗堡的坐标为 $ (1,2) $,二号暗堡的坐标为 $ (-3,2) $. 另有情报得知,指挥部的坐标为 $ (-1,-2) $,你能在图上标出指挥部的位置 $ P $ 吗?试通过画图加以说明.
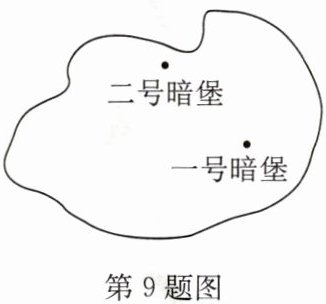

答案:
解:如答图,连接AB并将其四等分,在线段AB上取点M,使AM=$\frac{1}{4}$AB,过点M作直线OM⊥AB,使OM=2AM,以O点为坐标原点,OM所在的直线为y轴建立平面直角坐标系,便可求得点P的位置了.
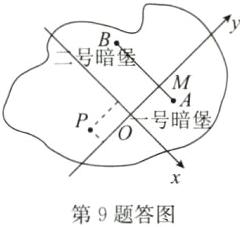
解:如答图,连接AB并将其四等分,在线段AB上取点M,使AM=$\frac{1}{4}$AB,过点M作直线OM⊥AB,使OM=2AM,以O点为坐标原点,OM所在的直线为y轴建立平面直角坐标系,便可求得点P的位置了.

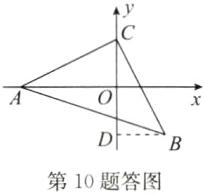
10. 如图,在平面直角坐标系中,$ A(-4,0) $,$ C $ 是 $ y $ 轴正半轴上的一点,且 $ \angle ACB = 90^{\circ} $,$ AC = BC $. 若点 $ B $ 在第四象限,$ C(0,2) $,求点 $ B $ 的坐标.
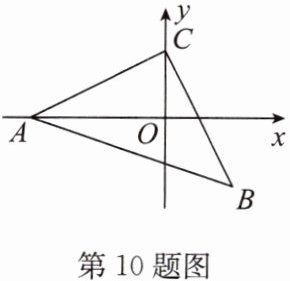

答案:
解:如答图,过点B作BD⊥y轴于点D,则∠BDC=∠AOC = 90°.
∵A(-4,0),C(0,2),
∴OA = 4,OC = 2.
∵∠ACB = 90°,
∴∠ACO + ∠DCB = ∠ACO + ∠OAC = 90°,
∴∠OAC = ∠DCB.
又
∵AC = BC,
∴△AOC≌△CDB(AAS).
∴CD = OA = 4,BD = OC = 2.
∴OD = CD - OC = 4 - 2 = 2.
又
∵点B在第四象限,
∴B(2,-2).
解:如答图,过点B作BD⊥y轴于点D,则∠BDC=∠AOC = 90°.

∵A(-4,0),C(0,2),
∴OA = 4,OC = 2.
∵∠ACB = 90°,
∴∠ACO + ∠DCB = ∠ACO + ∠OAC = 90°,
∴∠OAC = ∠DCB.
又
∵AC = BC,
∴△AOC≌△CDB(AAS).
∴CD = OA = 4,BD = OC = 2.
∴OD = CD - OC = 4 - 2 = 2.
又
∵点B在第四象限,
∴B(2,-2).
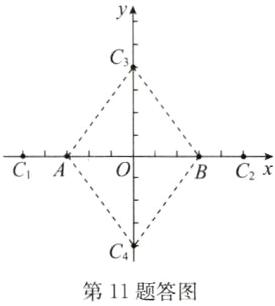
11. 在平面直角坐标系中,已知点 $ A(-3,0) $,$ B(3,0) $,点 $ C $ 在坐标轴上,且 $ AC + BC = 10 $,求出满足条件的所有点 $ C $ 的坐标.
答案:
解:如答图,若点C在x轴上,设C(x,0).当点C在点A的左侧时,-3 - x + 3 - x = 10,解得x = -5;当点C在点A的右侧时,x - (-3) + x - 3 = 10,解得x = 5.若点C在y轴上,设C(0,y),易知AC = BC = 5,由OA = OB = 3,根据勾股定理,求得OC = 4,此时C(0,4)或C(0,-4).综上,满足条件的点C有4个,其坐标分别为(-5,0),(5,0),(0,4),(0,-4).
解:如答图,若点C在x轴上,设C(x,0).当点C在点A的左侧时,-3 - x + 3 - x = 10,解得x = -5;当点C在点A的右侧时,x - (-3) + x - 3 = 10,解得x = 5.若点C在y轴上,设C(0,y),易知AC = BC = 5,由OA = OB = 3,根据勾股定理,求得OC = 4,此时C(0,4)或C(0,-4).综上,满足条件的点C有4个,其坐标分别为(-5,0),(5,0),(0,4),(0,-4).
