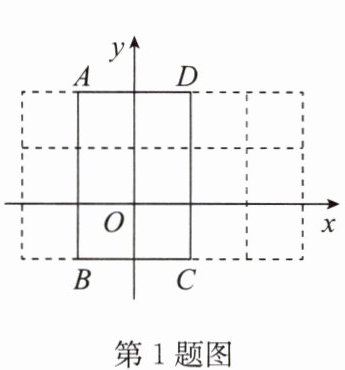
1. (2024·南通崇川区期末)如图,在平面直角坐标系中,长方形 $ABCD$ 的四个顶点坐标分别为 $A(-1,2)$,$B(-1,-1)$,$C(1,-1)$,$D(1,2)$,点 $P$ 从点 $A$ 出发,沿长方形的边顺时针运动,速度为每秒 $2$ 个长度单位,点 $Q$ 从点 $A$ 出发,沿长方形的边逆时针运动,速度为每秒 $3$ 个长度单位. 记 $P$,$Q$ 在长方形边上第 $1$ 次相遇时的点为 $M_1$,第二次相遇时的点为 $M_2$,第三次相遇时的点为 $M_3$,……$$,则点 $M_{2024}$ 的坐标为(
A.$(1,0)$
B.$(-1,0)$
C.$(1,2)$
D.$(0,-1)$
D
)
A.$(1,0)$
B.$(-1,0)$
C.$(1,2)$
D.$(0,-1)$
答案:D
解析:
解:长方形ABCD的长为$1 - (-1) = 2$,宽为$2 - (-1) = 3$,周长为$2×(2 + 3) = 10$。
设运动时间为$t$秒,P、Q第一次相遇时,共运动了10个单位,可得$2t + 3t = 10$,解得$t = 2$。
P运动路程:$2×2 = 4$,从A(-1,2)顺时针:A到B(3个单位),再向右1个单位,得$M_1(0,-1)$。
第二次相遇共运动20个单位,$2t + 3t = 20$,$t = 4$。
P运动路程:$2×4 = 8$,A到B
(3)→B到C
(2)→C到D
(3),共8个单位,得$M_2(1,2)$。
第三次相遇共运动30个单位,$t = 6$,P运动路程:$2×6 = 12$,周长10,12 - 10 = 2,A到B
(3)未到,从A向下2个单位,得$M_3(-1,0)$。
第四次相遇共运动40个单位,$t = 8$,P运动路程:$2×8 = 16$,16 - 10 = 6,A→B
(3)→B→C
(2)→C→D
(1),得$M_4(1,1)$。
第五次相遇共运动50个单位,$t = 10$,P运动路程:$2×10 = 20$,20 - 2×10 = 0,回到A(-1,2),$M_5(-1,2)$。
第六次相遇共运动60个单位,$t = 12$,P运动路程:$2×12 = 24$,24 - 2×10 = 4,与第一次相遇位置相同,周期为4。
$2024÷4 = 506$,整除,$M_{2024}$与$M_4$位置不同,继续计算:
$M_1(0,-1)$,$M_2(1,2)$,$M_3(-1,0)$,$M_4(1,0)$,$M_5(-1,2)$,$M_6(0,-1)$,周期为4。
$2024÷4 = 506$,$M_{2024}$与$M_4$一致,$M_4(1,0)$。
答案:A
设运动时间为$t$秒,P、Q第一次相遇时,共运动了10个单位,可得$2t + 3t = 10$,解得$t = 2$。
P运动路程:$2×2 = 4$,从A(-1,2)顺时针:A到B(3个单位),再向右1个单位,得$M_1(0,-1)$。
第二次相遇共运动20个单位,$2t + 3t = 20$,$t = 4$。
P运动路程:$2×4 = 8$,A到B
(3)→B到C
(2)→C到D
(3),共8个单位,得$M_2(1,2)$。
第三次相遇共运动30个单位,$t = 6$,P运动路程:$2×6 = 12$,周长10,12 - 10 = 2,A到B
(3)未到,从A向下2个单位,得$M_3(-1,0)$。
第四次相遇共运动40个单位,$t = 8$,P运动路程:$2×8 = 16$,16 - 10 = 6,A→B
(3)→B→C
(2)→C→D
(1),得$M_4(1,1)$。
第五次相遇共运动50个单位,$t = 10$,P运动路程:$2×10 = 20$,20 - 2×10 = 0,回到A(-1,2),$M_5(-1,2)$。
第六次相遇共运动60个单位,$t = 12$,P运动路程:$2×12 = 24$,24 - 2×10 = 4,与第一次相遇位置相同,周期为4。
$2024÷4 = 506$,整除,$M_{2024}$与$M_4$位置不同,继续计算:
$M_1(0,-1)$,$M_2(1,2)$,$M_3(-1,0)$,$M_4(1,0)$,$M_5(-1,2)$,$M_6(0,-1)$,周期为4。
$2024÷4 = 506$,$M_{2024}$与$M_4$一致,$M_4(1,0)$。
答案:A
2. 如图,在平面直角坐标系中,一动点从原点 $O$ 出发,按向上、向右、向下、向右的方向不断地移动,每次移动 $1$ 个单位长度,得到点 $A_1(0,1)$,$A_2(1,1)$,$A_3(1,0)$,$A_4(2,0)$,…$$,则点 $A_{2022}$ 的坐标为(

A.$(1011,0)$
B.$(1011,1)$
C.$(2022,0)$
D.$(2022,1)$
B
)
A.$(1011,0)$
B.$(1011,1)$
C.$(2022,0)$
D.$(2022,1)$
答案:B
解析:
解:观察点的坐标规律:
$A_1(0,1)$,$A_2(1,1)$,$A_3(1,0)$,$A_4(2,0)$;
$A_5(2,1)$,$A_6(3,1)$,$A_7(3,0)$,$A_8(4,0)$;
每4个点为一组,每组横坐标增加2,纵坐标按$1,1,0,0$循环。
计算组数与余数:$2022÷4=505$余$2$。
每组第2个点的坐标特征:横坐标为$2×505 + 1=1011$,纵坐标为$1$。
故点$A_{2022}$的坐标为$(1011,1)$。
B
$A_1(0,1)$,$A_2(1,1)$,$A_3(1,0)$,$A_4(2,0)$;
$A_5(2,1)$,$A_6(3,1)$,$A_7(3,0)$,$A_8(4,0)$;
每4个点为一组,每组横坐标增加2,纵坐标按$1,1,0,0$循环。
计算组数与余数:$2022÷4=505$余$2$。
每组第2个点的坐标特征:横坐标为$2×505 + 1=1011$,纵坐标为$1$。
故点$A_{2022}$的坐标为$(1011,1)$。
B
3. 如图,正方形 $ABCD$ 的顶点 $A(1,1)$,$B(3,1)$,规定把正方形 $ABCD$“先沿 $x$ 轴翻折,再向左平移 $1$ 个单位长度”为一次变换,这样连续经过 $2023$ 次变换后,正方形 $ABCD$ 的顶点 $C$ 的坐标为(

A.$(-2022,-3)$
B.$(-2022,3)$
C.$(-2020,-3)$
D.$(-2020,3)$
C
)
A.$(-2022,-3)$
B.$(-2022,3)$
C.$(-2020,-3)$
D.$(-2020,3)$
答案:C
解析:
解:
∵正方形$ABCD$顶点$A(1,1)$,$B(3,1)$,
∴$AB=2$,$C(3,3)$。
一次变换:
沿$x$轴翻折:$C(3,3)\to(3,-3)$;
向左平移1个单位:$(3,-3)\to(2,-3)$。
二次变换:
沿$x$轴翻折:$(2,-3)\to(2,3)$;
向左平移1个单位:$(2,3)\to(1,3)$。
三次变换:
沿$x$轴翻折:$(1,3)\to(1,-3)$;
向左平移1个单位:$(1,-3)\to(0,-3)$。
规律:
奇数次变换后,纵坐标为$-3$;
横坐标:每次变换向左平移1个单位,$n$次变换后横坐标为$3 - n$。
2023次变换(奇数):
横坐标:$3 - 2023 = -2020$,纵坐标:$-3$。
∴顶点$C$坐标为$(-2020,-3)$。
答案:$C$
∵正方形$ABCD$顶点$A(1,1)$,$B(3,1)$,
∴$AB=2$,$C(3,3)$。
一次变换:
沿$x$轴翻折:$C(3,3)\to(3,-3)$;
向左平移1个单位:$(3,-3)\to(2,-3)$。
二次变换:
沿$x$轴翻折:$(2,-3)\to(2,3)$;
向左平移1个单位:$(2,3)\to(1,3)$。
三次变换:
沿$x$轴翻折:$(1,3)\to(1,-3)$;
向左平移1个单位:$(1,-3)\to(0,-3)$。
规律:
奇数次变换后,纵坐标为$-3$;
横坐标:每次变换向左平移1个单位,$n$次变换后横坐标为$3 - n$。
2023次变换(奇数):
横坐标:$3 - 2023 = -2020$,纵坐标:$-3$。
∴顶点$C$坐标为$(-2020,-3)$。
答案:$C$
4. (2024·常州金坛区期末)在如图所示的平面直角坐标系中,$\triangle OA_1B_1$ 是边长为 $4$ 的等边三角形,作 $\triangle B_2A_2B_1$ 与 $\triangle OA_1B_1$ 关于点 $B_1$ 成中心对称,再作 $\triangle B_2A_3B_3$ 与 $\triangle B_2A_2B_1$ 关于点 $B_2$ 成中心对称,……$$ 如此下去,则 $\triangle B_{2n}A_{2n + 1}B_{2n + 1}$($n$ 是正整数)的顶点 $A_{2n + 1}$ 的坐标是(

A.$(8n + 2,2\sqrt{3})$
B.$(8n - 2,2\sqrt{3})$
C.$(4n + 1,\sqrt{3})$
D.$(4n - 1,\sqrt{3})$
A
)
A.$(8n + 2,2\sqrt{3})$
B.$(8n - 2,2\sqrt{3})$
C.$(4n + 1,\sqrt{3})$
D.$(4n - 1,\sqrt{3})$
答案:A
解析:
解:
$\triangle OA_1B_1$为等边三角形,边长为$4$,则$O(0,0)$,$B_1(4,0)$。
$A_1$的横坐标为$\frac{0+4}{2}=2$,纵坐标为$\sqrt{4^2-2^2}=2\sqrt{3}$,即$A_1(2,2\sqrt{3})$。
$\triangle B_2A_2B_1$与$\triangle OA_1B_1$关于$B_1$中心对称,设$B_2(x,0)$,由中心对称性质:$\frac{0+x}{2}=4$,得$x=8$,即$B_2(8,0)$。$A_2$与$A_1$关于$B_1$对称,坐标为$(6,-2\sqrt{3})$。
$\triangle B_2A_3B_3$与$\triangle B_2A_2B_1$关于$B_2$中心对称,设$B_3(y,0)$,则$\frac{4+y}{2}=8$,得$y=12$,即$B_3(12,0)$。$A_3$与$A_2$关于$B_2$对称,坐标为$(10,2\sqrt{3})$。
观察$A_1(2,2\sqrt{3})$,$A_3(10,2\sqrt{3})$,横坐标规律:$2=8×1-6$($n=1$时),$10=8×2-6$($n=2$时),推测$A_{2n+1}$横坐标为$8n-6+8=8n+2$,纵坐标恒为$2\sqrt{3}$。
故$\triangle B_{2n}A_{2n+1}B_{2n+1}$中$A_{2n+1}$的坐标为$(8n+2,2\sqrt{3})$。
答案:A
$\triangle OA_1B_1$为等边三角形,边长为$4$,则$O(0,0)$,$B_1(4,0)$。
$A_1$的横坐标为$\frac{0+4}{2}=2$,纵坐标为$\sqrt{4^2-2^2}=2\sqrt{3}$,即$A_1(2,2\sqrt{3})$。
$\triangle B_2A_2B_1$与$\triangle OA_1B_1$关于$B_1$中心对称,设$B_2(x,0)$,由中心对称性质:$\frac{0+x}{2}=4$,得$x=8$,即$B_2(8,0)$。$A_2$与$A_1$关于$B_1$对称,坐标为$(6,-2\sqrt{3})$。
$\triangle B_2A_3B_3$与$\triangle B_2A_2B_1$关于$B_2$中心对称,设$B_3(y,0)$,则$\frac{4+y}{2}=8$,得$y=12$,即$B_3(12,0)$。$A_3$与$A_2$关于$B_2$对称,坐标为$(10,2\sqrt{3})$。
观察$A_1(2,2\sqrt{3})$,$A_3(10,2\sqrt{3})$,横坐标规律:$2=8×1-6$($n=1$时),$10=8×2-6$($n=2$时),推测$A_{2n+1}$横坐标为$8n-6+8=8n+2$,纵坐标恒为$2\sqrt{3}$。
故$\triangle B_{2n}A_{2n+1}B_{2n+1}$中$A_{2n+1}$的坐标为$(8n+2,2\sqrt{3})$。
答案:A