10. (2024·常州武进区一模)如图,动点 $ P $ 在平面直角坐标系中,沿曲线的方向从左往右运动,第 $ 1 $ 秒从原点运动到点 $ (1,1) $,第 $ 2 $ 秒运动到点 $ (2,0) $,第 $ 3 $ 秒运动到点 $ (3,-1) $,第 $ 4 $ 秒运动到点 $ (4,0) … … $ 照这样的规律,第 $ 2024 $ 秒运动到点______。


答案:(2024,0)
解析:
解:由题意可知,动点 $ P $ 的运动规律为:
第 $ 1 $ 秒:$(1,1)$
第 $ 2 $ 秒:$(2,0)$
第 $ 3 $ 秒:$(3,-1)$
第 $ 4 $ 秒:$(4,0)$
第 $ 5 $ 秒:$(5,1)$
第 $ 6 $ 秒:$(6,0)$
第 $ 7 $ 秒:$(7,-1)$
第 $ 8 $ 秒:$(8,0)$
……
观察可得,横坐标为运动时间 $ t $,纵坐标以 $ 1,0,-1,0 $ 为一个周期循环,周期为 $ 4 $。
因为 $ 2024 ÷ 4 = 506 $,余数为 $ 0 $,所以第 $ 2024 $ 秒时,纵坐标对应周期中的第 $ 4 $ 个位置,即 $ 0 $。
故第 $ 2024 $ 秒运动到点 $(2024,0)$。
$(2024,0)$
第 $ 1 $ 秒:$(1,1)$
第 $ 2 $ 秒:$(2,0)$
第 $ 3 $ 秒:$(3,-1)$
第 $ 4 $ 秒:$(4,0)$
第 $ 5 $ 秒:$(5,1)$
第 $ 6 $ 秒:$(6,0)$
第 $ 7 $ 秒:$(7,-1)$
第 $ 8 $ 秒:$(8,0)$
……
观察可得,横坐标为运动时间 $ t $,纵坐标以 $ 1,0,-1,0 $ 为一个周期循环,周期为 $ 4 $。
因为 $ 2024 ÷ 4 = 506 $,余数为 $ 0 $,所以第 $ 2024 $ 秒时,纵坐标对应周期中的第 $ 4 $ 个位置,即 $ 0 $。
故第 $ 2024 $ 秒运动到点 $(2024,0)$。
$(2024,0)$
11. 在平面直角坐标系中,已知点 $ M $ 的坐标为 $ (3m - 2,5 - 2m) $。
(1) 若点 $ M $ 到 $ x $ 轴的距离是 $ 3 $,求 $ m $ 的值。
(2) 若点 $ M $ 在第二、四象限的角平分线上,求 $ m $ 的值。
(3) 若点 $ M $ 在第一象限的角平分线上,求点 $ M $ 关于原点对称点 $ N $ 的坐标。
(4) 判断点 $ M $ 是否可能在第三象限,若可能,求出 $ m $ 的取值范围;若不可能,请说明理由。
(1) 若点 $ M $ 到 $ x $ 轴的距离是 $ 3 $,求 $ m $ 的值。
(2) 若点 $ M $ 在第二、四象限的角平分线上,求 $ m $ 的值。
(3) 若点 $ M $ 在第一象限的角平分线上,求点 $ M $ 关于原点对称点 $ N $ 的坐标。
(4) 判断点 $ M $ 是否可能在第三象限,若可能,求出 $ m $ 的取值范围;若不可能,请说明理由。
答案:解:
(1)由题意,得$|5-2m|=3$,解得$m=1$或4.
∴m的值为1或4.
(2)由题意,得$3m-2+5-2m=0$,解得$m=-3.$
∴m的值为-3.
(3)由题意,得$3m-2=5-2m$,解得$m=\frac {7}{5}$,此时$M(\frac {11}{5},\frac {11}{5}).$
∵点M,N关于原点对称,
∴$N(-\frac {11}{5},-\frac {11}{5}).$
(4)点M不可能在第三象限.理由:若点M在第三象限,则$\left\{\begin{array}{l} 3m-2<0,\\ 5-2m<0,\end{array}\right. $即$\left\{\begin{array}{l} m<\frac {2}{3},\\ m>\frac {5}{2},\end{array}\right. $而此不等式组无解,故点M不可能在第三象限.
(1)由题意,得$|5-2m|=3$,解得$m=1$或4.
∴m的值为1或4.
(2)由题意,得$3m-2+5-2m=0$,解得$m=-3.$
∴m的值为-3.
(3)由题意,得$3m-2=5-2m$,解得$m=\frac {7}{5}$,此时$M(\frac {11}{5},\frac {11}{5}).$
∵点M,N关于原点对称,
∴$N(-\frac {11}{5},-\frac {11}{5}).$
(4)点M不可能在第三象限.理由:若点M在第三象限,则$\left\{\begin{array}{l} 3m-2<0,\\ 5-2m<0,\end{array}\right. $即$\left\{\begin{array}{l} m<\frac {2}{3},\\ m>\frac {5}{2},\end{array}\right. $而此不等式组无解,故点M不可能在第三象限.
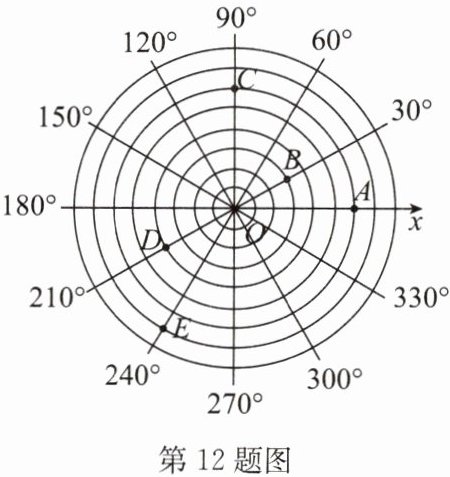
12. (2024·宿豫期末)【阅读理解】画一条水平数轴,记为 $ x $ 轴,以原点 $ O $ 为圆心,过 $ x $ 轴上的每一刻度点画同心圆,过原点 $ O $ 按逆时针方向画与 $ x $ 轴正半轴的角度分别为 $ 30^{\circ} $,$ 60^{\circ} $,$ 90^{\circ} $,$ 120^{\circ} $,$ 150^{\circ} $,…$ $,$ 330^{\circ} $ 的射线,这样就建立了“圆”坐标系。如图,在建立的“圆”坐标系内,我们可以将点 $ A $,$ B $,$ D $ 的坐标分别表示为 $ (6,0^{\circ}) $,$ (3,30^{\circ}) $,$ (4,210^{\circ}) $。
【问题探究】
(1) 点 $ C $,$ E $ 的坐标分别为______,______;
(2) 在“圆”坐标系内描出点 $ F(6,120^{\circ}) $,$ G(3,150^{\circ}) $,连接 $ AB $,$ FG $,试说明 $ \triangle AOB \cong \triangle FOG $;
(3) 若 $ \triangle OAP $ 是等边三角形,则点 $ P $ 的坐标为______;
(4) 若在“圆”坐标系中,不在 $ x $ 轴上的点 $ M(x_1,y_1) $ 与点 $ N(x_2,y_2) $ 关于 $ x $ 轴对称,则 $ x_1 $ 与 $ x_2 $、$ y_1 $ 与 $ y_2 $ 分别满足的数量关系是______。
 </题目>
</题目>
<答案>(1)
(2)解:如答图所示,点F和点G即为所求.
∵$OB=OG=3,∠AOB=∠FOG=30^{\circ },OA=OF,$
∴$△AOB\cong △FOG(SAS)$.
(3)
(4)
【问题探究】
(1) 点 $ C $,$ E $ 的坐标分别为______,______;
(2) 在“圆”坐标系内描出点 $ F(6,120^{\circ}) $,$ G(3,150^{\circ}) $,连接 $ AB $,$ FG $,试说明 $ \triangle AOB \cong \triangle FOG $;
(3) 若 $ \triangle OAP $ 是等边三角形,则点 $ P $ 的坐标为______;
(4) 若在“圆”坐标系中,不在 $ x $ 轴上的点 $ M(x_1,y_1) $ 与点 $ N(x_2,y_2) $ 关于 $ x $ 轴对称,则 $ x_1 $ 与 $ x_2 $、$ y_1 $ 与 $ y_2 $ 分别满足的数量关系是______。
 </题目>
</题目><答案>(1)
$(6,90^{\circ })$
$(7,240^{\circ })$
(2)解:如答图所示,点F和点G即为所求.
∵$OB=OG=3,∠AOB=∠FOG=30^{\circ },OA=OF,$
∴$△AOB\cong △FOG(SAS)$.
(3)
$(6,60^{\circ })$或$(6,300^{\circ })$
(4)
$x_{1}=x_{2},y_{1}+y_{2}=360^{\circ }$
答案:
(1)$(6,90^{\circ })$ $(7,240^{\circ })$
(2)解:如答图所示,点F和点G即为所求.

∵$OB=OG=3,∠AOB=∠FOG=30^{\circ },OA=OF,$
∴$△AOB\cong △FOG(SAS)$.
(3)$(6,60^{\circ })$或$(6,300^{\circ })$
(4)$x_{1}=x_{2},y_{1}+y_{2}=360^{\circ }$
(1)$(6,90^{\circ })$ $(7,240^{\circ })$
(2)解:如答图所示,点F和点G即为所求.

∵$OB=OG=3,∠AOB=∠FOG=30^{\circ },OA=OF,$
∴$△AOB\cong △FOG(SAS)$.
(3)$(6,60^{\circ })$或$(6,300^{\circ })$
(4)$x_{1}=x_{2},y_{1}+y_{2}=360^{\circ }$