1. 在平面直角坐标系中,将一条与 $ y $ 轴重合的直线绕原点逆时针旋转 $ 45^{\circ} $,下面四个点中一定会被这条直线扫到的是(
A.$ (3,2) $
B.$ (-2,3) $
C.$ (-2,-3) $
D.$ (3,-2) $
B
)A.$ (3,2) $
B.$ (-2,3) $
C.$ (-2,-3) $
D.$ (3,-2) $
答案：B
解析：
与y轴重合的直线为y轴，绕原点逆时针旋转$45°$后，直线的倾斜角为$90° + 45°=135°$，其斜率$k=\tan 135°=-1$，直线方程为$y=-x$，即$x + y=0$。
A. $3 + 2=5\neq0$，不在直线上；
B. $-2 + 3=1\neq0$，不在直线上；
C. $-2 + (-3)=-5\neq0$，不在直线上；
D. $3 + (-2)=1\neq0$，不在直线上。
1
A. $3 + 2=5\neq0$，不在直线上；
B. $-2 + 3=1\neq0$，不在直线上；
C. $-2 + (-3)=-5\neq0$，不在直线上；
D. $3 + (-2)=1\neq0$，不在直线上。
1
2. 已知点 $ P(5a + 1,6a + 2) $ 在第一、三象限的角平分线上,则 $ a = $
-1
。答案：-1
解析：
因为点$P(5a + 1,6a + 2)$在第一、三象限的角平分线上，所以该点的横纵坐标相等，即$5a + 1 = 6a + 2$。
解方程：$5a + 1 = 6a + 2$
移项可得：$1 - 2 = 6a - 5a$
计算得：$-1 = a$
所以$a = -1$
$-1$
解方程：$5a + 1 = 6a + 2$
移项可得：$1 - 2 = 6a - 5a$
计算得：$-1 = a$
所以$a = -1$
$-1$
3. 如果点 $ P(x,y) $ 的坐标满足 $ x + y = xy $,那么称点 $ P $ 为和谐点。请写出一个和谐点的坐标：
(2,2)
。答案：答案不唯一,如(2,2)或$(-1,\frac {1}{2})$
4. 已知 $ P(2x - 3,3 - x) $,$ Q(3,2) $。若 $ PQ // x $ 轴,则线段 $ PQ $ 的长度为
4
。答案：4
解析：
因为 $PQ // x$ 轴，所以点 $P$ 与点 $Q$ 的纵坐标相等。
点 $Q$ 的纵坐标为 $2$，点 $P$ 的纵坐标为 $3 - x$，则：
$3 - x = 2$
解得 $x = 1$
将 $x = 1$ 代入点 $P$ 的横坐标 $2x - 3$，得：
$2×1 - 3 = -1$
所以点 $P$ 的坐标为 $(-1, 2)$
点 $Q$ 的坐标为 $(3, 2)$，因为 $PQ // x$ 轴，所以线段 $PQ$ 的长度为两点横坐标差的绝对值，即：
$|3 - (-1)| = |4| = 4$
4
点 $Q$ 的纵坐标为 $2$，点 $P$ 的纵坐标为 $3 - x$，则：
$3 - x = 2$
解得 $x = 1$
将 $x = 1$ 代入点 $P$ 的横坐标 $2x - 3$，得：
$2×1 - 3 = -1$
所以点 $P$ 的坐标为 $(-1, 2)$
点 $Q$ 的坐标为 $(3, 2)$，因为 $PQ // x$ 轴，所以线段 $PQ$ 的长度为两点横坐标差的绝对值，即：
$|3 - (-1)| = |4| = 4$
4
5. (2024·齐齐哈尔)如图,在平面直角坐标系中,以点 $ O $ 为圆心,适当长为半径画弧,交 $ x $ 轴正半轴于点 $ M $,交 $ y $ 轴正半轴于点 $ N $,再分别以点 $ M $,$ N $ 为圆心,大于 $ \frac{1}{2}MN $ 的长为半径画弧,两弧在第一象限交于点 $ H $,画射线 $ OH $,若 $ H(2a - 1,a + 1) $,则 $ a = $
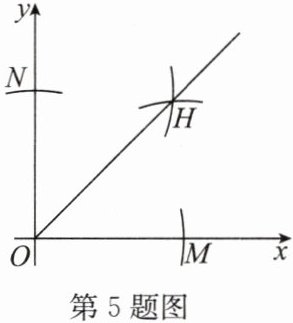
2
。答案：2
解析：
解：由作图可知，射线$OH$是第一象限的角平分线，
因此点$H$的横纵坐标相等，即$2a - 1 = a + 1$，
解得$a = 2$。
$2$
因此点$H$的横纵坐标相等，即$2a - 1 = a + 1$，
解得$a = 2$。
$2$
6. 已知点 $ M(3,-1) $ 与点 $ M'(x,y) $ 在同一条平行于 $ x $ 轴的直线上,且点 $ M' $ 到 $ y $ 轴的距离等于 $ 4 $,那么点 $ M' $ 的坐标是(
A.$ (4,1) $ 或 $ (-4,1) $
B.$ (4,-1) $ 或 $ (-4,-1) $
C.$ (4,-1) $ 或 $ (-5,-1) $
D.$ (4,-1) $ 或 $ (-1,-1) $
B
)A.$ (4,1) $ 或 $ (-4,1) $
B.$ (4,-1) $ 或 $ (-4,-1) $
C.$ (4,-1) $ 或 $ (-5,-1) $
D.$ (4,-1) $ 或 $ (-1,-1) $
答案：B
解析：
因为点$M(3,-1)$与点$M'(x,y)$在同一条平行于$x$轴的直线上，所以点$M'$的纵坐标$y=-1$。
又因为点$M'$到$y$轴的距离等于$4$，所以$|x|=4$，即$x=4$或$x=-4$。
因此，点$M'$的坐标是$(4,-1)$或$(-4,-1)$。
B
又因为点$M'$到$y$轴的距离等于$4$，所以$|x|=4$，即$x=4$或$x=-4$。
因此，点$M'$的坐标是$(4,-1)$或$(-4,-1)$。
B
7. 在平面直角坐标系中,点 $ A $ 的坐标为 $ (-1,-2) $,$ AB $ 平行于 $ y $ 轴,且 $ AB = 5 $,则点 $ B $ 的坐标为(
A.$ (-1,3) $
B.$ (4,-2) $
C.$ (-1,3) $ 或 $ (-1,-7) $
D.$ (4,-2) $ 或 $ (-6,-2) $
C
)A.$ (-1,3) $
B.$ (4,-2) $
C.$ (-1,3) $ 或 $ (-1,-7) $
D.$ (4,-2) $ 或 $ (-6,-2) $
答案：C
解析：
因为AB平行于y轴，点A的坐标为(-1,-2)，所以点B的横坐标与点A相同，为-1。
设点B的坐标为(-1,y)。
因为AB=5，所以|y - (-2)| = 5，即|y + 2| = 5。
当y + 2 = 5时，y = 3；当y + 2 = -5时，y = -7。
所以点B的坐标为(-1,3)或(-1,-7)。
C
设点B的坐标为(-1,y)。
因为AB=5，所以|y - (-2)| = 5，即|y + 2| = 5。
当y + 2 = 5时，y = 3；当y + 2 = -5时，y = -7。
所以点B的坐标为(-1,3)或(-1,-7)。
C
8. 已知平面直角坐标系中的不同点 $ A(3,a - 1) $,$ B(b + 1,-2) $,则下列说法中正确的是(
A.若点 $ A $ 在第一、三象限的角平分线上,则 $ a = 3 $
B.若点 $ B $ 在第二、四象限的角平分线上,则 $ b = -4 $
C.若直线 $ AB $ 平行于 $ x $ 轴,则 $ a = -1 $ 且 $ b \neq 2 $
D.若直线 $ AB $ 平行于 $ y $ 轴,且 $ AB = 3 $,则 $ b = 2 $,$ a = 2 $
C
)A.若点 $ A $ 在第一、三象限的角平分线上,则 $ a = 3 $
B.若点 $ B $ 在第二、四象限的角平分线上,则 $ b = -4 $
C.若直线 $ AB $ 平行于 $ x $ 轴,则 $ a = -1 $ 且 $ b \neq 2 $
D.若直线 $ AB $ 平行于 $ y $ 轴,且 $ AB = 3 $,则 $ b = 2 $,$ a = 2 $
答案：C
解析：
A. 若点$A$在第一、三象限的角平分线上，则$3 = a - 1$，解得$a = 4$，故A错误。
B. 若点$B$在第二、四象限的角平分线上，则$b + 1 = 2$，解得$b = 1$，故B错误。
C. 若直线$AB$平行于$x$轴，则$a - 1 = -2$且$b + 1 \neq 3$，解得$a = -1$且$b \neq 2$，故C正确。
D. 若直线$AB$平行于$y$轴，则$b + 1 = 3$，解得$b = 2$，$AB = |(a - 1) - (-2)| = |a + 1| = 3$，解得$a = 2$或$a = -4$，故D错误。
结论：C
B. 若点$B$在第二、四象限的角平分线上，则$b + 1 = 2$，解得$b = 1$，故B错误。
C. 若直线$AB$平行于$x$轴，则$a - 1 = -2$且$b + 1 \neq 3$，解得$a = -1$且$b \neq 2$，故C正确。
D. 若直线$AB$平行于$y$轴，则$b + 1 = 3$，解得$b = 2$，$AB = |(a - 1) - (-2)| = |a + 1| = 3$，解得$a = 2$或$a = -4$，故D错误。
结论：C
9. (2024·成都)如图,在平面直角坐标系 $ xOy $ 中,已知 $ A(3,0) $,$ B(0,2) $,过点 $ B $ 作 $ y $ 轴的垂线 $ l $,$ P $ 为直线 $ l $ 上一动点,连接 $ PO $,$ PA $,则 $ PO + PA $ 的最小值为
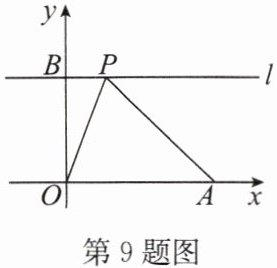
5
。答案：5
解析：
解：作点 $ O $ 关于直线 $ l $ 的对称点 $ O'(0,4) $，连接 $ O'A $ 交直线 $ l $ 于点 $ P $。
直线 $ l $ 为 $ y=2 $，点 $ O(0,0) $ 关于 $ l $ 的对称点 $ O'(0,4) $。
$ A(3,0) $，则 $ O'A = \sqrt{(3-0)^2 + (0-4)^2} = \sqrt{9 + 16} = 5 $。
$ PO + PA = PO' + PA = O'A = 5 $。
5
直线 $ l $ 为 $ y=2 $，点 $ O(0,0) $ 关于 $ l $ 的对称点 $ O'(0,4) $。
$ A(3,0) $，则 $ O'A = \sqrt{(3-0)^2 + (0-4)^2} = \sqrt{9 + 16} = 5 $。
$ PO + PA = PO' + PA = O'A = 5 $。
5