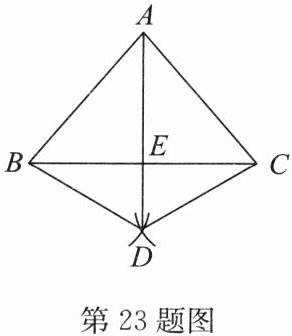
23. (10分)(2024·苏州改编)如图,在$\triangle ABC$中,$AB = AC$,分别以点$B$,$C$为圆心,大于$\frac{1}{2}BC$长为半径画弧,两弧交于点$D$,连接$BD$,$CD$,$AD$,$AD与BC交于点E$.
(1)求证:$\triangle ABD\cong\triangle ACD$;
(2)若$BD = 2$,$\angle BDC = 120^{\circ}$,求$DE$的长.
(1)求证:$\triangle ABD\cong\triangle ACD$;
(2)若$BD = 2$,$\angle BDC = 120^{\circ}$,求$DE$的长.

答案:
(1)证明:由作图知BD=CD.在△ABD和△ACD中,{AB=AC,AD=AD,BD=CD,
∴△ABD≌△ACD(SSS).
(2)解:
∵AB=AC,BD=CD,
∴AD垂直平分BC,即BE=CE.
∵△ABD≌△ACD,
∴∠ADB=∠ADC.
∵∠BDC=120°,
∴∠BDE=60°,∠DBE=30°,
∴DE=$\frac{1}{2}$BD=1.
(1)证明:由作图知BD=CD.在△ABD和△ACD中,{AB=AC,AD=AD,BD=CD,
∴△ABD≌△ACD(SSS).
(2)解:
∵AB=AC,BD=CD,
∴AD垂直平分BC,即BE=CE.
∵△ABD≌△ACD,
∴∠ADB=∠ADC.
∵∠BDC=120°,
∴∠BDE=60°,∠DBE=30°,
∴DE=$\frac{1}{2}$BD=1.
24. (12分)折纸常常能够为证明一个命题提供思路和方法.
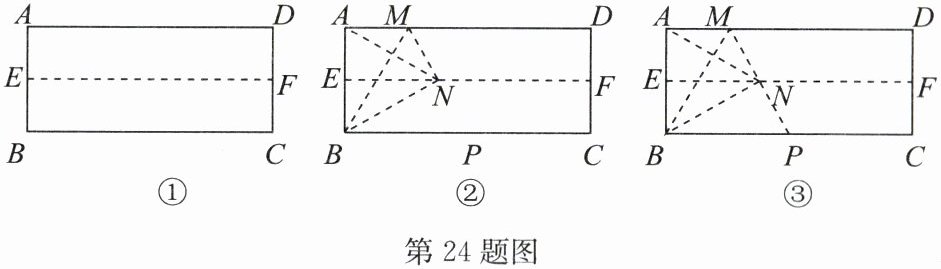
【操作】操作①:对折长方形纸片$ABCD$,使$AD与BC$重合,得到折痕$EF$,把纸片展开(如图①).
操作②:再一次折叠纸片,使点$A落在EF$上,并使折痕经过点$B$,得到折痕$BM$,同时得到线段$BN$,连接$AN$,$MN$(如图②).
【思考】(1)已知点$A$,$B关于直线EF$对称,则$AN与BN$的大小关系是
【探究】(2)若延长$MN交BC于点P$,如图③,试判定$\triangle BMP$的形状,并证明你的结论.
(2)解:△BMP为等边三角形,理由:由
(1)知AB=AN=BN,
∴△ABN为等边三角形,
∴∠ABN=60°.由折叠知∠ABM=∠NBM=30°,∠BAM=∠BNM=90°=∠BNP.
∵∠ABC=90°,
∴∠PBN=30°=∠MBN.又
∵BN=BN,
∴△BNP≌△BNM(ASA),
∴BP=BM.又
∵∠PBM=60°,
∴△BMP为等边三角形.
【操作】操作①:对折长方形纸片$ABCD$,使$AD与BC$重合,得到折痕$EF$,把纸片展开(如图①).
操作②:再一次折叠纸片,使点$A落在EF$上,并使折痕经过点$B$,得到折痕$BM$,同时得到线段$BN$,连接$AN$,$MN$(如图②).
【思考】(1)已知点$A$,$B关于直线EF$对称,则$AN与BN$的大小关系是
相等
;点$A$,$N关于BM$对称,则$AB与BN$的大小关系是相等
.【探究】(2)若延长$MN交BC于点P$,如图③,试判定$\triangle BMP$的形状,并证明你的结论.

(2)解:△BMP为等边三角形,理由:由
(1)知AB=AN=BN,
∴△ABN为等边三角形,
∴∠ABN=60°.由折叠知∠ABM=∠NBM=30°,∠BAM=∠BNM=90°=∠BNP.
∵∠ABC=90°,
∴∠PBN=30°=∠MBN.又
∵BN=BN,
∴△BNP≌△BNM(ASA),
∴BP=BM.又
∵∠PBM=60°,
∴△BMP为等边三角形.
答案:
(1)相等 相等
(2)解:△BMP为等边三角形,理由:由
(1)知AB=AN=BN,
∴△ABN为等边三角形,
∴∠ABN=60°.由折叠知∠ABM=∠NBM=30°,∠BAM=∠BNM=90°=∠BNP.
∵∠ABC=90°,
∴∠PBN=30°=∠MBN.又
∵BN=BN,
∴△BNP≌△BNM(ASA),
∴BP=BM.又
∵∠PBM=60°,
∴△BMP为等边三角形.
(1)相等 相等
(2)解:△BMP为等边三角形,理由:由
(1)知AB=AN=BN,
∴△ABN为等边三角形,
∴∠ABN=60°.由折叠知∠ABM=∠NBM=30°,∠BAM=∠BNM=90°=∠BNP.
∵∠ABC=90°,
∴∠PBN=30°=∠MBN.又
∵BN=BN,
∴△BNP≌△BNM(ASA),
∴BP=BM.又
∵∠PBM=60°,
∴△BMP为等边三角形.