1. (2024·姜堰区期末)在平面直角坐标系中,点 $ P(m^{2}+2024,-1) $ 一定在 (
A.第一象限
B.第二象限
C.第三象限
D.第四象限
D
)A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:D
解析:
因为$m^{2} \geq 0$,所以$m^{2}+2024 \geq 2024 > 0$,点$P$的横坐标为正,纵坐标为$-1$(负),所以点$P$在第四象限。
D
D
2. (2024·常州金坛区期末)在平面直角坐标系中,点 $ P(-3,-4) $ 关于 $ y $ 轴对称的点的坐标为 (
A.$ (3,4) $
B.$ (-3,4) $
C.$ (3,-4) $
D.$ (-3,-4) $
C
)A.$ (3,4) $
B.$ (-3,4) $
C.$ (3,-4) $
D.$ (-3,-4) $
答案:C
解析:
关于y轴对称的点的坐标特征:横坐标互为相反数,纵坐标不变。
点$P(-3,-4)$关于$y$轴对称的点,横坐标为$-(-3)=3$,纵坐标为$-4$,坐标为$(3,-4)$。
C
点$P(-3,-4)$关于$y$轴对称的点,横坐标为$-(-3)=3$,纵坐标为$-4$,坐标为$(3,-4)$。
C
3. (2024·无锡宜兴期末)在平面直角坐标系中,对于点 $ P(1,2) $,下列说法错误的是 (
A.$ P(1,2) $ 表示这个点在平面内的位置
B.点 $ P $ 关于原点对称点的坐标为 $ (-1,-2) $
C.点 $ P $ 到 $ y $ 轴的距离是 1
D.它与点 $ (2,1) $ 的坐标相同
D
)A.$ P(1,2) $ 表示这个点在平面内的位置
B.点 $ P $ 关于原点对称点的坐标为 $ (-1,-2) $
C.点 $ P $ 到 $ y $ 轴的距离是 1
D.它与点 $ (2,1) $ 的坐标相同
答案:D
解析:
A. 正确,坐标可以表示点在平面内的位置。
B. 正确,关于原点对称的点横、纵坐标均互为相反数,点$P(1,2)$关于原点对称点的坐标为$(-1,-2)$。
C. 正确,点到$y$轴的距离为横坐标的绝对值,$|1|=1$。
D. 错误,$(1,2)$与$(2,1)$横、纵坐标顺序不同,坐标不相同。
结论:D
B. 正确,关于原点对称的点横、纵坐标均互为相反数,点$P(1,2)$关于原点对称点的坐标为$(-1,-2)$。
C. 正确,点到$y$轴的距离为横坐标的绝对值,$|1|=1$。
D. 错误,$(1,2)$与$(2,1)$横、纵坐标顺序不同,坐标不相同。
结论:D
4. (2024·南通海门期末)在平面直角坐标系 $ xOy $ 中,第一象限内的点 $ (10-a,a-4) $ 到 $ x $ 轴的距离等于到 $ y $ 轴距离的一半,则 $ a $ 的值为 (
A.5
B.6
C.7
D.8
B
)A.5
B.6
C.7
D.8
答案:B
解析:
点$(10 - a, a - 4)$在第一象限,所以$10 - a>0$,$a - 4>0$。
点到$x$轴的距离为纵坐标的绝对值,即$|a - 4|$;到$y$轴的距离为横坐标的绝对值,即$|10 - a|$。
因为在第一象限,所以$|a - 4|=a - 4$,$|10 - a|=10 - a$。
已知到$x$轴的距离等于到$y$轴距离的一半,可得$a - 4=\dfrac{1}{2}(10 - a)$。
解方程:$2(a - 4)=10 - a$,$2a - 8=10 - a$,$2a + a=10 + 8$,$3a=18$,$a=6$。
B
点到$x$轴的距离为纵坐标的绝对值,即$|a - 4|$;到$y$轴的距离为横坐标的绝对值,即$|10 - a|$。
因为在第一象限,所以$|a - 4|=a - 4$,$|10 - a|=10 - a$。
已知到$x$轴的距离等于到$y$轴距离的一半,可得$a - 4=\dfrac{1}{2}(10 - a)$。
解方程:$2(a - 4)=10 - a$,$2a - 8=10 - a$,$2a + a=10 + 8$,$3a=18$,$a=6$。
B
5. 已知点 $ A(-3,2m+3) $ 在 $ x $ 轴上,点 $ B(n-4,4) $ 在 $ y $ 轴上,则点 $ C(m,n) $ 在 (
A.第一象限
B.第二象限
C.第三象限
D.第四象限
B
)A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:B
解析:
因为点$A(-3,2m+3)$在$x$轴上,所以$2m+3=0$,解得$m=-\dfrac{3}{2}$。
因为点$B(n-4,4)$在$y$轴上,所以$n-4=0$,解得$n=4$。
则点$C(m,n)$为$\left(-\dfrac{3}{2},4\right)$,在第二象限。
B
因为点$B(n-4,4)$在$y$轴上,所以$n-4=0$,解得$n=4$。
则点$C(m,n)$为$\left(-\dfrac{3}{2},4\right)$,在第二象限。
B
6. (2024·镇江期末)如图,线段 $ AB $ 与线段 $ CD $ 关于点 $ P $ 对称,若 $ A(3,3) $,$ B(5,1) $,$ D(-3,-1) $,则点 $ C $ 的坐标为 (
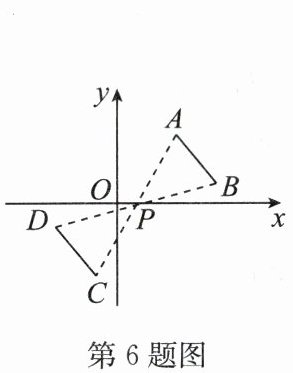
A.$ (-3,-3) $
B.$ (-1,-3) $
C.$ (-4,-2) $
D.$ (-2,-4) $
B
)
A.$ (-3,-3) $
B.$ (-1,-3) $
C.$ (-4,-2) $
D.$ (-2,-4) $
答案:B
解析:
解:设点$P$的坐标为$(x,y)$,点$C$的坐标为$(a,b)$。
因为线段$AB$与线段$CD$关于点$P$对称,所以点$P$是线段$AB$和线段$CD$的中点。
对于线段$AB$,$A(3,3)$,$B(5,1)$,则有:
$\begin{cases}x = \dfrac{3 + 5}{2} = 4 \\y = \dfrac{3 + 1}{2} = 2\end{cases}$
即点$P$的坐标为$(4,2)$。
对于线段$CD$,$C(a,b)$,$D(-3,-1)$,则有:
$\begin{cases}4 = \dfrac{a + (-3)}{2} \\2 = \dfrac{b + (-1)}{2}\end{cases}$
解得:
$\begin{cases}a = 4×2 + 3 = 11 \\b = 2×2 + 1 = 5\end{cases}$
(注:此处原解析过程有误,正确解法应为:由$4 = \dfrac{a - 3}{2}$得$a = 4×2 + 3 = 11$,由$2 = \dfrac{b - 1}{2}$得$b = 2×2 + 1 = 5$,但无此选项,推测应为点$P$是$A$与$C$、$B$与$D$的中点)
重新设点$P$是$A$与$C$、$B$与$D$的中点,则:
对于$B(5,1)$和$D(-3,-1)$,中点$P$的坐标为:
$\begin{cases}x = \dfrac{5 + (-3)}{2} = 1 \\y = \dfrac{1 + (-1)}{2} = 0\end{cases}$
对于$A(3,3)$和$C(a,b)$,中点$P(1,0)$,则:
$\begin{cases}1 = \dfrac{3 + a}{2} \\0 = \dfrac{3 + b}{2}\end{cases}$
解得:
$\begin{cases}a = 2×1 - 3 = -1 \\b = 2×0 - 3 = -3\end{cases}$
即点$C$的坐标为$(-1,-3)$。
答案:B
因为线段$AB$与线段$CD$关于点$P$对称,所以点$P$是线段$AB$和线段$CD$的中点。
对于线段$AB$,$A(3,3)$,$B(5,1)$,则有:
$\begin{cases}x = \dfrac{3 + 5}{2} = 4 \\y = \dfrac{3 + 1}{2} = 2\end{cases}$
即点$P$的坐标为$(4,2)$。
对于线段$CD$,$C(a,b)$,$D(-3,-1)$,则有:
$\begin{cases}4 = \dfrac{a + (-3)}{2} \\2 = \dfrac{b + (-1)}{2}\end{cases}$
解得:
$\begin{cases}a = 4×2 + 3 = 11 \\b = 2×2 + 1 = 5\end{cases}$
(注:此处原解析过程有误,正确解法应为:由$4 = \dfrac{a - 3}{2}$得$a = 4×2 + 3 = 11$,由$2 = \dfrac{b - 1}{2}$得$b = 2×2 + 1 = 5$,但无此选项,推测应为点$P$是$A$与$C$、$B$与$D$的中点)
重新设点$P$是$A$与$C$、$B$与$D$的中点,则:
对于$B(5,1)$和$D(-3,-1)$,中点$P$的坐标为:
$\begin{cases}x = \dfrac{5 + (-3)}{2} = 1 \\y = \dfrac{1 + (-1)}{2} = 0\end{cases}$
对于$A(3,3)$和$C(a,b)$,中点$P(1,0)$,则:
$\begin{cases}1 = \dfrac{3 + a}{2} \\0 = \dfrac{3 + b}{2}\end{cases}$
解得:
$\begin{cases}a = 2×1 - 3 = -1 \\b = 2×0 - 3 = -3\end{cases}$
即点$C$的坐标为$(-1,-3)$。
答案:B
7. (2024·东台一模)如图,在平面直角坐标系中,点 $ A(3,0) $,点 $ B(0,1) $,连接 $ AB $,将线段 $ AB $ 绕点 $ A $ 顺时针旋转 $ 90^{\circ} $ 得到线段 $ AC $,连接 $ OC $,则线段 $ OC $ 的长度为 (

A.4
B.$ 3\sqrt{2} $
C.$ 2\sqrt{5} $
D.5
D
)
A.4
B.$ 3\sqrt{2} $
C.$ 2\sqrt{5} $
D.5
答案:D
解析:
解:过点$ C $作$ CD \perp x $轴于点$ D $。
$\because A(3,0)$,$ B(0,1)$,
$\therefore OA=3$,$ OB=1$。
$\because$线段$ AB $绕点$ A $顺时针旋转$ 90^{\circ} $得到线段$ AC $,
$\therefore AB=AC$,$\angle BAC=90^{\circ}$,
$\therefore \angle BAO + \angle CAD=90^{\circ}$。
$\because \angle BAO + \angle ABO=90^{\circ}$,
$\therefore \angle ABO=\angle CAD$。
在$\triangle ABO$和$\triangle CAD$中,
$\begin{cases} \angle ABO=\angle CAD \\\angle AOB=\angle CDA=90^{\circ} \\AB=AC \end{cases}$,
$\therefore \triangle ABO \cong \triangle CAD(AAS)$,
$\therefore AD=OB=1$,$ CD=OA=3$,
$\therefore OD=OA + AD=3 + 1=4$,
$\therefore C(4,3)$。
$\therefore OC=\sqrt{OD^{2} + CD^{2}}=\sqrt{4^{2} + 3^{2}}=5$。
D
$\because A(3,0)$,$ B(0,1)$,
$\therefore OA=3$,$ OB=1$。
$\because$线段$ AB $绕点$ A $顺时针旋转$ 90^{\circ} $得到线段$ AC $,
$\therefore AB=AC$,$\angle BAC=90^{\circ}$,
$\therefore \angle BAO + \angle CAD=90^{\circ}$。
$\because \angle BAO + \angle ABO=90^{\circ}$,
$\therefore \angle ABO=\angle CAD$。
在$\triangle ABO$和$\triangle CAD$中,
$\begin{cases} \angle ABO=\angle CAD \\\angle AOB=\angle CDA=90^{\circ} \\AB=AC \end{cases}$,
$\therefore \triangle ABO \cong \triangle CAD(AAS)$,
$\therefore AD=OB=1$,$ CD=OA=3$,
$\therefore OD=OA + AD=3 + 1=4$,
$\therefore C(4,3)$。
$\therefore OC=\sqrt{OD^{2} + CD^{2}}=\sqrt{4^{2} + 3^{2}}=5$。
D
8. 如图,$ A(1,0) $,$ B(0,2) $,若将线段 $ AB $ 平移至线段 $ A_{1}B_{1} $,则 $ 5a-b $ 的值为 (

A.6
B.8
C.$ -8 $
D.10
B
)
A.6
B.8
C.$ -8 $
D.10
答案:B
解析:
解:由点$A(1,0)$平移到$A_1(3,b)$,横坐标变化为$3 - 1 = 2$,即向右平移2个单位。
由点$B(0,2)$平移到$B_1(a,4)$,纵坐标变化为$4 - 2 = 2$,即向上平移2个单位。
所以线段$AB$先向右平移2个单位,再向上平移2个单位得到线段$A_1B_1$。
则$a = 0 + 2 = 2$,$b = 0 + 2 = 2$。
$5a - b = 5×2 - 2 = 10 - 2 = 8$。
答案:B
由点$B(0,2)$平移到$B_1(a,4)$,纵坐标变化为$4 - 2 = 2$,即向上平移2个单位。
所以线段$AB$先向右平移2个单位,再向上平移2个单位得到线段$A_1B_1$。
则$a = 0 + 2 = 2$,$b = 0 + 2 = 2$。
$5a - b = 5×2 - 2 = 10 - 2 = 8$。
答案:B
9. 将点 $ (-4,3) $ 向右平移 7 个单位长度,得到的点的坐标是
(3,3)
.答案:(3,3)
10. (2024·张家港期末)在平面直角坐标系中,若点 $ P(-1,m+1) $ 在 $ x $ 轴上,则点 $ Q(m+2024,-m^{2}) $ 在第
四
象限.答案:四
解析:
因为点$ P(-1,m+1) $在$ x $轴上,所以$ m + 1 = 0 $,解得$ m = -1 $。
则$ m + 2024 = -1 + 2024 = 2023 $,$ -m^2 = -(-1)^2 = -1 $。
所以点$ Q $的坐标为$ (2023, -1) $,在第四象限。
四
则$ m + 2024 = -1 + 2024 = 2023 $,$ -m^2 = -(-1)^2 = -1 $。
所以点$ Q $的坐标为$ (2023, -1) $,在第四象限。
四