11. 点 $ M(-1,3) $ 与点 $ N $ 关于 $ x $ 轴对称,则点 $ N $ 的坐标为
(-1,-3)
.答案:(-1,-3)
12. (2024·常州溧阳期末)已知点 $ P(m,4-m) $ 在过点 $ A(2,3) $,且与 $ x $ 轴平行的直线上,则点 $ P $ 的坐标为
(1,3)
.答案:(1,3)
解析:
与$x$轴平行的直线上的点的纵坐标相等,已知该直线过点$A(2,3)$,所以此直线的解析式为$y = 3$。
因为点$P(m,4 - m)$在该直线上,所以点$P$的纵坐标$4 - m = 3$,解得$m = 1$。
则点$P$的横坐标为$m = 1$,纵坐标为$3$,所以点$P$的坐标为$(1,3)$。
$(1,3)$
因为点$P(m,4 - m)$在该直线上,所以点$P$的纵坐标$4 - m = 3$,解得$m = 1$。
则点$P$的横坐标为$m = 1$,纵坐标为$3$,所以点$P$的坐标为$(1,3)$。
$(1,3)$
13. 长方形 $ ABCO $ 位于如图所示的平面直角坐标系中,且点 $ B(8,4) $,点 $ A $,$ C $ 分别在 $ x $ 轴、$ y $ 轴上,若四边形 $ ABFE $ 与四边形 $ CDFE $ 关于直线 $ EF $ 对称,则点 $ E $ 的坐标为
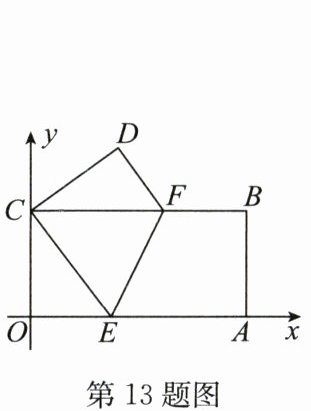
(3,0)
.
答案:(3,0)
解析:
解:
∵四边形$ABCO$是长方形,点$B(8,4)$,
∴$OA=8$,$OC=4$,$A(8,0)$,$C(0,4)$。
设点$E(m,0)$,则$OE=m$,$EA=8 - m$。
∵四边形$ABFE$与四边形$CDFE$关于直线$EF$对称,
∴$CD=AB=4$,$DF=BF$,$CE=AE$。
∵$C(0,4)$,$CD=4$,且$D$在第一象限,
∴$D$点纵坐标为$4 + 4=8$?(此处原解析可能有误,正确思路应为:由对称性质得$CE=AE$,$CE=\sqrt{OE^{2}+OC^{2}}=\sqrt{m^{2}+4^{2}}$,$AE=8 - m$,
∴$\sqrt{m^{2}+16}=8 - m$,
两边平方得$m^{2}+16=(8 - m)^{2}$,
$m^{2}+16=64 - 16m + m^{2}$,
$16m=48$,
$m=3$。
∴点$E$的坐标为$(3,0)$。
$(3,0)$
∵四边形$ABCO$是长方形,点$B(8,4)$,
∴$OA=8$,$OC=4$,$A(8,0)$,$C(0,4)$。
设点$E(m,0)$,则$OE=m$,$EA=8 - m$。
∵四边形$ABFE$与四边形$CDFE$关于直线$EF$对称,
∴$CD=AB=4$,$DF=BF$,$CE=AE$。
∵$C(0,4)$,$CD=4$,且$D$在第一象限,
∴$D$点纵坐标为$4 + 4=8$?(此处原解析可能有误,正确思路应为:由对称性质得$CE=AE$,$CE=\sqrt{OE^{2}+OC^{2}}=\sqrt{m^{2}+4^{2}}$,$AE=8 - m$,
∴$\sqrt{m^{2}+16}=8 - m$,
两边平方得$m^{2}+16=(8 - m)^{2}$,
$m^{2}+16=64 - 16m + m^{2}$,
$16m=48$,
$m=3$。
∴点$E$的坐标为$(3,0)$。
$(3,0)$
14. 在平面直角坐标系中,点 $ A $ 的坐标是 $ (2,-1) $,若 $ AB // y $ 轴,且 $ AB= 9 $,则点 $ B $ 的坐标是
(2,8)或(2,-10)
.答案:(2,8)或(2,-10)
解析:
因为 $ AB // y $ 轴,点 $ A $ 的坐标是 $ (2,-1) $,所以点 $ B $ 的横坐标为 $ 2 $。
设点 $ B $ 的纵坐标为 $ y $,因为 $ AB = 9 $,所以 $ |y - (-1)| = 9 $,即 $ |y + 1| = 9 $。
当 $ y + 1 = 9 $ 时,$ y = 8 $;当 $ y + 1 = -9 $ 时,$ y = -10 $。
所以点 $ B $ 的坐标是 $ (2,8) $ 或 $ (2,-10) $。
设点 $ B $ 的纵坐标为 $ y $,因为 $ AB = 9 $,所以 $ |y - (-1)| = 9 $,即 $ |y + 1| = 9 $。
当 $ y + 1 = 9 $ 时,$ y = 8 $;当 $ y + 1 = -9 $ 时,$ y = -10 $。
所以点 $ B $ 的坐标是 $ (2,8) $ 或 $ (2,-10) $。
15. 如图,在平面直角坐标系中,点 $ B $,$ C $ 在 $ y $ 轴上,$ \triangle ABC $ 是等边三角形,$ AB= 4 $,$ AC $ 与 $ x $ 轴的交点 $ D $ 的坐标是 $ (\sqrt{3},0) $,则点 $ A $ 的坐标为
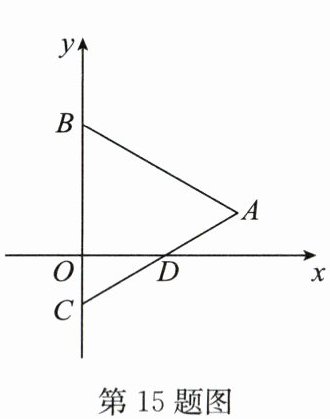
(2√3,1)
.
答案:(2√3,1)
解析:
解:设点$A$的坐标为$(x,y)$,点$C$的坐标为$(0,c)$。
因为$\triangle ABC$是等边三角形,$AB = 4$,所以$AC = 4$。
点$D(\sqrt{3},0)$在$AC$上,设直线$AC$的解析式为$y = kx + c$,将$D(\sqrt{3},0)$代入得$0 = k\sqrt{3} + c$,即$c = -k\sqrt{3}$,所以直线$AC$的解析式为$y = kx - k\sqrt{3}$。
因为点$A(x,y)$在直线$AC$上,所以$y = kx - k\sqrt{3}$。
又因为$AC = 4$,根据两点间距离公式,$\sqrt{(x - 0)^2 + (y - c)^2} = 4$,将$c = -k\sqrt{3}$和$y = kx - k\sqrt{3}$代入得:
$\begin{aligned}\sqrt{x^2 + (kx - k\sqrt{3} + k\sqrt{3})^2} &= 4\\\sqrt{x^2 + (kx)^2} &= 4\\\sqrt{x^2(1 + k^2)} &= 4\\x^2(1 + k^2) &= 16\quad(1)\end{aligned}$
因为点$B$在$y$轴上,设$B(0,b)$,由于$\triangle ABC$是等边三角形,$AB = AC = 4$,且$B$、$C$在$y$轴上,所以$BC$的垂直平分线是$x$轴的平行线,但$A$在第一象限,$D$在$x$轴正半轴,所以$y>0$,$c<0$。
又因为$AD$的长度可表示为$\sqrt{(x - \sqrt{3})^2 + y^2}$,$CD$的长度为$\sqrt{(\sqrt{3} - 0)^2 + (0 - c)^2} = \sqrt{3 + c^2}$,且$AD + CD = AC = 4$。
由直线$AC$的斜率$k = \frac{y - 0}{x - \sqrt{3}} = \frac{y}{x - \sqrt{3}}$,即$y = k(x - \sqrt{3})$,代入$(1)$式:
$x^2\left(1 + \left(\frac{y}{x - \sqrt{3}}\right)^2\right) = 16$
又因为$y = k(x - \sqrt{3})$,且$k = \frac{y}{x - \sqrt{3}}$,结合图形可知直线$AC$的倾斜角较小,$k>0$。
假设$k = \frac{1}{\sqrt{3}}$(尝试常见斜率,因为等边三角形内角$60°$,可能与特殊角有关),则直线$AC$的解析式为$y = \frac{1}{\sqrt{3}}x - \frac{1}{\sqrt{3}} × \sqrt{3} = \frac{1}{\sqrt{3}}x - 1$。
此时$y = \frac{x}{\sqrt{3}} - 1$,代入$(1)$式:
$x^2\left(1 + \left(\frac{1}{\sqrt{3}}\right)^2\right) = x^2\left(1 + \frac{1}{3}\right) = x^2 × \frac{4}{3} = 16$
解得$x^2 = 12$,$x = 2\sqrt{3}$($x>0$),则$y = \frac{2\sqrt{3}}{\sqrt{3}} - 1 = 2 - 1 = 1$。
所以点$A$的坐标为$(2\sqrt{3},1)$。
答案:$(2\sqrt{3},1)$
因为$\triangle ABC$是等边三角形,$AB = 4$,所以$AC = 4$。
点$D(\sqrt{3},0)$在$AC$上,设直线$AC$的解析式为$y = kx + c$,将$D(\sqrt{3},0)$代入得$0 = k\sqrt{3} + c$,即$c = -k\sqrt{3}$,所以直线$AC$的解析式为$y = kx - k\sqrt{3}$。
因为点$A(x,y)$在直线$AC$上,所以$y = kx - k\sqrt{3}$。
又因为$AC = 4$,根据两点间距离公式,$\sqrt{(x - 0)^2 + (y - c)^2} = 4$,将$c = -k\sqrt{3}$和$y = kx - k\sqrt{3}$代入得:
$\begin{aligned}\sqrt{x^2 + (kx - k\sqrt{3} + k\sqrt{3})^2} &= 4\\\sqrt{x^2 + (kx)^2} &= 4\\\sqrt{x^2(1 + k^2)} &= 4\\x^2(1 + k^2) &= 16\quad(1)\end{aligned}$
因为点$B$在$y$轴上,设$B(0,b)$,由于$\triangle ABC$是等边三角形,$AB = AC = 4$,且$B$、$C$在$y$轴上,所以$BC$的垂直平分线是$x$轴的平行线,但$A$在第一象限,$D$在$x$轴正半轴,所以$y>0$,$c<0$。
又因为$AD$的长度可表示为$\sqrt{(x - \sqrt{3})^2 + y^2}$,$CD$的长度为$\sqrt{(\sqrt{3} - 0)^2 + (0 - c)^2} = \sqrt{3 + c^2}$,且$AD + CD = AC = 4$。
由直线$AC$的斜率$k = \frac{y - 0}{x - \sqrt{3}} = \frac{y}{x - \sqrt{3}}$,即$y = k(x - \sqrt{3})$,代入$(1)$式:
$x^2\left(1 + \left(\frac{y}{x - \sqrt{3}}\right)^2\right) = 16$
又因为$y = k(x - \sqrt{3})$,且$k = \frac{y}{x - \sqrt{3}}$,结合图形可知直线$AC$的倾斜角较小,$k>0$。
假设$k = \frac{1}{\sqrt{3}}$(尝试常见斜率,因为等边三角形内角$60°$,可能与特殊角有关),则直线$AC$的解析式为$y = \frac{1}{\sqrt{3}}x - \frac{1}{\sqrt{3}} × \sqrt{3} = \frac{1}{\sqrt{3}}x - 1$。
此时$y = \frac{x}{\sqrt{3}} - 1$,代入$(1)$式:
$x^2\left(1 + \left(\frac{1}{\sqrt{3}}\right)^2\right) = x^2\left(1 + \frac{1}{3}\right) = x^2 × \frac{4}{3} = 16$
解得$x^2 = 12$,$x = 2\sqrt{3}$($x>0$),则$y = \frac{2\sqrt{3}}{\sqrt{3}} - 1 = 2 - 1 = 1$。
所以点$A$的坐标为$(2\sqrt{3},1)$。
答案:$(2\sqrt{3},1)$
16. 如图,在平面直角坐标系中,从点 $ P_{1}(-1,0) $,$ P_{2}(-1,-1) $,$ P_{3}(1,-1) $,$ P_{4}(1,1) $,$ P_{5}(-2,1) $,$ P_{6}(-2,-2) $,…依次扩展下去,则点 $ P_{2023} $ 的坐标是
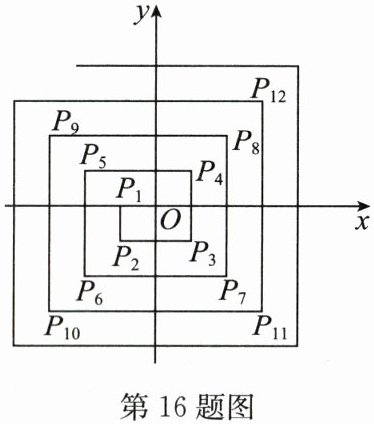
(506,-506)
.
答案:(506,-506)
解析:
解:观察点的坐标规律,每4个点为一组,第$n$组的4个点坐标分别为:
$P_{4k-3}(-k, k-1)$,$P_{4k-2}(-k, -k)$,$P_{4k-1}(k, -k)$,$P_{4k}(k, k)$($k$为正整数)。
因为$2023 = 4×506 - 1$,所以$k = 506$,对应$P_{4k-1}(k, -k)$。
故点$P_{2023}$的坐标是$(506, -506)$。
$(506,-506)$
$P_{4k-3}(-k, k-1)$,$P_{4k-2}(-k, -k)$,$P_{4k-1}(k, -k)$,$P_{4k}(k, k)$($k$为正整数)。
因为$2023 = 4×506 - 1$,所以$k = 506$,对应$P_{4k-1}(k, -k)$。
故点$P_{2023}$的坐标是$(506, -506)$。
$(506,-506)$
17. (8分)如图,方格纸中的每个小方格都是边长为 1 个单位长度的正方形,建立平面直角坐标系后,$ \triangle ABC $ 的顶点均在格点上.
(1)写出点 $ A $,$ B $,$ C $ 的坐标;
(2)写出 $ \triangle ABC $ 关于 $ x $ 轴对称的 $ \triangle A_{1}B_{1}C_{1} $ 的顶点 $ A_{1} $,$ B_{1} $,$ C_{1} $ 的坐标;
(3)求 $ S_{\triangle ABC} $.
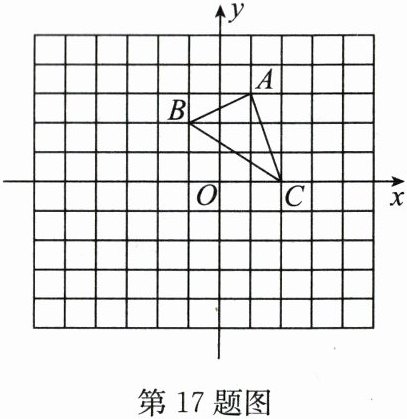
(1)写出点 $ A $,$ B $,$ C $ 的坐标;
(2)写出 $ \triangle ABC $ 关于 $ x $ 轴对称的 $ \triangle A_{1}B_{1}C_{1} $ 的顶点 $ A_{1} $,$ B_{1} $,$ C_{1} $ 的坐标;
(3)求 $ S_{\triangle ABC} $.

答案:解:
(1)A(1,3),B(-1,2),C(2,0).
(2)A₁(1,-3),B₁(-1,-2),C₁(2,0).
(3)S△ABC=3×3-1/2×2×3-1/2×1×3-1/2×2×1=7/2.
(1)A(1,3),B(-1,2),C(2,0).
(2)A₁(1,-3),B₁(-1,-2),C₁(2,0).
(3)S△ABC=3×3-1/2×2×3-1/2×1×3-1/2×2×1=7/2.