21. (8分)正方形 $ ABCD $ 在平面直角坐标系中的位置如图所示,已知点 $ A $ 的坐标为 $ (0,4) $,点 $ D $ 的坐标为 $ (-3,0) $,求 $ B $,$ C $ 两点的坐标.


答案:
解:如答图,过点B作BE⊥y轴于点E,过点C作CF⊥BE于点F,交x轴于点G,则∠AOD=∠BEA=∠CFB=∠DGC=90°.
∵点A的坐标为(0,4),点D的坐标为(-3,0),
∴OA=4,OD=3.
∵四边形ABCD是正方形,
∴AB=BC=CD=DA.
∵∠ADO+∠DAO=∠DAO+∠BAE=90°,
∴∠ADO=∠BAE;同理,∠ADO=∠CBF=∠DCG,
∴△AOD≌△BEA≌△CFB≌△DGC,
∴AO=BE=CF=DG=4,AE=BF=CG=DO=3,
∴OE=EF=FG=GO=1,
∴CG=CF-GF=4-1=3.又
∵点B在第一象限,点C在第四象限,
∴B(4,1),C(1,-3).
解:如答图,过点B作BE⊥y轴于点E,过点C作CF⊥BE于点F,交x轴于点G,则∠AOD=∠BEA=∠CFB=∠DGC=90°.

∵点A的坐标为(0,4),点D的坐标为(-3,0),
∴OA=4,OD=3.
∵四边形ABCD是正方形,
∴AB=BC=CD=DA.
∵∠ADO+∠DAO=∠DAO+∠BAE=90°,
∴∠ADO=∠BAE;同理,∠ADO=∠CBF=∠DCG,
∴△AOD≌△BEA≌△CFB≌△DGC,
∴AO=BE=CF=DG=4,AE=BF=CG=DO=3,
∴OE=EF=FG=GO=1,
∴CG=CF-GF=4-1=3.又
∵点B在第一象限,点C在第四象限,
∴B(4,1),C(1,-3).
22. (10分)如图,点 $ P(3m-1,-2m+4) $ 在第一象限的角平分线 $ OC $ 上,$ AP \perp BP $,点 $ A $ 在 $ x $ 轴正半轴上,点 $ B $ 在 $ y $ 轴正半轴上.
(1)求点 $ P $ 的坐标.
(2)当 $ \angle APB $ 绕点 $ P $ 旋转时,
① $ OA+OB $ 的值是否发生变化?若变化,求出其变化范围;若不变,求出这个定值.
② 请求出 $ OA^{2}+OB^{2} $ 的最小值.

(1)求点 $ P $ 的坐标.
(2)当 $ \angle APB $ 绕点 $ P $ 旋转时,
① $ OA+OB $ 的值是否发生变化?若变化,求出其变化范围;若不变,求出这个定值.
② 请求出 $ OA^{2}+OB^{2} $ 的最小值.

答案:
解:
(1)
∵点P(3m-1,-2m+4)在第一象限的角平分线OC上,
∴3m-1=-2m+4,
∴m=1.
∴点P的坐标为(2,2).
(2)①不变.如答图,过点P作PM⊥y轴于点M,PN⊥x轴于点N,则∠PMO=∠PNO=∠MON=90°. 又
又
∵OC平分∠AOB,
∴PM=PN,
∴四边形OMPN是正方形.
∴∠MPN=∠AOB=90°,OM=ON;
∴∠MPB=∠NPA.
∴△PMB≌△PNA(ASA).
∴NA=BM,PA=PB.
∴OA+OB=ON+AN+OM-BM=2OM=4.
∴当∠APB绕点P旋转时,OA+OB的值为4. ②在Rt△AOB中,OA²+OB²=AB²,在Rt△APB中,AB²=PA²+PB²=2PA²,
∴OA²+OB²=2PA². 当PA最小时,OA²+OB²的值最小,由垂线段最短,知PA的最小值为2,
∴OA²+OB²的最小值为8.
解:
(1)
∵点P(3m-1,-2m+4)在第一象限的角平分线OC上,
∴3m-1=-2m+4,
∴m=1.
∴点P的坐标为(2,2).
(2)①不变.如答图,过点P作PM⊥y轴于点M,PN⊥x轴于点N,则∠PMO=∠PNO=∠MON=90°.
 又
又∵OC平分∠AOB,
∴PM=PN,
∴四边形OMPN是正方形.
∴∠MPN=∠AOB=90°,OM=ON;
∴∠MPB=∠NPA.
∴△PMB≌△PNA(ASA).
∴NA=BM,PA=PB.
∴OA+OB=ON+AN+OM-BM=2OM=4.
∴当∠APB绕点P旋转时,OA+OB的值为4. ②在Rt△AOB中,OA²+OB²=AB²,在Rt△APB中,AB²=PA²+PB²=2PA²,
∴OA²+OB²=2PA². 当PA最小时,OA²+OB²的值最小,由垂线段最短,知PA的最小值为2,
∴OA²+OB²的最小值为8.
23. (10分)如图,正方形 $ OABC $ 的边长为 4,边 $ OA $,$ OC $ 分别在 $ x $ 轴、$ y $ 轴上.
(1)把正方形 $ OABC $ 先向右平移 2 个单位长度,再向上平移 1 个单位长度,得到正方形 $ O'A'B'C' $,在图中画出正方形 $ O'A'B'C' $,并写出点 $ B $ 的对应点 $ B' $ 的坐标;
(2)规定:若 $ a $,$ b $ 为整数,则点 $ (a,b) $ 称为整点,如点 $ (0,4) $ 为整点.求正方形 $ OABC $ 与正方形 $ O'A'B'C' $ 重叠区域(包括边界)内的整点个数;
(3)若点 $ P $ 在 $ x $ 轴上方,以 $ O $,$ A $,$ P $ 为顶点的三角形是以 $ OA $ 为腰的等腰三角形,且 $ \triangle OAP $ 的面积为 2,请求出所有符合条件的点 $ P $ 的坐标.
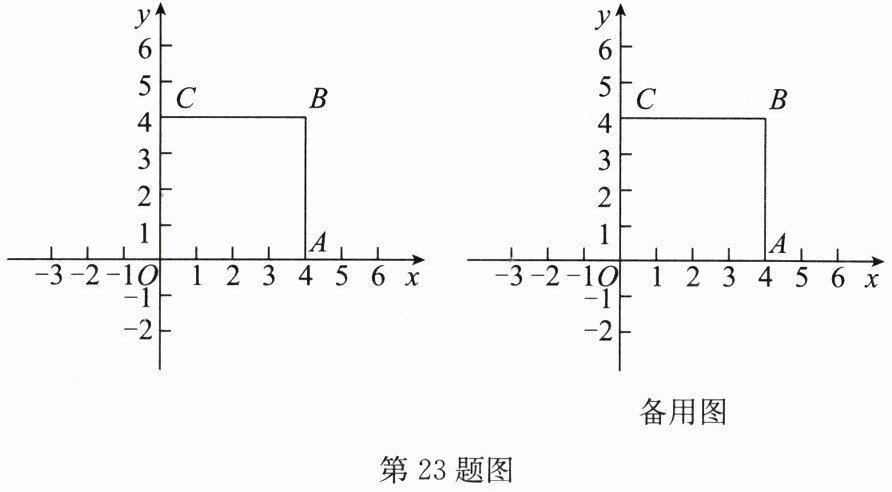
(1)把正方形 $ OABC $ 先向右平移 2 个单位长度,再向上平移 1 个单位长度,得到正方形 $ O'A'B'C' $,在图中画出正方形 $ O'A'B'C' $,并写出点 $ B $ 的对应点 $ B' $ 的坐标;
(2)规定:若 $ a $,$ b $ 为整数,则点 $ (a,b) $ 称为整点,如点 $ (0,4) $ 为整点.求正方形 $ OABC $ 与正方形 $ O'A'B'C' $ 重叠区域(包括边界)内的整点个数;
(3)若点 $ P $ 在 $ x $ 轴上方,以 $ O $,$ A $,$ P $ 为顶点的三角形是以 $ OA $ 为腰的等腰三角形,且 $ \triangle OAP $ 的面积为 2,请求出所有符合条件的点 $ P $ 的坐标.

答案:
解:
(1)如答图,正方形O'A'B'C'即为所求,点B'的坐标为(6,5).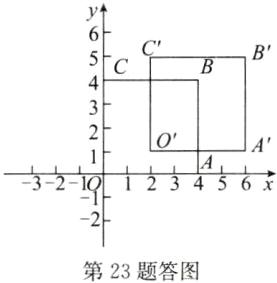
(2)正方形OABC与正方形O'A'B'C'重叠区域(包括边界)内的整点有(2,1),(3,1),(4,1),(2,2),(3,2),(4,2),(2,3),(3,3),(4,3),(2,4),(3,4),(4,4),
∴正方形OABC与正方形O'A'B'C'重叠区域(包括边界)内的整点有12个.
(3)设点P的坐标为(m,n),
∵点P在x轴上方,
∴n>0.由题意知OA=4.
∵△OAP的面积为2,
∴1/2 OA·n=2,即1/2×4·n=2,解得n=1. 当OA=OP=4时,有m²+1²=4²,
∴m=±√15.
∴点P的坐标为(√15,1)或(-√15,1). 当OA=PA=4时,(m-4)²+1²=4²,
∴m=4±√15.
∴点P的坐标为(4+√15,1)或(4-√15,1). 综上所述,点P的坐标为(√15,1)或(-√15,1)或(4+√15,1)或(4-√15,1).
解:
(1)如答图,正方形O'A'B'C'即为所求,点B'的坐标为(6,5).

(2)正方形OABC与正方形O'A'B'C'重叠区域(包括边界)内的整点有(2,1),(3,1),(4,1),(2,2),(3,2),(4,2),(2,3),(3,3),(4,3),(2,4),(3,4),(4,4),
∴正方形OABC与正方形O'A'B'C'重叠区域(包括边界)内的整点有12个.
(3)设点P的坐标为(m,n),
∵点P在x轴上方,
∴n>0.由题意知OA=4.
∵△OAP的面积为2,
∴1/2 OA·n=2,即1/2×4·n=2,解得n=1. 当OA=OP=4时,有m²+1²=4²,
∴m=±√15.
∴点P的坐标为(√15,1)或(-√15,1). 当OA=PA=4时,(m-4)²+1²=4²,
∴m=4±√15.
∴点P的坐标为(4+√15,1)或(4-√15,1). 综上所述,点P的坐标为(√15,1)或(-√15,1)或(4+√15,1)或(4-√15,1).