8. (2024·威海)同一条公路连接A,B,C三地,B地在A,C两地之间. 甲、乙两车分别从A地、B地同时出发前往C地. 甲车的速度始终保持不变,乙车中途休息一段时间,继续行驶. 如图表示甲、乙两车之间的距离$ y \mathrm { km } 与时间 x \mathrm { h } $的函数关系. 下列结论正确的是(
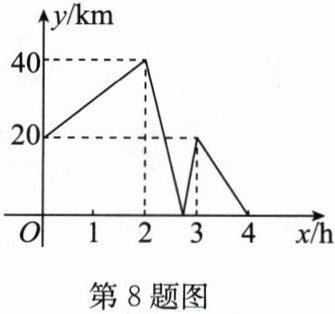
A.甲车行驶$ \frac { 8 } { 3 } \mathrm { h } $与乙车相遇
B.A,C两地相距220km
C.甲车的速度是70km/h
D.乙车中途休息36分钟
A
)
A.甲车行驶$ \frac { 8 } { 3 } \mathrm { h } $与乙车相遇
B.A,C两地相距220km
C.甲车的速度是70km/h
D.乙车中途休息36分钟
答案:A
9. 圆周长C与圆的半径r之间的函数关系式为$ C = 2 \pi r $,其中常量是
2π
.答案:2π
10. 当$ x = - 5 $时,函数$ y = x ^ { 2 } - 5 x $的值为
50
.答案:50
解析:
当$x = -5$时,$y=(-5)^{2}-5×(-5)=25 + 25=50$。
50
50
11. 若一次函数$ y = k x + b 的图象与直线 y = - 3 x $平行,且过点$ ( 1, 2 ) $,则$ k + b = $
2
.答案:2
解析:
因为一次函数$y = kx + b$的图象与直线$y=-3x$平行,所以$k=-3$。
又因为函数过点$(1,2)$,将$x=1$,$y=2$,$k=-3$代入$y = kx + b$,得$2=-3×1 + b$,解得$b=5$。
所以$k + b=-3 + 5=2$。
2
又因为函数过点$(1,2)$,将$x=1$,$y=2$,$k=-3$代入$y = kx + b$,得$2=-3×1 + b$,解得$b=5$。
所以$k + b=-3 + 5=2$。
2
12. 已知点$ A ( x _ { 1 }, y _ { 1 } ) $,$ B ( x _ { 2 }, y _ { 2 } ) 在直线 y = k x + b $上,且直线经过第一、三、四象限,当$ x _ { 1 } < x _ { 2 } $时,$ y _ { 1 } 与 y _ { 2 } $的大小关系为
y₁<y₂
.答案:y₁<y₂
解析:
因为直线$y = kx + b$经过第一、三、四象限,所以$k>0$,$b<0$。
由于$k>0$,所以$y$随$x$的增大而增大。
又因为$x_1 < x_2$,所以$y_1 < y_2$。
$y_1 < y_2$
由于$k>0$,所以$y$随$x$的增大而增大。
又因为$x_1 < x_2$,所以$y_1 < y_2$。
$y_1 < y_2$
13. 在某次登山过程中,海拔每升高1千米,气温平均下降$ 6 ^ { \circ } \mathrm { C } $,已知某登山大本营所在位置的气温是$ 2 ^ { \circ } \mathrm { C } $,登山队员从大本营出发登山,当海拔升高x千米时,所在位置的气温是$ y ^ { \circ } \mathrm { C } $,那么y关于x的函数表达式是
y=-6x+2
.答案:y=-6x+2
14. 一次函数$ y = 2 x + b 的图象过点 ( 0, - 2 ) $,将一次函数$ y = 2 x + b $的图象向下平移5个单位长度,所得图象的函数表达式为
y=2x-7
.答案:y=2x-7
解析:
因为一次函数$y = 2x + b$的图象过点$(0, - 2)$,所以将$x = 0$,$y=-2$代入$y = 2x + b$,得$-2=2×0 + b$,解得$b=-2$,则原函数表达式为$y = 2x-2$。
将函数$y = 2x-2$的图象向下平移$5$个单位长度,根据函数图象平移规律“上加下减”,所得图象的函数表达式为$y=2x-2 - 5=2x-7$。
$y=2x-7$
将函数$y = 2x-2$的图象向下平移$5$个单位长度,根据函数图象平移规律“上加下减”,所得图象的函数表达式为$y=2x-2 - 5=2x-7$。
$y=2x-7$
15. 若点$ A ( a, b ) 在一次函数 y = - 2 x + 3 $的图象上,则$ 4 a ^ { 2 } + b ( 4 a + b ) $的值为
9
.答案:9
解析:
因为点$A(a,b)$在一次函数$y = - 2x + 3$的图象上,所以$b=-2a + 3$,即$2a + b=3$。
$4a^{2}+b(4a + b)=4a^{2}+4ab + b^{2}=(2a + b)^{2}$。
将$2a + b=3$代入上式,得$(2a + b)^{2}=3^{2}=9$。
9
$4a^{2}+b(4a + b)=4a^{2}+4ab + b^{2}=(2a + b)^{2}$。
将$2a + b=3$代入上式,得$(2a + b)^{2}=3^{2}=9$。
9
16. 如图,光源$ A ( - 3, 2 ) $发出的一束光,遇到平面镜(y轴)上的点B反射得到的光线BC交x轴于点$ C ( - 1, 0 ) $,再被平面镜(x轴)上的点C反射得到光线CD,则直线CD的函数表达式为
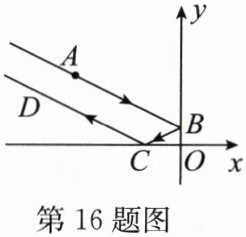
y=−$\frac{1}{2}$x−$\frac{1}{2}$
.
答案:y=−$\frac{1}{2}$x−$\frac{1}{2}$
解析:
解:设点$A(-3,2)$关于$y$轴的对称点为$A'(3,2)$。
因为光线$AB$经$y$轴反射后得到$BC$,所以点$A'$、$B$、$C$三点共线。
设直线$A'C$的函数表达式为$y=kx+b$,将$A'(3,2)$、$C(-1,0)$代入得:
$\begin{cases}3k + b = 2 \\ -k + b = 0\end{cases}$
解得$k = \frac{1}{2}$,$b = \frac{1}{2}$,所以直线$A'C$的表达式为$y = \frac{1}{2}x + \frac{1}{2}$。
令$x = 0$,得$y = \frac{1}{2}$,所以点$B$的坐标为$(0,\frac{1}{2})$。
设点$B(0,\frac{1}{2})$关于$x$轴的对称点为$B'(0,-\frac{1}{2})$。
因为光线$BC$经$x$轴反射后得到$CD$,所以点$B'$、$C$、$D$三点共线。
设直线$CD$的函数表达式为$y = mx + n$,将$B'(0,-\frac{1}{2})$、$C(-1,0)$代入得:
$\begin{cases} -m + n = 0 \\n = -\frac{1}{2}\end{cases}$
解得$m = -\frac{1}{2}$,$n = -\frac{1}{2}$,所以直线$CD$的函数表达式为$y = -\frac{1}{2}x - \frac{1}{2}$。
$y=-\frac{1}{2}x-\frac{1}{2}$
因为光线$AB$经$y$轴反射后得到$BC$,所以点$A'$、$B$、$C$三点共线。
设直线$A'C$的函数表达式为$y=kx+b$,将$A'(3,2)$、$C(-1,0)$代入得:
$\begin{cases}3k + b = 2 \\ -k + b = 0\end{cases}$
解得$k = \frac{1}{2}$,$b = \frac{1}{2}$,所以直线$A'C$的表达式为$y = \frac{1}{2}x + \frac{1}{2}$。
令$x = 0$,得$y = \frac{1}{2}$,所以点$B$的坐标为$(0,\frac{1}{2})$。
设点$B(0,\frac{1}{2})$关于$x$轴的对称点为$B'(0,-\frac{1}{2})$。
因为光线$BC$经$x$轴反射后得到$CD$,所以点$B'$、$C$、$D$三点共线。
设直线$CD$的函数表达式为$y = mx + n$,将$B'(0,-\frac{1}{2})$、$C(-1,0)$代入得:
$\begin{cases} -m + n = 0 \\n = -\frac{1}{2}\end{cases}$
解得$m = -\frac{1}{2}$,$n = -\frac{1}{2}$,所以直线$CD$的函数表达式为$y = -\frac{1}{2}x - \frac{1}{2}$。
$y=-\frac{1}{2}x-\frac{1}{2}$
17. (6分)已知$ y + 2 与 x + 1 $成正比,且$ x = 2 $时,$ y = 7 $. 求y与x之间的函数关系式.
答案:解:
∵y+2与x+1成正比,
∴设y+2=k(x+1).
∵x=2时,y=7,
∴7+2=k(2+1),
∴k=3,
∴y+2=3(x+1),
∴y=3x+1即为所求.
∵y+2与x+1成正比,
∴设y+2=k(x+1).
∵x=2时,y=7,
∴7+2=k(2+1),
∴k=3,
∴y+2=3(x+1),
∴y=3x+1即为所求.
18. (8分)已知一次函数$ y = 3 x - 3 $,在如图所示的网格图中画出它的图象,并根据图象直接回答下列问题:
(1)它的图象与x轴的交点A的坐标是______,与y轴的交点B的坐标是______;
(2)点$ P ( 2, 3 ) $______这个一次函数的图象上;(填“在”或“不在”)
(3)当______时,函数值大于零.
(1)它的图象与x轴的交点A的坐标是______,与y轴的交点B的坐标是______;
(2)点$ P ( 2, 3 ) $______这个一次函数的图象上;(填“在”或“不在”)
(3)当______时,函数值大于零.

答案:
函数y=3x−3的图象如答图所示.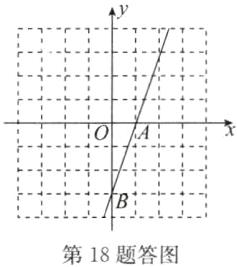
(1)(1,0) (0,−3)
(2)在
(3)x>1
函数y=3x−3的图象如答图所示.

(1)(1,0) (0,−3)
(2)在
(3)x>1