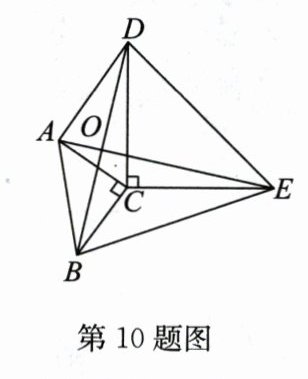
10. 如图,$\triangle ABC和\triangle DCE$都是等腰直角三角形.若$\angle ACB= \angle DCE = 90^{\circ}$,$AC = 2$,$CE = 3$,则$AD^2 + BE^2=$
26
.
答案:26
解析:
连接BD,AE。
因为△ABC和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,
所以AC=BC=2,CD=CE=3,∠ACB=∠DCE=90°。
所以∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE。
在△ACD和△BCE中,
AC=BC,∠ACD=∠BCE,CD=CE,
所以△ACD≌△BCE(SAS),
所以AD=BE。
在Rt△ABC中,AB²=AC²+BC²=2²+2²=8。
在Rt△DCE中,DE²=CD²+CE²=3²+3²=18。
因为∠ABC=∠CDE=45°,
所以∠ABD+∠BDE=∠ABC+∠CBD+∠CDE-∠CDB=45°+∠CBD+45°-∠CDB。
又因为△ACD≌△BCE,所以∠ADC=∠BEC,
所以∠CDB=∠CEB,
所以∠ABD+∠BDE=90°+∠CBD-∠CEB。
因为∠CBD+∠BCD=∠CEB,
所以∠ABD+∠BDE=90°+∠BCD=90°+90°=180°,
所以AB//DE。
过点A作AF⊥DE交ED的延长线于点F,过点B作BG⊥DE于点G,
则四边形AFGB是矩形,所以AF=BG,FG=AB。
设DG=x,EG=y,则DE=x+y=√18=3√2,FG=AB=√8=2√2。
所以DF=FG-DG=2√2 - x,EF=EG+FG=y + 2√2。
在Rt△ADF中,AD²=AF² + DF²=AF² + (2√2 - x)²。
在Rt△BEG中,BE²=BG² + EG²=AF² + y²=AF² + y²。
所以AD² + BE²=2AF² + (2√2 - x)² + y²。
在Rt△BDG中,BG² + DG²=BD²,即AF² + x²=BD²。
在Rt△BDE中,BD² + BE²=DE² + BG² + EG²,(此步推导有误,正确应为利用AB//DE,AF=BG,将AD² + BE²转化为AB² + DE²)
正确方法:因为AB//DE,且AF=BG,
所以AD² + BE²=AF² + DF² + BG² + EG²=2AF² + (2√2 - x)² + y²。
又因为DF + EG=DE - FG=3√2 - 2√2=√2,即(2√2 - x) + y=√2,所以y=x - √2。
因为x + y=3√2,所以x + x - √2=3√2,解得x=2√2,y=√2。
所以DF=2√2 - 2√2=0,即点F与点D重合,
所以AD²=AF²=AC² + CD²=2² + 3²=13,
所以AD² + BE²=2AD²=2×13=26。
26
因为△ABC和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,
所以AC=BC=2,CD=CE=3,∠ACB=∠DCE=90°。
所以∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE。
在△ACD和△BCE中,
AC=BC,∠ACD=∠BCE,CD=CE,
所以△ACD≌△BCE(SAS),
所以AD=BE。
在Rt△ABC中,AB²=AC²+BC²=2²+2²=8。
在Rt△DCE中,DE²=CD²+CE²=3²+3²=18。
因为∠ABC=∠CDE=45°,
所以∠ABD+∠BDE=∠ABC+∠CBD+∠CDE-∠CDB=45°+∠CBD+45°-∠CDB。
又因为△ACD≌△BCE,所以∠ADC=∠BEC,
所以∠CDB=∠CEB,
所以∠ABD+∠BDE=90°+∠CBD-∠CEB。
因为∠CBD+∠BCD=∠CEB,
所以∠ABD+∠BDE=90°+∠BCD=90°+90°=180°,
所以AB//DE。
过点A作AF⊥DE交ED的延长线于点F,过点B作BG⊥DE于点G,
则四边形AFGB是矩形,所以AF=BG,FG=AB。
设DG=x,EG=y,则DE=x+y=√18=3√2,FG=AB=√8=2√2。
所以DF=FG-DG=2√2 - x,EF=EG+FG=y + 2√2。
在Rt△ADF中,AD²=AF² + DF²=AF² + (2√2 - x)²。
在Rt△BEG中,BE²=BG² + EG²=AF² + y²=AF² + y²。
所以AD² + BE²=2AF² + (2√2 - x)² + y²。
在Rt△BDG中,BG² + DG²=BD²,即AF² + x²=BD²。
在Rt△BDE中,BD² + BE²=DE² + BG² + EG²,(此步推导有误,正确应为利用AB//DE,AF=BG,将AD² + BE²转化为AB² + DE²)
正确方法:因为AB//DE,且AF=BG,
所以AD² + BE²=AF² + DF² + BG² + EG²=2AF² + (2√2 - x)² + y²。
又因为DF + EG=DE - FG=3√2 - 2√2=√2,即(2√2 - x) + y=√2,所以y=x - √2。
因为x + y=3√2,所以x + x - √2=3√2,解得x=2√2,y=√2。
所以DF=2√2 - 2√2=0,即点F与点D重合,
所以AD²=AF²=AC² + CD²=2² + 3²=13,
所以AD² + BE²=2AD²=2×13=26。
26
11. (12分)(1)计算:$(\frac{1}{3})^{-2}+(\pi - 2023)^0-\vert2 - \sqrt{9}\vert+\sqrt[3]{-27}$;
(2)求$x$的值:$(2x - 3)^2 - 25 = 0$.
(2)求$x$的值:$(2x - 3)^2 - 25 = 0$.
答案:
(1)6
(2)x=4或x=-1
(1)6
(2)x=4或x=-1
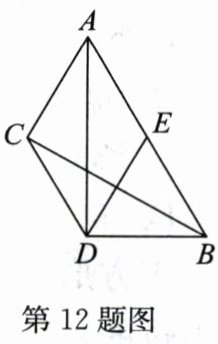
12. (10分)如图,在$\triangle ABC$中,$AD平分\angle BAC$,过点$B作AD$的垂线,垂足为$D$,作$DE// AC$,交$AB于点E$,连接$CD$,$CD// AB$.
(1)求证:$\triangle BDE$是等腰三角形;
(2)求证:$CD = BE$.
(1)求证:$\triangle BDE$是等腰三角形;
(2)求证:$CD = BE$.

答案:
证明:
(1)如答图,
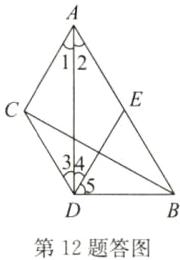
∵DE//AC,
∴∠1=∠4,
∵AD平分∠BAC,
∴∠1=∠2,
∴∠2=∠4.
∵AD⊥BD,
∴∠2+∠ABD=90°,∠5+∠4=90°,
∴∠5=∠ABD,
∴DE=BE,
∴△BDE是等腰三角形.
(2)由
(1)知,∠1=∠2、∠2=∠4.
∵CD//AB,
∴∠2=∠3,
∴∠3=∠4.
又
∵AD=AD,
∴△ACD≌△AED(ASA),
∴CD=DE,由
(1)知DE=BE,
∴CD=BE.
证明:
(1)如答图,

∵DE//AC,
∴∠1=∠4,
∵AD平分∠BAC,
∴∠1=∠2,
∴∠2=∠4.
∵AD⊥BD,
∴∠2+∠ABD=90°,∠5+∠4=90°,
∴∠5=∠ABD,
∴DE=BE,
∴△BDE是等腰三角形.
(2)由
(1)知,∠1=∠2、∠2=∠4.
∵CD//AB,
∴∠2=∠3,
∴∠3=∠4.
又
∵AD=AD,
∴△ACD≌△AED(ASA),
∴CD=DE,由
(1)知DE=BE,
∴CD=BE.
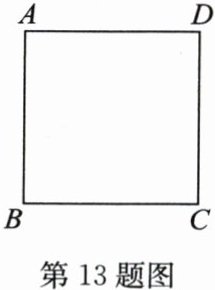
13. (18分)将如图所示的正方形$ABCD$放入平面直角坐标系中,点$A$,$B$,$D的坐标分别为(a,b)$,$(-3,-1)$,$(-a,b)$.
(1)填空:$a = $______,$AB = $______;
(2)画图:在图中画出平面直角坐标系,分别标出$x$轴、$y轴和原点O$,并在顶点$C处标出C$点的坐标;
(3)求对角线$AC$所在直线的函数表达式.
(1)填空:$a = $______,$AB = $______;
(2)画图:在图中画出平面直角坐标系,分别标出$x$轴、$y轴和原点O$,并在顶点$C处标出C$点的坐标;
(3)求对角线$AC$所在直线的函数表达式.

答案:
(1)-3 6
(2)解:如答图所示.
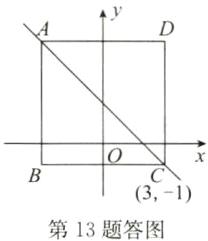
(3)解:设对角线AC所在直线的函数表达式为y=kx+b,将(-3,5)和(3,-1)代入,得
{-3k+b=5,
3k+b=-1,
解得{k=-1,
b=2.
∴对角线AC所在直线的函数表达式为y=-x+2.
(1)-3 6
(2)解:如答图所示.

(3)解:设对角线AC所在直线的函数表达式为y=kx+b,将(-3,5)和(3,-1)代入,得
{-3k+b=5,
3k+b=-1,
解得{k=-1,
b=2.
∴对角线AC所在直线的函数表达式为y=-x+2.