1. 到$\triangle ABC三边距离相等的点是\triangle ABC$的(
A.三条中线的交点
B.三边垂直平分线的交点
C.三条高的交点
D.三条角平分线的交点
D
)A.三条中线的交点
B.三边垂直平分线的交点
C.三条高的交点
D.三条角平分线的交点
答案:D
2. 在等腰三角形$ABC$中,$\angle A = 80^{\circ}$,则$\angle B = $(
A.$20^{\circ}$
B.$50^{\circ}$
C.$80^{\circ}$
D.$80^{\circ}或50^{\circ}或20^{\circ}$
D
)A.$20^{\circ}$
B.$50^{\circ}$
C.$80^{\circ}$
D.$80^{\circ}或50^{\circ}或20^{\circ}$
答案:D
解析:
情况1:若∠A为顶角,则∠B=∠C,∠B=(180°-80°)/2=50°
情况2:若∠A为底角,∠B为顶角,则∠B=180°-2×80°=20°
情况3:若∠A为底角,∠B为底角,则∠B=∠A=80°
∠B=80°或50°或20°
D
情况2:若∠A为底角,∠B为顶角,则∠B=180°-2×80°=20°
情况3:若∠A为底角,∠B为底角,则∠B=∠A=80°
∠B=80°或50°或20°
D
3. 下列各组数中,以它们为边长的线段能构成直角三角形的是(
A.$5,12,13$
B.$1,\sqrt{2},3$
C.$\sqrt{3},\sqrt{4},\sqrt{5}$
D.$1,3,4$
A
)A.$5,12,13$
B.$1,\sqrt{2},3$
C.$\sqrt{3},\sqrt{4},\sqrt{5}$
D.$1,3,4$
答案:A
解析:
A选项:$5^2 + 12^2 = 25 + 144 = 169 = 13^2$,能构成直角三角形。
B选项:$1^2 + (\sqrt{2})^2 = 1 + 2 = 3 \neq 3^2$,不能构成直角三角形。
C选项:$(\sqrt{3})^2 + (\sqrt{4})^2 = 3 + 4 = 7 \neq (\sqrt{5})^2$,不能构成直角三角形。
D选项:$1^2 + 3^2 = 1 + 9 = 10 \neq 4^2$,不能构成直角三角形。
结论:A
B选项:$1^2 + (\sqrt{2})^2 = 1 + 2 = 3 \neq 3^2$,不能构成直角三角形。
C选项:$(\sqrt{3})^2 + (\sqrt{4})^2 = 3 + 4 = 7 \neq (\sqrt{5})^2$,不能构成直角三角形。
D选项:$1^2 + 3^2 = 1 + 9 = 10 \neq 4^2$,不能构成直角三角形。
结论:A
4. (2024·泰州兴化期末)如图,在平面直角坐标系中,正方形$ABCD的顶点D在y$轴上,且点$A(-6,0),B(4,b)$,则正方形$ABCD$的面积是(

A.80
B.100
C.136
D.156
C
)
A.80
B.100
C.136
D.156
答案:C
解析:
解:设点$D(0,d)$,$O$为坐标原点。
$\because$四边形$ABCD$是正方形,$\therefore AD=AB$,$AD\perp AB$。
$\because A(-6,0)$,$B(4,b)$,$\therefore \overrightarrow{AD}=(6,d)$,$\overrightarrow{AB}=(10,b)$。
$\because AD\perp AB$,$\therefore \overrightarrow{AD}\cdot\overrightarrow{AB}=6×10 + d× b=0$,即$60 + bd=0$,$bd=-60$。
$\because AD=AB$,$\therefore |\overrightarrow{AD}|=|\overrightarrow{AB}|$,$\sqrt{6^{2}+d^{2}}=\sqrt{10^{2}+b^{2}}$,$36 + d^{2}=100 + b^{2}$,$d^{2}-b^{2}=64$。
$\because d^{2}-b^{2}=(d - b)(d + b)=64$,又$d=-\dfrac{60}{b}$,代入得$\left(-\dfrac{60}{b}-b\right)\left(-\dfrac{60}{b}+b\right)=64$,$\left(-\dfrac{b^{2}+60}{b}\right)\left(\dfrac{b^{2}-60}{b}\right)=64$,$-\dfrac{(b^{2}+60)(b^{2}-60)}{b^{2}}=64$,$-\dfrac{b^{4}-3600}{b^{2}}=64$,$-b^{4}+3600=64b^{2}$,$b^{4}+64b^{2}-3600=0$。
设$t=b^{2}(t>0)$,$t^{2}+64t - 3600=0$,解得$t=\dfrac{-64\pm\sqrt{64^{2}+4×3600}}{2}=\dfrac{-64\pm\sqrt{4096 + 14400}}{2}=\dfrac{-64\pm\sqrt{18496}}{2}=\dfrac{-64\pm136}{2}$。
$\because t>0$,$\therefore t=\dfrac{-64 + 136}{2}=36$,即$b^{2}=36$。
$\therefore |AB|^{2}=10^{2}+b^{2}=100 + 36=136$,即正方形$ABCD$的面积是$136$。
C
$\because$四边形$ABCD$是正方形,$\therefore AD=AB$,$AD\perp AB$。
$\because A(-6,0)$,$B(4,b)$,$\therefore \overrightarrow{AD}=(6,d)$,$\overrightarrow{AB}=(10,b)$。
$\because AD\perp AB$,$\therefore \overrightarrow{AD}\cdot\overrightarrow{AB}=6×10 + d× b=0$,即$60 + bd=0$,$bd=-60$。
$\because AD=AB$,$\therefore |\overrightarrow{AD}|=|\overrightarrow{AB}|$,$\sqrt{6^{2}+d^{2}}=\sqrt{10^{2}+b^{2}}$,$36 + d^{2}=100 + b^{2}$,$d^{2}-b^{2}=64$。
$\because d^{2}-b^{2}=(d - b)(d + b)=64$,又$d=-\dfrac{60}{b}$,代入得$\left(-\dfrac{60}{b}-b\right)\left(-\dfrac{60}{b}+b\right)=64$,$\left(-\dfrac{b^{2}+60}{b}\right)\left(\dfrac{b^{2}-60}{b}\right)=64$,$-\dfrac{(b^{2}+60)(b^{2}-60)}{b^{2}}=64$,$-\dfrac{b^{4}-3600}{b^{2}}=64$,$-b^{4}+3600=64b^{2}$,$b^{4}+64b^{2}-3600=0$。
设$t=b^{2}(t>0)$,$t^{2}+64t - 3600=0$,解得$t=\dfrac{-64\pm\sqrt{64^{2}+4×3600}}{2}=\dfrac{-64\pm\sqrt{4096 + 14400}}{2}=\dfrac{-64\pm\sqrt{18496}}{2}=\dfrac{-64\pm136}{2}$。
$\because t>0$,$\therefore t=\dfrac{-64 + 136}{2}=36$,即$b^{2}=36$。
$\therefore |AB|^{2}=10^{2}+b^{2}=100 + 36=136$,即正方形$ABCD$的面积是$136$。
C
5. 正方形$ABCD的边长为4,P$为正方形边上一动点,运动路线是$A \to D \to C \to B \to A,P点经过的路程为x$,以点$A,P,D为顶点的三角形的面积是y$,则下列图象能大致反映$y与x$的函数关系的是(

B
)
答案:B
解析:
情况1:当点P在AD上运动时($0 \leq x \leq 4$)
此时点P与A或D重合,以A,P,D为顶点的三角形不存在,面积$y=0$。
情况2:当点P在DC上运动时($4 < x \leq 8$)
此时$PD = x - 4$,AD为正方形边长(4),三角形APD的面积为:
$y = \frac{1}{2} × AD × PD = \frac{1}{2} × 4 × (x - 4) = 2x - 8$
当$x=4$时,$y=0$;当$x=8$时,$y=8$,函数为一次函数,图像从(4,0)到(8,8)上升。
情况3:当点P在CB上运动时($8 < x \leq 12$)
此时PD为定值(DC=4),三角形APD的面积为:
$y = \frac{1}{2} × AD × DC = \frac{1}{2} × 4 × 4 = 8$
函数值恒为8,图像为水平线段。
情况4:当点P在BA上运动时($12 < x \leq 16$)
此时$AP = 16 - x$,三角形APD的面积为:
$y = \frac{1}{2} × AD × AP = \frac{1}{2} × 4 × (16 - x) = 32 - 2x$
当$x=12$时,$y=8$;当$x=16$时,$y=0$,函数为一次函数,图像从(12,8)到(16,0)下降。
综上,函数图像在$0 \leq x \leq 4$时$y=0$,$4 < x \leq 8$时从0上升到8,$8 < x \leq 12$时恒为8,$12 < x \leq 16$时从8下降到0,符合选项B。
答案:B
此时点P与A或D重合,以A,P,D为顶点的三角形不存在,面积$y=0$。
情况2:当点P在DC上运动时($4 < x \leq 8$)
此时$PD = x - 4$,AD为正方形边长(4),三角形APD的面积为:
$y = \frac{1}{2} × AD × PD = \frac{1}{2} × 4 × (x - 4) = 2x - 8$
当$x=4$时,$y=0$;当$x=8$时,$y=8$,函数为一次函数,图像从(4,0)到(8,8)上升。
情况3:当点P在CB上运动时($8 < x \leq 12$)
此时PD为定值(DC=4),三角形APD的面积为:
$y = \frac{1}{2} × AD × DC = \frac{1}{2} × 4 × 4 = 8$
函数值恒为8,图像为水平线段。
情况4:当点P在BA上运动时($12 < x \leq 16$)
此时$AP = 16 - x$,三角形APD的面积为:
$y = \frac{1}{2} × AD × AP = \frac{1}{2} × 4 × (16 - x) = 32 - 2x$
当$x=12$时,$y=8$;当$x=16$时,$y=0$,函数为一次函数,图像从(12,8)到(16,0)下降。
综上,函数图像在$0 \leq x \leq 4$时$y=0$,$4 < x \leq 8$时从0上升到8,$8 < x \leq 12$时恒为8,$12 < x \leq 16$时从8下降到0,符合选项B。
答案:B
6. 由四舍五入得到的近似数$3.20 × 10^{3}$千米,它是精确到
十
位.答案:十
7. 如图,在平面直角坐标系中,以点$O$为圆心,以$OP$的长为半径画弧,交$x轴的负半轴于点A$,点$A的坐标为(-\sqrt{26},0)$,点$P的纵坐标为-1$,则点$P$的坐标为
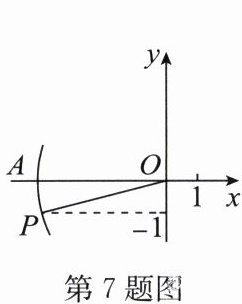
(-5,-1)
.
答案:(-5,-1)
解析:
解:
∵以点$O$为圆心,以$OP$的长为半径画弧,交$x$轴的负半轴于点$A$,
∴$OA = OP$。
∵点$A$的坐标为$(-\sqrt{26},0)$,
∴$OA=\sqrt{26}$,则$OP = \sqrt{26}$。
设点$P$的坐标为$(x,-1)$,
∵点$P$在平面直角坐标系中,
∴由勾股定理得$x^{2}+(-1)^{2}=OP^{2}$,
即$x^{2}+1 = 26$,
$x^{2}=25$,
解得$x=\pm5$。
∵点$P$在第三象限(由图可知点$P$的横坐标为负),
∴$x=-5$,
∴点$P$的坐标为$(-5,-1)$。
$(-5,-1)$
∵以点$O$为圆心,以$OP$的长为半径画弧,交$x$轴的负半轴于点$A$,
∴$OA = OP$。
∵点$A$的坐标为$(-\sqrt{26},0)$,
∴$OA=\sqrt{26}$,则$OP = \sqrt{26}$。
设点$P$的坐标为$(x,-1)$,
∵点$P$在平面直角坐标系中,
∴由勾股定理得$x^{2}+(-1)^{2}=OP^{2}$,
即$x^{2}+1 = 26$,
$x^{2}=25$,
解得$x=\pm5$。
∵点$P$在第三象限(由图可知点$P$的横坐标为负),
∴$x=-5$,
∴点$P$的坐标为$(-5,-1)$。
$(-5,-1)$
8. 如图,点$A(-1,m)在直线y = 2x + 3$上,连接$OA,\angle AOB = 90^{\circ}$,点$B在直线y = -x + b$上,$OA = OB$,则$b = $

2
.
答案:2
解析:
解:
∵点$A(-1,m)$在直线$y=2x+3$上,
∴$m=2×(-1)+3=1$,即$A(-1,1)$。
∴$OA=\sqrt{(-1)^2+1^2}=\sqrt{2}$。
∵$\angle AOB=90°$,$OA=OB$,$OA=\sqrt{2}$,
∴设$B(x,y)$,则$\begin{cases}x^2+y^2=(\sqrt{2})^2 \\ -x+y=0\end{cases}$($OA$斜率为$-1$,$OB$斜率为$1$),
解得$\begin{cases}x=1 \\ y=1\end{cases}$或$\begin{cases}x=-1 \\ y=-1\end{cases}$(舍去,与$A$不关于原点对称且在直线$y=-x+b$右侧)。
∵点$B(1,1)$在直线$y=-x+b$上,
∴$1=-1+b$,解得$b=2$。
2
∵点$A(-1,m)$在直线$y=2x+3$上,
∴$m=2×(-1)+3=1$,即$A(-1,1)$。
∴$OA=\sqrt{(-1)^2+1^2}=\sqrt{2}$。
∵$\angle AOB=90°$,$OA=OB$,$OA=\sqrt{2}$,
∴设$B(x,y)$,则$\begin{cases}x^2+y^2=(\sqrt{2})^2 \\ -x+y=0\end{cases}$($OA$斜率为$-1$,$OB$斜率为$1$),
解得$\begin{cases}x=1 \\ y=1\end{cases}$或$\begin{cases}x=-1 \\ y=-1\end{cases}$(舍去,与$A$不关于原点对称且在直线$y=-x+b$右侧)。
∵点$B(1,1)$在直线$y=-x+b$上,
∴$1=-1+b$,解得$b=2$。
2