25. (10 分)已知当$m$,$n$都是实数,且满足$2m = 8 + n$时,称点$P(m - 1,\frac{n + 2}{2})$为“开心点”。
(1) 判断点$A(5,3)$,$B(4,10)$是否为“开心点”,并说明理由;
(2) 若点$M(a,2a - 1)$是“开心点”,请判断点$M$在第几象限,并说明理由。
(1) 判断点$A(5,3)$,$B(4,10)$是否为“开心点”,并说明理由;
(2) 若点$M(a,2a - 1)$是“开心点”,请判断点$M$在第几象限,并说明理由。
答案:解:
(1)点$A(5,3)$是“开心点”,点$B(4,10)$不是“开心点”,理由如下:
∵$2m = 8 + n$,
∴$n = 2m - 8$.
∴$\frac{n + 2}{2}=\frac{2m - 8 + 2}{2}=m - 3$.
∴点$P(m - 1,\frac{n + 2}{2})$,即$P(m - 1,m - 3)$.
∴“开心点”的特征为横坐标比其纵坐标大2.
∵5比3大2,4比10小6,
∴点$A(5,3)$是“开心点”,点$B(4,10)$不是“开心点”.
(2)由
(1)可知$a = 2a - 1 + 2$,解得$a = -1$,
∴$M(a,2a - 1)$,即$M(-1,-3)$,在第三象限.
(1)点$A(5,3)$是“开心点”,点$B(4,10)$不是“开心点”,理由如下:
∵$2m = 8 + n$,
∴$n = 2m - 8$.
∴$\frac{n + 2}{2}=\frac{2m - 8 + 2}{2}=m - 3$.
∴点$P(m - 1,\frac{n + 2}{2})$,即$P(m - 1,m - 3)$.
∴“开心点”的特征为横坐标比其纵坐标大2.
∵5比3大2,4比10小6,
∴点$A(5,3)$是“开心点”,点$B(4,10)$不是“开心点”.
(2)由
(1)可知$a = 2a - 1 + 2$,解得$a = -1$,
∴$M(a,2a - 1)$,即$M(-1,-3)$,在第三象限.
26. (10 分)如图,$\triangle ABC和\triangle DEF$都是等腰三角形,$AB = AC$,$DE = DF$,$\angle BAC= \angle EDF$,点$E在AB$的延长线上,点$F在射线AC$上,且$AD = AB$。求证:$AE - BC = AF$。
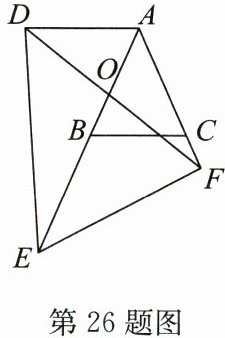

答案:
证明:如答图,在$AE$上取点$M$,使$EM = AF$,连接$DM$.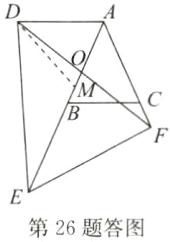
∵$\angle BAC = \angle EDF$,$\angle AOF = \angle DOE$,
∴$\angle DEM = \angle AFD$.又
∵$ED = FD$,$EM = FA$,
∴$\triangle EMD≌\triangle FAD(SAS)$.
∴$DM = DA$,$\angle EDM = \angle FDA$.
∴$\angle EDM + \angle MDF = \angle FDA + \angle MDF$,即$\angle EDF = \angle MDA = \angle BAC$;又
∵$AD = AB$,
∴$\triangle DMA≌\triangle ABC(SAS)$.
∴$AM = BC$;
∵$EM = AE - AM$,
∴$AE - BC = AF$;
证明:如答图,在$AE$上取点$M$,使$EM = AF$,连接$DM$.

∵$\angle BAC = \angle EDF$,$\angle AOF = \angle DOE$,
∴$\angle DEM = \angle AFD$.又
∵$ED = FD$,$EM = FA$,
∴$\triangle EMD≌\triangle FAD(SAS)$.
∴$DM = DA$,$\angle EDM = \angle FDA$.
∴$\angle EDM + \angle MDF = \angle FDA + \angle MDF$,即$\angle EDF = \angle MDA = \angle BAC$;又
∵$AD = AB$,
∴$\triangle DMA≌\triangle ABC(SAS)$.
∴$AM = BC$;
∵$EM = AE - AM$,
∴$AE - BC = AF$;
27. (12 分)某中学为加强新时代中学生劳动教育,开辟了劳动教育实践基地。在基地建设过程中,需要采购煎蛋器和三明治机。经过调查,购买 2 台煎蛋器和 1 台三明治机需 240 元,购买 1 台煎蛋器和 3 台三明治机需 395 元。
(1) 求煎蛋器和三明治机每台价格各是多少元;
(2) 学校准备采购这两种机器共 50 台,其中要求三明治机的台数不少于煎蛋器台数的一半,请你给出最节省费用的购买方案。
(1) 求煎蛋器和三明治机每台价格各是多少元;
(2) 学校准备采购这两种机器共 50 台,其中要求三明治机的台数不少于煎蛋器台数的一半,请你给出最节省费用的购买方案。
答案:解:
(1)设煎蛋器和三明治机每台的价格分别是$x$元、$y$元.根据题意,得$\begin{cases}2x + y = 240\\x + 3y = 395\end{cases}$,解得$\begin{cases}x = 65\\y = 110\end{cases}$.答:煎蛋器和三明治机每台的价格分别是65元、110元.
(2)设总购买费用为$w$元,煎蛋器购买$a$台,则三明治机购买$(50 - a)$台.根据题意,得$w = 65a + 110(50 - a)= - 45a + 5500$,又$50 - a\geq\frac{1}{2}a$,解得$a\leq\frac{100}{3}$,
∵$k = - 45<0$,
∴$w$随着$a$的增大而减小.
∴当$a = 33$时,$w$取最小值为$- 45×33 + 5500 = 4015$元.
∴最节省费用的购买方案为:煎蛋器33台,三明治机17台.
(1)设煎蛋器和三明治机每台的价格分别是$x$元、$y$元.根据题意,得$\begin{cases}2x + y = 240\\x + 3y = 395\end{cases}$,解得$\begin{cases}x = 65\\y = 110\end{cases}$.答:煎蛋器和三明治机每台的价格分别是65元、110元.
(2)设总购买费用为$w$元,煎蛋器购买$a$台,则三明治机购买$(50 - a)$台.根据题意,得$w = 65a + 110(50 - a)= - 45a + 5500$,又$50 - a\geq\frac{1}{2}a$,解得$a\leq\frac{100}{3}$,
∵$k = - 45<0$,
∴$w$随着$a$的增大而减小.
∴当$a = 33$时,$w$取最小值为$- 45×33 + 5500 = 4015$元.
∴最节省费用的购买方案为:煎蛋器33台,三明治机17台.
28. (12 分)
(1) 问题发现:如图①,$\triangle ACB和\triangle DCE$均为等边三角形,点$A$,$D$,$E$在同一直线上,连接$BE$。
填空:①$\angle AEB$的度数为
(2) 拓展探究:如图②,$\triangle ACB和\triangle DCE$均为等腰三角形,$\angle ACB= \angle DCE = 90^{\circ}$,点$A$,$D$,$E$在同一直线上,$CM为\triangle DCE中DE$边上的高,连接$BE$。请判断$\angle AEB的度数及线段CM$,$AE$,$BE$之间的数量关系,并说明理由。
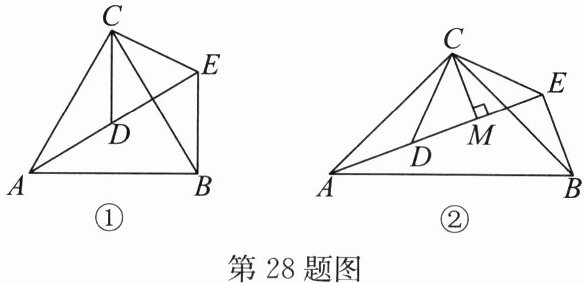
(1) 问题发现:如图①,$\triangle ACB和\triangle DCE$均为等边三角形,点$A$,$D$,$E$在同一直线上,连接$BE$。
填空:①$\angle AEB$的度数为
$60^{\circ}$
,②线段$AD$,$BE$之间的数量关系是______$AD = BE$
;(2) 拓展探究:如图②,$\triangle ACB和\triangle DCE$均为等腰三角形,$\angle ACB= \angle DCE = 90^{\circ}$,点$A$,$D$,$E$在同一直线上,$CM为\triangle DCE中DE$边上的高,连接$BE$。请判断$\angle AEB的度数及线段CM$,$AE$,$BE$之间的数量关系,并说明理由。

答案:
(1)①$60^{\circ}$ ②$AD = BE$
(2)解:$\angle AEB = 90^{\circ}$,$AE = BE + 2CM$,理由如下:
∵$\triangle ACB$和$\triangle DCE$均为等腰三角形,$\angle ACB = \angle DCE = 90^{\circ}$,
∴$AC = BC$,$DC = EC$,$\angle ACB - \angle DCB = \angle DCE - \angle DCB$,即$\angle ACD = \angle BCE$.在$\triangle ACD$和$\triangle BCE$中,$\begin{cases}AC = BC\\\angle ACD = \angle BCE\\CD = CE\end{cases}$,
∴$\triangle ACD≌\triangle BCE(SAS)$.
∴$\angle CAD = \angle CBE$,$AD = BE$;设$AE$与$BC$交于点$O$,则$\angle AOC = \angle BOE$,而$\angle CAD = \angle CBE$,
∴$\angle AEB = \angle ACB = 90^{\circ}$.
∵$CM$为等腰直角三角形$DCE$中斜边$DE$边上的高,
∴$DE = 2CM$.
∵$AE = AD + DE$,
∴$AE = BE + 2CM$.综上,$\angle AEB = 90^{\circ}$,$AE = BE + 2CM$.
(1)①$60^{\circ}$ ②$AD = BE$
(2)解:$\angle AEB = 90^{\circ}$,$AE = BE + 2CM$,理由如下:
∵$\triangle ACB$和$\triangle DCE$均为等腰三角形,$\angle ACB = \angle DCE = 90^{\circ}$,
∴$AC = BC$,$DC = EC$,$\angle ACB - \angle DCB = \angle DCE - \angle DCB$,即$\angle ACD = \angle BCE$.在$\triangle ACD$和$\triangle BCE$中,$\begin{cases}AC = BC\\\angle ACD = \angle BCE\\CD = CE\end{cases}$,
∴$\triangle ACD≌\triangle BCE(SAS)$.
∴$\angle CAD = \angle CBE$,$AD = BE$;设$AE$与$BC$交于点$O$,则$\angle AOC = \angle BOE$,而$\angle CAD = \angle CBE$,
∴$\angle AEB = \angle ACB = 90^{\circ}$.
∵$CM$为等腰直角三角形$DCE$中斜边$DE$边上的高,
∴$DE = 2CM$.
∵$AE = AD + DE$,
∴$AE = BE + 2CM$.综上,$\angle AEB = 90^{\circ}$,$AE = BE + 2CM$.