21. (8 分)已知$5a + 2$的立方根是 3,$3a + b - 1$的算术平方根是 4。
(1) 求$a$,$b$的值;
(2) 求$4a - b$的平方根。
(1) 求$a$,$b$的值;
(2) 求$4a - b$的平方根。
答案:解:
(1)由题意得$\begin{cases}5a + 2 = 27\\3a + b - 1 = 16\end{cases}$,解得$\begin{cases}a = 5\\b = 2\end{cases}$.
(2)由
(1)得$4a - b = 4×5 - 2 = 18$.
∵18的平方根为$\pm\sqrt{18}=\pm3\sqrt{2}$,故$4a - b$的平方根为$\pm3\sqrt{2}$.
(1)由题意得$\begin{cases}5a + 2 = 27\\3a + b - 1 = 16\end{cases}$,解得$\begin{cases}a = 5\\b = 2\end{cases}$.
(2)由
(1)得$4a - b = 4×5 - 2 = 18$.
∵18的平方根为$\pm\sqrt{18}=\pm3\sqrt{2}$,故$4a - b$的平方根为$\pm3\sqrt{2}$.
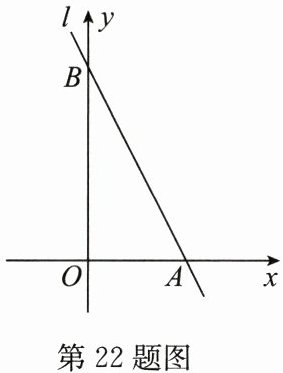
22. (8 分)如图,直线$l是一次函数y = kx + 4$的图象,且直线$l经过点(1,2)$。
(1) 求$k$的值;
(2) 若直线$l分别与x$轴、$y轴相交于A$,$B$两点,求$\triangle AOB$的面积。
(1) 求$k$的值;
(2) 若直线$l分别与x$轴、$y轴相交于A$,$B$两点,求$\triangle AOB$的面积。

答案:解:
(1)
∵直线$y = kx + 4$经过点$(1,2)$,
∴$2 = k + 4$,
∴$k = -2$.
(2)在$y = -2x + 4$中,令$x = 0$,得$y = 4$;令$y = 0$,得$x = 2$.
∴$A(2,0)$,$B(0,4)$,
∴$OA = 2$,$OB = 4$.
∴$S_{\triangle AOB}=\frac{1}{2}OA\cdot OB=\frac{1}{2}×2×4 = 4$.
(1)
∵直线$y = kx + 4$经过点$(1,2)$,
∴$2 = k + 4$,
∴$k = -2$.
(2)在$y = -2x + 4$中,令$x = 0$,得$y = 4$;令$y = 0$,得$x = 2$.
∴$A(2,0)$,$B(0,4)$,
∴$OA = 2$,$OB = 4$.
∴$S_{\triangle AOB}=\frac{1}{2}OA\cdot OB=\frac{1}{2}×2×4 = 4$.
23. (10 分)
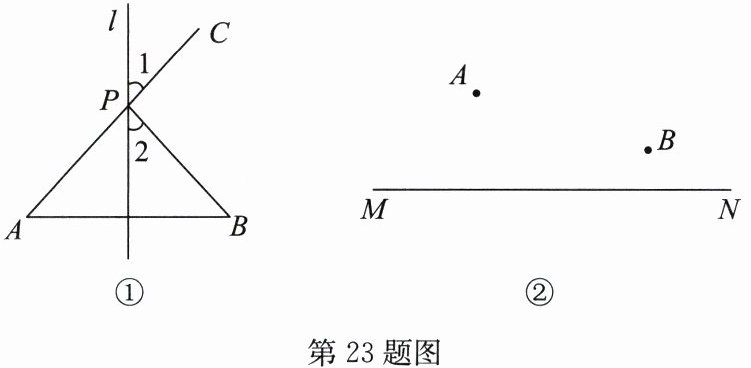
(1) 如图①,直线$l是线段AB$的垂直平分线,在$l上取一点P$,连接$BP$,$AP$,并延长$AP到点C$,判断$\angle 1与\angle 2$的大小关系,并说明理由;
(2) 尺规作图:如图②,点$A$,$B是直线MN$外同侧的两点,请用无刻度的直尺和圆规在直线$MN上求作一点P$,使得$\angle APM= \angle BPN$。(保留作图痕迹,不写作法)
(1) 如图①,直线$l是线段AB$的垂直平分线,在$l上取一点P$,连接$BP$,$AP$,并延长$AP到点C$,判断$\angle 1与\angle 2$的大小关系,并说明理由;
(2) 尺规作图:如图②,点$A$,$B是直线MN$外同侧的两点,请用无刻度的直尺和圆规在直线$MN上求作一点P$,使得$\angle APM= \angle BPN$。(保留作图痕迹,不写作法)

答案:
(1)$\angle 1 = \angle 2$,理由:设直线$l$交$AB$于点$O$,如答图①.
∵直线$l$是线段$AB$的垂直平分线,
∴$PA = PB$,$PO\perp AB$,
∴$\angle APO = \angle 2$,又
∵$\angle APO = \angle 1$,
∴$\angle 1 = \angle 2$.
(2)如答图②,点$P$即为所作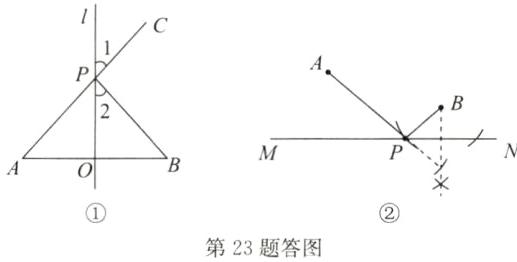
(1)$\angle 1 = \angle 2$,理由:设直线$l$交$AB$于点$O$,如答图①.
∵直线$l$是线段$AB$的垂直平分线,
∴$PA = PB$,$PO\perp AB$,
∴$\angle APO = \angle 2$,又
∵$\angle APO = \angle 1$,
∴$\angle 1 = \angle 2$.
(2)如答图②,点$P$即为所作

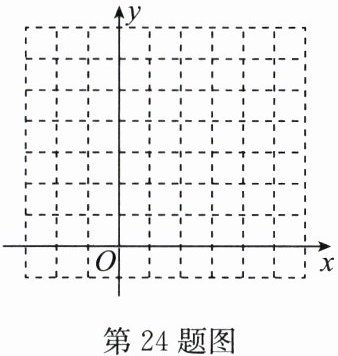
24. (10 分)在如图所示的平面直角坐标系中,每个小方格的边长表示 1 个单位长度,将$\triangle ABC平移后得到\triangle A'B'C'$,它们的三个顶点坐标如下表。

(1) 观察表中各对应点坐标的变化,填空:$a = $______,$b = $______;
(2) 在图中画出$\triangle A'B'C'$;
(3) 求出线段$AB$在整个平移的过程中在坐标平面上扫过的面积。

(1) 观察表中各对应点坐标的变化,填空:$a = $______,$b = $______;
(2) 在图中画出$\triangle A'B'C'$;
(3) 求出线段$AB$在整个平移的过程中在坐标平面上扫过的面积。

答案:
(1)−3 3
(2)解:如答图所示.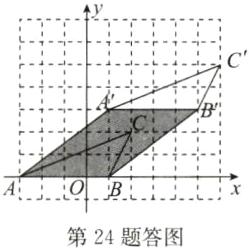
(3)解:如答图,线段$AB$在整个平移的过程中扫过的图形是平行四边形$A'B'BA$,其面积为$4×3 = 12$.
(1)−3 3
(2)解:如答图所示.

(3)解:如答图,线段$AB$在整个平移的过程中扫过的图形是平行四边形$A'B'BA$,其面积为$4×3 = 12$.