10. 已知点$A(1,a)和点B( - 2,b)是一次函数y = - \frac{1}{2}x + c$图象上的两点,则$a$
<
$b$。(填“$>$”“$<$”或“$=$”)答案:<
解析:
∵一次函数$y = -\frac{1}{2}x + c$中,$k=-\frac{1}{2}<0$,
∴$y$随$x$的增大而减小。
∵点$A(1,a)$和点$B(-2,b)$在该函数图象上,且$1>-2$,
∴$a<b$。
<
11. 某市的市域面积约为 16972 平方千米,数据 16972 用四舍五入法精确到千位,并用科学记数法表示为
$1.7× 10^{4}$
。答案:$1.7× 10^{4}$
解析:
$1.7× 10^{4}$
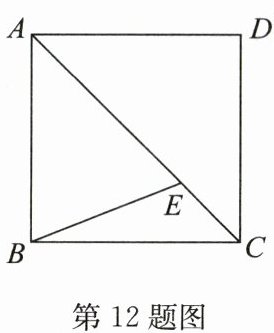
12. 如图,在正方形$ABCD$中,$E为对角线AC$上一点,且$AE = AB$,则$\angle BEA$的度数是______$^{\circ}$。

67.5
答案:67.5
解析:
解:在正方形$ABCD$中,$AB=BC=CD=AD$,$\angle ABC=90^{\circ}$,对角线$AC$平分$\angle BAD$和$\angle BCD$,故$\angle BAC = 45^{\circ}$。
因为$AE = AB$,所以$\triangle ABE$是等腰三角形,$\angle ABE=\angle AEB$。
在$\triangle ABE$中,$\angle BAC + \angle ABE + \angle AEB=180^{\circ}$,即$45^{\circ}+2\angle AEB=180^{\circ}$,解得$\angle AEB=\frac{180^{\circ}-45^{\circ}}{2}=67.5^{\circ}$。
$67.5$
因为$AE = AB$,所以$\triangle ABE$是等腰三角形,$\angle ABE=\angle AEB$。
在$\triangle ABE$中,$\angle BAC + \angle ABE + \angle AEB=180^{\circ}$,即$45^{\circ}+2\angle AEB=180^{\circ}$,解得$\angle AEB=\frac{180^{\circ}-45^{\circ}}{2}=67.5^{\circ}$。
$67.5$
13. 在$\triangle ABC$中,$AC = 6$,$BC = 8$,$AB = 10$,$D为AB$的中点,则$CD$的长为
5
。答案:5
解析:
在$\triangle ABC$中,$AC=6$,$BC=8$,$AB=10$。
因为$AC^2 + BC^2 = 6^2 + 8^2 = 36 + 64 = 100$,$AB^2 = 10^2 = 100$,所以$AC^2 + BC^2 = AB^2$,故$\triangle ABC$是直角三角形,且$\angle ACB = 90°$。
又因为$D$为$AB$的中点,直角三角形斜边中线等于斜边的一半,所以$CD = \frac{1}{2}AB = \frac{1}{2} × 10 = 5$。
5
因为$AC^2 + BC^2 = 6^2 + 8^2 = 36 + 64 = 100$,$AB^2 = 10^2 = 100$,所以$AC^2 + BC^2 = AB^2$,故$\triangle ABC$是直角三角形,且$\angle ACB = 90°$。
又因为$D$为$AB$的中点,直角三角形斜边中线等于斜边的一半,所以$CD = \frac{1}{2}AB = \frac{1}{2} × 10 = 5$。
5
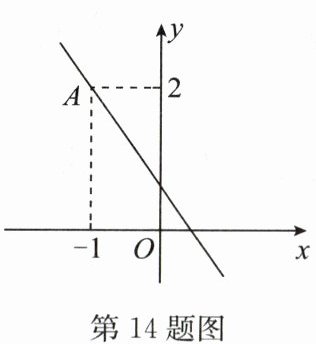
14. 如图,一次函数$y = kx + b的图象经过点A( - 1,2)$,则不等式$kx + b<2$的解集为
$x>-1$
。
答案:$x>-1$
解析:
解:因为一次函数$y = kx + b$的图象经过点$A(-1,2)$,观察图象可知,当$x > -1$时,函数值$y < 2$,所以不等式$kx + b < 2$的解集为$x > -1$。
$x > -1$
$x > -1$
15. 如图为 8 个全等的正六边形紧密排列在同一平面上的情形,根据图中标示的各点位置,请写出与$\triangle ACD$全等的三角形:
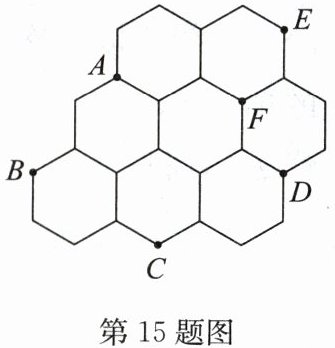
$\triangle AED$
。
答案:$\triangle AED$
16. 已知点$P$在第四象限,且到$x$轴的距离为 2,到$y$轴的距离是 4,则点$P$的坐标为
$(4,-2)$
。答案:$(4,-2)$
17. 已知等腰三角形的两边长分别为$a$,$b$,且$a$,$b满足(a - 2)^2+\vert b - 5\vert = 0$,则此三角形的周长为
12
。答案:12
解析:
因为$(a - 2)^2 + |b - 5| = 0$,所以$a - 2 = 0$,$b - 5 = 0$,解得$a = 2$,$b = 5$。
情况一:若腰长为$2$,底边长为$5$,则$2 + 2 = 4 < 5$,不满足三角形两边之和大于第三边,舍去。
情况二:若腰长为$5$,底边长为$2$,则$5 + 2 > 5$,$5 + 5 > 2$,满足三角形三边关系。此时周长为$5 + 5 + 2 = 12$。
12
情况一:若腰长为$2$,底边长为$5$,则$2 + 2 = 4 < 5$,不满足三角形两边之和大于第三边,舍去。
情况二:若腰长为$5$,底边长为$2$,则$5 + 2 > 5$,$5 + 5 > 2$,满足三角形三边关系。此时周长为$5 + 5 + 2 = 12$。
12
18. 在平面直角坐标系$xOy$中,一次函数$y = - \frac{4}{3}x + 4的图象与x$轴、$y轴分别相交于点A$,$B$。若点$P(m,m - 1)在\triangle AOB$的内部,则$m$的取值范围是
$1<m<\frac{15}{7}$
。答案:$1<m<\frac{15}{7}$
解析:
当$y=0$时,$-\frac{4}{3}x + 4=0$,解得$x=3$,则$A(3,0)$;当$x=0$时,$y=4$,则$B(0,4)$。
点$P(m,m - 1)$在$\triangle AOB$内部,需满足:
1. $m>0$(在$y$轴右侧);
2. $m - 1>0$(在$x$轴上方),即$m>1$;
3. $m<3$(在$A$点左侧);
4. 点$P$在直线$AB$下方:$m - 1<-\frac{4}{3}m + 4$,解得$m<\frac{15}{7}$。
综上,$1<m<\frac{15}{7}$。
点$P(m,m - 1)$在$\triangle AOB$内部,需满足:
1. $m>0$(在$y$轴右侧);
2. $m - 1>0$(在$x$轴上方),即$m>1$;
3. $m<3$(在$A$点左侧);
4. 点$P$在直线$AB$下方:$m - 1<-\frac{4}{3}m + 4$,解得$m<\frac{15}{7}$。
综上,$1<m<\frac{15}{7}$。
19. (8 分)
(1) 计算:$- 1^{2023}+(\sqrt{5} - π)^0+\sqrt[3]{27}$;
(2) 求$x$的值:$(x - 1)^2 - 9 = 0$。
(1) 计算:$- 1^{2023}+(\sqrt{5} - π)^0+\sqrt[3]{27}$;
(2) 求$x$的值:$(x - 1)^2 - 9 = 0$。
答案:
(1)3
(2)$x=4$或$x=-2$
(1)3
(2)$x=4$或$x=-2$
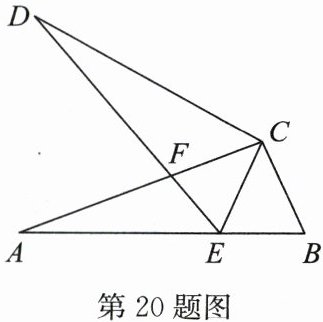
20. (8 分)如图,点$E在线段AB$上,$AC与DE相交于点F$,$\triangle ABC\cong\triangle DEC$,$\angle B = 65^{\circ}$。
(1) 求$\angle DCA$的度数;
(2) 若$\angle A = 20^{\circ}$,求$\angle DFA$的度数。
(1) 求$\angle DCA$的度数;
(2) 若$\angle A = 20^{\circ}$,求$\angle DFA$的度数。

答案:解:
(1)
∵$\triangle ABC≌\triangle DEC$,
∴$CB=CE$,$\angle A=\angle D$,$\angle ACB=\angle DCE$;
∴$\angle ACB-\angle ACE=\angle DCE-\angle ACE$,即$\angle DCA=\angle BCE$.
∵$CB=CE$,
∴$\angle B=\angle CEB=65^{\circ}$.
∴$\angle BCE=180^{\circ}-\angle B-\angle CEB=50^{\circ}$.
∴$\angle DCA=50^{\circ}$.
(2)
∵$\angle A=20^{\circ}=\angle D$,$\angle DCA=50^{\circ}$,
∴$\angle DFA=\angle D+\angle DCA=20^{\circ}+50^{\circ}=70^{\circ}$.
(1)
∵$\triangle ABC≌\triangle DEC$,
∴$CB=CE$,$\angle A=\angle D$,$\angle ACB=\angle DCE$;
∴$\angle ACB-\angle ACE=\angle DCE-\angle ACE$,即$\angle DCA=\angle BCE$.
∵$CB=CE$,
∴$\angle B=\angle CEB=65^{\circ}$.
∴$\angle BCE=180^{\circ}-\angle B-\angle CEB=50^{\circ}$.
∴$\angle DCA=50^{\circ}$.
(2)
∵$\angle A=20^{\circ}=\angle D$,$\angle DCA=50^{\circ}$,
∴$\angle DFA=\angle D+\angle DCA=20^{\circ}+50^{\circ}=70^{\circ}$.