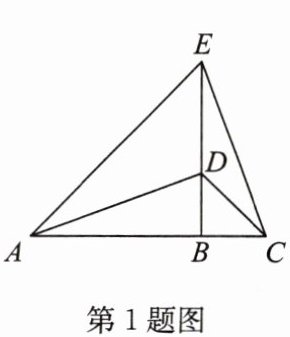
1. 如图,$\triangle ABD\cong\triangle EBC$,$AB = 12$,$BC = 5$,$A$,$B$,$C$三点共线,则下列结论:①$CD\perp AE$;②$AD\perp CE$;③$ED = 8$;④$\angle EAD= \angle ECD$. 其中,正确的是( )
A.①②
B.①②④
C.②④
D.②③④

A.①②
B.①②④
C.②④
D.②③④
答案:
B 点拨:如答图,延长AD交CE于点H,延长CD交AE于点F.
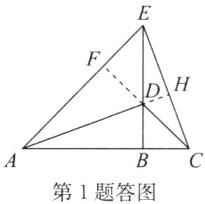
∵△ABD≌△EBC,
∴EB=AB=12,BD=BC=5,∠BAD=∠BEC,∠ABE=∠CBE=90°,∠ADB=∠BCE;
∴∠CAE=∠AEB=45°=∠BCD=∠BDC,∠BEC+∠ACE=90°.ED=EB−BD=7.故③错误.
∴∠CAE+∠BCD=90°,∠BAD+∠ACE=∠BEC+∠ACE=90°,
∴CD⊥AE,AD⊥CE.故①②正确
∵∠EAD=∠ADB−∠AED=∠ADB−45°,∠ECD=∠ACE−∠ACD=∠ACE−45°,
∴∠EAD=∠ECD.故④正确.故选B.
B 点拨:如答图,延长AD交CE于点H,延长CD交AE于点F.

∵△ABD≌△EBC,
∴EB=AB=12,BD=BC=5,∠BAD=∠BEC,∠ABE=∠CBE=90°,∠ADB=∠BCE;
∴∠CAE=∠AEB=45°=∠BCD=∠BDC,∠BEC+∠ACE=90°.ED=EB−BD=7.故③错误.
∴∠CAE+∠BCD=90°,∠BAD+∠ACE=∠BEC+∠ACE=90°,
∴CD⊥AE,AD⊥CE.故①②正确
∵∠EAD=∠ADB−∠AED=∠ADB−45°,∠ECD=∠ACE−∠ACD=∠ACE−45°,
∴∠EAD=∠ECD.故④正确.故选B.
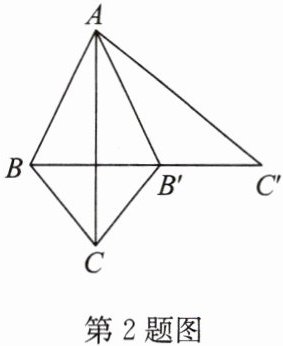
2. 如图,将$\triangle ABC沿AC所在的直线翻折得到\triangle AB'C$,再将$\triangle AB'C沿AB'所在的直线翻折得到\triangle AB'C'$. 若点$B$,$B'$,$C'$在同一条直线上,$\angle BAC= \alpha$. 有下列结论:①$\triangle AB'C'\cong\triangle ABC$;②$BB'\perp AC$;③$\angle CB'B = 2\alpha$. 其中,正确的说法是
①②③
.(填序号)
答案:①②③ 点拨:①由翻折可知△ABC≌△AB'C,△AB'C≌△AB'C',
∴△ABC≌△AB'C'.故①正确.
②由翻折可知点B与点B'关于直线AC对称,
∴AC⊥BB'.故②正确.
③由翻折可知∠B'AC'=∠B'AC=∠BAC=α,∠AB'C'=∠AB'C.
∵AC⊥BB',
∴∠AB'B=90°−∠B'AC=90°−α.
∴∠AB'C'=180°−∠AB'B=180°−(90°−α)=90°+α.
∴∠AB'C=90°+α.
∴∠CB'B=∠AB'C−∠AB'B=90°+α−(90°−α)=2α.
故③正确.
综上所述,正确的说法是①②③.
∴△ABC≌△AB'C'.故①正确.
②由翻折可知点B与点B'关于直线AC对称,
∴AC⊥BB'.故②正确.
③由翻折可知∠B'AC'=∠B'AC=∠BAC=α,∠AB'C'=∠AB'C.
∵AC⊥BB',
∴∠AB'B=90°−∠B'AC=90°−α.
∴∠AB'C'=180°−∠AB'B=180°−(90°−α)=90°+α.
∴∠AB'C=90°+α.
∴∠CB'B=∠AB'C−∠AB'B=90°+α−(90°−α)=2α.
故③正确.
综上所述,正确的说法是①②③.
3. 如图,已知$\triangle ABC\cong\triangle DEF$,$DF// BC$,且$\angle B = 60^{\circ}$,$\angle F = 40^{\circ}$,点$A在DE$上,求$\angle BAD$的度数.
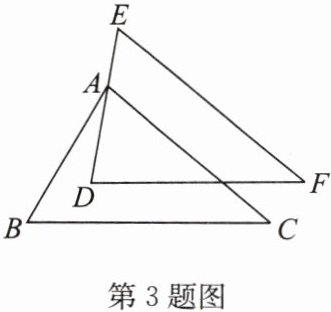

答案:解:设DF与AC交于点P.
∵△ABC≌△DEF,
∴∠B=∠E=60°,∠C=∠F=40°.
∵DF//BC,
∴∠APD=∠C=40°.
∴∠APD=∠F;
∴AC//EF.
∴∠DAC=∠E=60°.
∵∠BAC=180°−∠B−∠C=180°−60°−40°=80°,
∴∠BAD=∠BAC−∠DAC=80°−60°=20°.
∵△ABC≌△DEF,
∴∠B=∠E=60°,∠C=∠F=40°.
∵DF//BC,
∴∠APD=∠C=40°.
∴∠APD=∠F;
∴AC//EF.
∴∠DAC=∠E=60°.
∵∠BAC=180°−∠B−∠C=180°−60°−40°=80°,
∴∠BAD=∠BAC−∠DAC=80°−60°=20°.