1. 如图,在四边形 BEFC 中,D 为 BC 边的中点,∠EDF = 90°,关于 BE + FC 与 EF 的大小关系正确的是( )

A.BE + FC < EF
B.BE + FC = EF
C.BE + FC > EF
D.无法确定

A.BE + FC < EF
B.BE + FC = EF
C.BE + FC > EF
D.无法确定
答案:
1. C 点拨:如答图,延长 FD 至点 A,使 DA=DF,连接 AB,AE.
∵∠EDF=90°,
∴∠ADE=180° - 90°=90°.
又
∵DE=DE,DA=DF,
∴△EDA≌△EDF(SAS).
∴EF=EA.
∵D 为 BC 边的中点,
∴BD=CD.
在△ADB≌△FDC 中,$\left\{\begin{array}{l} BD=CD,\\ ∠ADB=∠FDC,\\ AD=FD,\end{array}\right. $
∴△ADB≌△FDC(SAS).
∴AB=FC.
在△ABE 中,AB+BE>AE,
∴BE+FC>EF.
故选 C.

1. C 点拨:如答图,延长 FD 至点 A,使 DA=DF,连接 AB,AE.
∵∠EDF=90°,
∴∠ADE=180° - 90°=90°.
又
∵DE=DE,DA=DF,
∴△EDA≌△EDF(SAS).
∴EF=EA.
∵D 为 BC 边的中点,
∴BD=CD.
在△ADB≌△FDC 中,$\left\{\begin{array}{l} BD=CD,\\ ∠ADB=∠FDC,\\ AD=FD,\end{array}\right. $
∴△ADB≌△FDC(SAS).
∴AB=FC.
在△ABE 中,AB+BE>AE,
∴BE+FC>EF.
故选 C.

2. 如图,在△ABC 中,D 是 BC 边的中点.
(1)求证:AB + AC > 2AD;
(2)若 AB = 5,AC = 7,求 AD 长的取值范围.

(1)求证:AB + AC > 2AD;
(2)若 AB = 5,AC = 7,求 AD 长的取值范围.

答案:
2.
(1)证明:如答图,延长 AD 至点 E,使 DE=AD,连接 CE.
∵D 是 BC 边的中点,
∴BD=CD.
又
∵∠ADB=∠EDC,AD=DE,
∴△ADB≌△EDC(SAS).
∴AB=EC.
在△ACE 中,AC+CE>AE,
∴AB+AC>2AD.

(2)解:在△ACE 中,AC=7,
CE=AB=5,AC - CE<AE<AC+CE,
∴7 - 5<2AD<7+5.
∴1<AD<6.
2.
(1)证明:如答图,延长 AD 至点 E,使 DE=AD,连接 CE.
∵D 是 BC 边的中点,
∴BD=CD.
又
∵∠ADB=∠EDC,AD=DE,
∴△ADB≌△EDC(SAS).
∴AB=EC.
在△ACE 中,AC+CE>AE,
∴AB+AC>2AD.

(2)解:在△ACE 中,AC=7,
CE=AB=5,AC - CE<AE<AC+CE,
∴7 - 5<2AD<7+5.
∴1<AD<6.
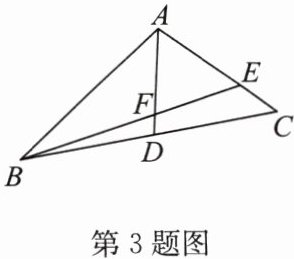
3. 如图,在△ABC 中,BD = CD,BE 交 AD 于点 F,AE = EF. 若 BE = 7CE,AE = $\frac{5}{2}$,求 BF 的长.

答案:
3. 解:如答图,延长 AD 至点 G,使 DG=AD,连接 BG.
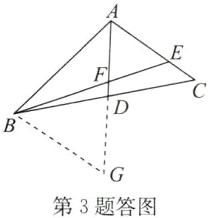
在△BDG 和△CDA 中,$\left\{\begin{array}{l} BD=CD,\\ ∠BDG=∠CDA,\\ GD=AD,\end{array}\right. $
∴△BDG≌△CDA(SAS).
∴BG=AC,∠CAD=∠G.
又
∵AE=EF,
∴∠CAD=∠AFE.
又
∵∠BFG=∠AFE,
∴∠G=∠BFG,
∴BG=BF,
∴AC=BF.
∵BE=7CE,AE=$\frac{5}{2}$,
∴BF+EF=BE=7(AC - AE),
即 BF+$\frac{5}{2}$=7($BF-\frac{5}{2}$),
∴BF=$\frac{10}{3}$.
3. 解:如答图,延长 AD 至点 G,使 DG=AD,连接 BG.

在△BDG 和△CDA 中,$\left\{\begin{array}{l} BD=CD,\\ ∠BDG=∠CDA,\\ GD=AD,\end{array}\right. $
∴△BDG≌△CDA(SAS).
∴BG=AC,∠CAD=∠G.
又
∵AE=EF,
∴∠CAD=∠AFE.
又
∵∠BFG=∠AFE,
∴∠G=∠BFG,
∴BG=BF,
∴AC=BF.
∵BE=7CE,AE=$\frac{5}{2}$,
∴BF+EF=BE=7(AC - AE),
即 BF+$\frac{5}{2}$=7($BF-\frac{5}{2}$),
∴BF=$\frac{10}{3}$.