1. 如图,在四边形 $ABCD$ 中,$AB = AD$,$AC = 5$,$\angle DAB = \angle DCB = 90^{\circ}$,则四边形 $ABCD$ 的面积为( )

A.15
B.12.5
C.14.5
D.17

A.15
B.12.5
C.14.5
D.17
答案:
B 点拨:如答图,过点A作AE⊥AC,交CB的延长线于点E.

∵∠DAB=∠DCB=90°,
∴∠D+∠ABC=180°=∠ABE+∠ABC.
∴∠D=∠ABE.
又
∵∠DAB=∠CAE=90°,
∴∠CAD+∠CAB=∠EAB+∠CAB,
∴∠CAD=∠EAB.
在△ACD和△AEB中,{∠D=∠ABE,AD=AB,∠DAC=∠BAE,
∴△ACD≌△AEB(ASA),
∴AC=AE,即△ACE是等腰直角三角形.
∴四边形ABCD的面积与△ACE的面积相等.
∵S△ACE=$\frac{1}{2}$×5×5=12.5,
∴四边形ABCD的面积为12.5.故选B
B 点拨:如答图,过点A作AE⊥AC,交CB的延长线于点E.

∵∠DAB=∠DCB=90°,
∴∠D+∠ABC=180°=∠ABE+∠ABC.
∴∠D=∠ABE.
又
∵∠DAB=∠CAE=90°,
∴∠CAD+∠CAB=∠EAB+∠CAB,
∴∠CAD=∠EAB.
在△ACD和△AEB中,{∠D=∠ABE,AD=AB,∠DAC=∠BAE,
∴△ACD≌△AEB(ASA),
∴AC=AE,即△ACE是等腰直角三角形.
∴四边形ABCD的面积与△ACE的面积相等.
∵S△ACE=$\frac{1}{2}$×5×5=12.5,
∴四边形ABCD的面积为12.5.故选B
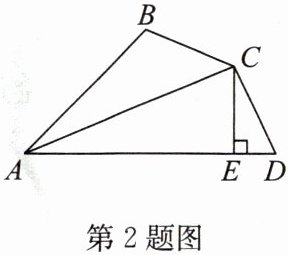
2. 如图,$AC$ 平分 $\angle BAD$,$\angle B + \angle D = 180^{\circ}$,$CE \perp AD$ 于点 $E$,$AD = 10$ cm,$AB = 7$ cm,那么 $DE$ 的长度为______cm.

答案:
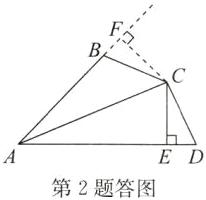
1.5 点拨:如答图,过点C作CF⊥AB,交AB的延长线于点F.
∵AC平分∠BAD,CE⊥AD,CF⊥AB,
∴∠CAE=∠CAF,∠CEA=∠CFA=90°.
在△AEC和△AFC中,{∠CAE=∠CAF,∠CEA=∠CFA,AC=AC,
∴△AEC≌△AFC(AAS).
∴AE=AF,CE=CF.
∵∠ABC+∠D=180°,∠ABC+∠CBF=180°,
∴∠D=∠CBF.
在△CED和△CFB中,{∠D=∠CBF,∠CED=∠CFB,CE=CF,
∴△CED≌△CFB(AAS).
∴DE=BF.
∴AD - DE=AB+BF=AB+DE.
∵AD=10cm,AB=7cm,
∴DE=1.5cm.
1.5 点拨:如答图,过点C作CF⊥AB,交AB的延长线于点F.
∵AC平分∠BAD,CE⊥AD,CF⊥AB,
∴∠CAE=∠CAF,∠CEA=∠CFA=90°.
在△AEC和△AFC中,{∠CAE=∠CAF,∠CEA=∠CFA,AC=AC,
∴△AEC≌△AFC(AAS).
∴AE=AF,CE=CF.
∵∠ABC+∠D=180°,∠ABC+∠CBF=180°,
∴∠D=∠CBF.
在△CED和△CFB中,{∠D=∠CBF,∠CED=∠CFB,CE=CF,
∴△CED≌△CFB(AAS).
∴DE=BF.
∴AD - DE=AB+BF=AB+DE.
∵AD=10cm,AB=7cm,
∴DE=1.5cm.

3. 如图,在 $\triangle ABC$ 中,$AB = AC$,$\angle BAC = 90^{\circ}$,$CD$ 平分 $\angle ACB$,$BE \perp CD$,垂足 $E$ 在 $CD$ 的延长线上,求证:$CD = 2BE$.


答案:
证明:如答图,延长CA,BE相交于点M.

∵BE⊥CD,
∴∠BEC=∠MEC=90°,
∵∠BAC=90°,
∴∠BAM=∠BAC=90°.
∵∠EDB=∠ADC,
∴∠ABM=∠ACD.
在△ABM与△ACD中,{∠ABM=∠ACD,AB=AC,∠MAB=∠DAC,
∴△ABM≌△ACD(ASA),
∴BM=CD.
∵CD平分∠ACB,
∴∠MCE=∠BCE.
在△MCE与△BCE中,{∠MCE=∠BCE,CE=CE,∠MEC=∠BEC,
∴△MCE≌△BCE(ASA),
∴BE=EM,
∴CD=BM=2BE.
证明:如答图,延长CA,BE相交于点M.

∵BE⊥CD,
∴∠BEC=∠MEC=90°,
∵∠BAC=90°,
∴∠BAM=∠BAC=90°.
∵∠EDB=∠ADC,
∴∠ABM=∠ACD.
在△ABM与△ACD中,{∠ABM=∠ACD,AB=AC,∠MAB=∠DAC,
∴△ABM≌△ACD(ASA),
∴BM=CD.
∵CD平分∠ACB,
∴∠MCE=∠BCE.
在△MCE与△BCE中,{∠MCE=∠BCE,CE=CE,∠MEC=∠BEC,
∴△MCE≌△BCE(ASA),
∴BE=EM,
∴CD=BM=2BE.