1. 将函数 $ y = 2x - 1 $ 的图象位于 $ x $ 轴下方的部分沿 $ x $ 轴翻折至其上方,所得的折线是函数 $ y = |2x - 1| $ 的图象,与直线 $ y = x + b $ 的图象交点的横坐标 $ x $ 均满足 $ -1 < x < 2 $,则 $ b $ 的取值范围为( )
A.$ b < 1 $
B.$ -\frac{1}{2} \leq b < 1 $
C.$ 1 < b < 4 $
D.$ 0 \leq b < 1 $
A.$ b < 1 $
B.$ -\frac{1}{2} \leq b < 1 $
C.$ 1 < b < 4 $
D.$ 0 \leq b < 1 $
答案:
B 点拨:如答图,所得的折线的函数表达式为$y=\left\{\begin{array}{l} -2x+1\left(x<\frac {1}{2}\right),\\ 2x-1\left(x\geqslant \frac {1}{2}\right).\end{array}\right.$

当$x=-1$时,$y=-2×(-1)+1=3$,即$A(-1,3);$
当$x=2$时,$y=4-1=3$,即$B(2,3);$
当$y=0$时,$x=0.5$,即$C(0.5,0).$
把$(-1,3)$代入$y=x+b$中,可得$b=4;$
把$(2,3)$代入$y=x+b$中,可得$b=1;$
把$(0.5,0)$代入$y=x+b$中,可得$b=-\frac {1}{2}.$
∵函数$y=|2x-1|$的图象与直线$y=x+b$的图象交点的横坐标$x$均满足$-1<x<2,\therefore \left\{\begin{array}{l} b<4,\\ b<1,\\ b\geqslant -\frac {1}{2},\end{array}\right. $
即$-\frac {1}{2}\leqslant b<1$.故选 B.
B 点拨:如答图,所得的折线的函数表达式为$y=\left\{\begin{array}{l} -2x+1\left(x<\frac {1}{2}\right),\\ 2x-1\left(x\geqslant \frac {1}{2}\right).\end{array}\right.$

当$x=-1$时,$y=-2×(-1)+1=3$,即$A(-1,3);$
当$x=2$时,$y=4-1=3$,即$B(2,3);$
当$y=0$时,$x=0.5$,即$C(0.5,0).$
把$(-1,3)$代入$y=x+b$中,可得$b=4;$
把$(2,3)$代入$y=x+b$中,可得$b=1;$
把$(0.5,0)$代入$y=x+b$中,可得$b=-\frac {1}{2}.$
∵函数$y=|2x-1|$的图象与直线$y=x+b$的图象交点的横坐标$x$均满足$-1<x<2,\therefore \left\{\begin{array}{l} b<4,\\ b<1,\\ b\geqslant -\frac {1}{2},\end{array}\right. $
即$-\frac {1}{2}\leqslant b<1$.故选 B.
2. 已知一次函数 $ y = \frac{1}{2}x + 1 $ 的图象与 $ y $ 轴交于点 $ A $,与 $ x $ 轴交于点 $ B $,将该函数的图象绕点 $ A $ 旋转 $ 45° $,旋转后的图象对应的函数关系式是______.
答案:
$y=-\frac {1}{3}x+1$或$y=3x+1$ 点拨:
∵一次函数$y=\frac {1}{2}x+1$的图象与$y$轴交于点$A$,与$x$轴交于点$B$,
∴$A(0,1)$,$B(-2,0).$
如答图①,当直线$y=\frac {1}{2}x+1$绕点$A$顺时针旋转$45^{\circ }$后的图象为直线$l_{1}$,过点$B$作$BD⊥$直线$l_{1}$于点$D$,过点$D$作$DF⊥y$轴于点$F$,过点$B$作$BE⊥FD$交$FD$的延长线于点$E$,则$△ABD$为等腰直角三角形,$\therefore AD=BD.$
$\because ∠FDA+∠FAD=∠FDA+∠EDB=90^{\circ },$
$\therefore ∠FAD=∠EDB.$
又$\because ∠AFD=∠E=90^{\circ },\therefore △ADF\cong △DBE(AAS).$
设$AF=a$,则$DE=a.$
∵点$A(0,1)$,点$B(-2,0),$
$\therefore DF=BE=OF=1+a,EF=ED+DF=a+1+a=OB=2,$
$\therefore a=\frac {1}{2},\therefore DF=OF=1+a=\frac {3}{2}.$
$\therefore D(-\frac {3}{2},\frac {3}{2}).$
设直线$l_{1}$的函数表达式为$y=kx+1$,则$\frac {3}{2}=-\frac {3}{2}k+1,$
解得$k=-\frac {1}{3}$,
∴直线$l_{1}$的函数表达式为$y=-\frac {1}{3}x+1.$
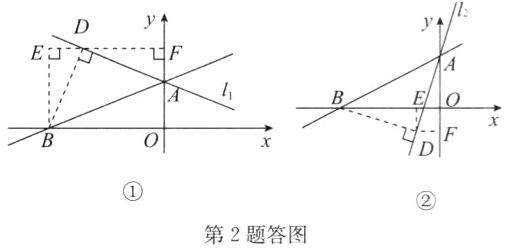
如答图②,直线$y=\frac {1}{2}x+1$绕点$A$逆时针旋转$45^{\circ }$后的图象为直线$l_{2}$,过点$B$作$BD⊥$直线$l_{2}$于点$D$,过点$D$作$DF⊥y$轴于点$F$,作$DE⊥x$轴于点$E$,则$△ABD$为等腰直角三角形.
同理可证$△ADF\cong △BDE.$
设$DF=b$,则$DE=b.$
∵点$A(0,1)$,点$B(-2,0),$
$\therefore AF=BE=1+b,BO=BE+OE=b+1+b=2,$
$\therefore b=\frac {1}{2},\therefore D(-\frac {1}{2},-\frac {1}{2}).$
设直线$l_{2}$的函数表达式为$y=kx+1,$
则$-\frac {1}{2}=-\frac {1}{2}k+1$,解得$k=3,$
∴直线$l_{2}$的函数表达式为$y=3x+1.$
综上可知,旋转后的函数图象对应的函数关系式是$y=-\frac {1}{3}x+1$或$y=3x+1.$
$y=-\frac {1}{3}x+1$或$y=3x+1$ 点拨:
∵一次函数$y=\frac {1}{2}x+1$的图象与$y$轴交于点$A$,与$x$轴交于点$B$,
∴$A(0,1)$,$B(-2,0).$
如答图①,当直线$y=\frac {1}{2}x+1$绕点$A$顺时针旋转$45^{\circ }$后的图象为直线$l_{1}$,过点$B$作$BD⊥$直线$l_{1}$于点$D$,过点$D$作$DF⊥y$轴于点$F$,过点$B$作$BE⊥FD$交$FD$的延长线于点$E$,则$△ABD$为等腰直角三角形,$\therefore AD=BD.$
$\because ∠FDA+∠FAD=∠FDA+∠EDB=90^{\circ },$
$\therefore ∠FAD=∠EDB.$
又$\because ∠AFD=∠E=90^{\circ },\therefore △ADF\cong △DBE(AAS).$
设$AF=a$,则$DE=a.$
∵点$A(0,1)$,点$B(-2,0),$
$\therefore DF=BE=OF=1+a,EF=ED+DF=a+1+a=OB=2,$
$\therefore a=\frac {1}{2},\therefore DF=OF=1+a=\frac {3}{2}.$
$\therefore D(-\frac {3}{2},\frac {3}{2}).$
设直线$l_{1}$的函数表达式为$y=kx+1$,则$\frac {3}{2}=-\frac {3}{2}k+1,$
解得$k=-\frac {1}{3}$,
∴直线$l_{1}$的函数表达式为$y=-\frac {1}{3}x+1.$

如答图②,直线$y=\frac {1}{2}x+1$绕点$A$逆时针旋转$45^{\circ }$后的图象为直线$l_{2}$,过点$B$作$BD⊥$直线$l_{2}$于点$D$,过点$D$作$DF⊥y$轴于点$F$,作$DE⊥x$轴于点$E$,则$△ABD$为等腰直角三角形.
同理可证$△ADF\cong △BDE.$
设$DF=b$,则$DE=b.$
∵点$A(0,1)$,点$B(-2,0),$
$\therefore AF=BE=1+b,BO=BE+OE=b+1+b=2,$
$\therefore b=\frac {1}{2},\therefore D(-\frac {1}{2},-\frac {1}{2}).$
设直线$l_{2}$的函数表达式为$y=kx+1,$
则$-\frac {1}{2}=-\frac {1}{2}k+1$,解得$k=3,$
∴直线$l_{2}$的函数表达式为$y=3x+1.$
综上可知,旋转后的函数图象对应的函数关系式是$y=-\frac {1}{3}x+1$或$y=3x+1.$
3. 如图,直线 $ y = -\frac{4}{3}x + 8 $ 与 $ x $ 轴、$ y $ 轴分别交于点 $ A $,$ B $,点 $ D $ 在 $ y $ 轴的负半轴上. 若将 $ \triangle DAB $ 沿直线 $ AD $ 折叠,点 $ B $ 恰好落在 $ x $ 轴正半轴上的点 $ C $ 处.
(1) 求 $ AB $ 的长和点 $ C $ 的坐标;
(2) 求直线 $ CD $ 的函数表达式.

(1) 求 $ AB $ 的长和点 $ C $ 的坐标;
(2) 求直线 $ CD $ 的函数表达式.

答案:解:
(1)
∵直线$y=-\frac {4}{3}x+8$与$x$轴、$y$轴分别交于点$A$,$B$,
∴$A(6,0)$,$B(0,8)$,
∴$OA=6$,$OB=8.$
$\therefore AB=\sqrt {6^{2}+8^{2}}=10.$
∵将$△DAB$沿直线$AD$折叠得到$△DAC,$
$\therefore AC=AB=10,\therefore OC=OA+AC=16.$
∵点$C$在$x$轴的正半轴上,
∴$C(16,0).$
(2)设$D(0,y)(y<0).$
由题意可知$CD=BD$,则$CD^{2}=BD^{2}.$
在$Rt△OCD$中,由勾股定理,得$16^{2}+y^{2}=(8-y)^{2},$
解得$y=-12$,
∴$D(0,-12).$
设直线$CD$的函数表达式为$y=kx-12,$
则$16k-12=0$,解得$k=\frac {3}{4},$
∴直线$CD$的函数表达式为$y=\frac {3}{4}x-12.$
(1)
∵直线$y=-\frac {4}{3}x+8$与$x$轴、$y$轴分别交于点$A$,$B$,
∴$A(6,0)$,$B(0,8)$,
∴$OA=6$,$OB=8.$
$\therefore AB=\sqrt {6^{2}+8^{2}}=10.$
∵将$△DAB$沿直线$AD$折叠得到$△DAC,$
$\therefore AC=AB=10,\therefore OC=OA+AC=16.$
∵点$C$在$x$轴的正半轴上,
∴$C(16,0).$
(2)设$D(0,y)(y<0).$
由题意可知$CD=BD$,则$CD^{2}=BD^{2}.$
在$Rt△OCD$中,由勾股定理,得$16^{2}+y^{2}=(8-y)^{2},$
解得$y=-12$,
∴$D(0,-12).$
设直线$CD$的函数表达式为$y=kx-12,$
则$16k-12=0$,解得$k=\frac {3}{4},$
∴直线$CD$的函数表达式为$y=\frac {3}{4}x-12.$