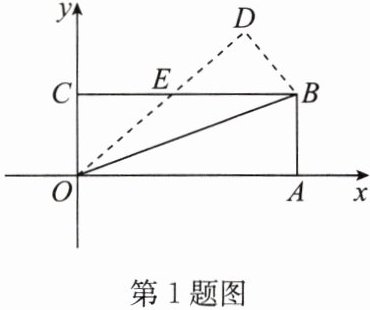
1. 如图,在平面直角坐标系 $xOy$ 中,$O$ 为坐标原点,$A(3,0)$,$B(3,1)$,$C(0,1)$,将 $\triangle OAB$ 沿直线 $OB$ 折叠,使得点 $A$ 落在点 $D$ 处,$OD$ 与 $BC$ 交于点 $E$,则 $OD$ 所在直线的函数表达式为(
A.$y= \frac{5}{4}x$
B.$y= \frac{4}{5}x$
C.$y= \frac{4}{3}x$
D.$y= \frac{3}{4}x$
D
)
A.$y= \frac{5}{4}x$
B.$y= \frac{4}{5}x$
C.$y= \frac{4}{3}x$
D.$y= \frac{3}{4}x$
答案:1.D 点拨:由O为坐标原点,A(3,0),B(3,1),C(0,1),知四边形ABCO是长方形,
∴OA//BC,
∴∠EBO=∠AOB.
又
∵∠EOB=∠AOB,
∴∠EOB=∠EBO,
∴OE=BE;设点E的坐标为(m,1),则OE=BE=3−m,CE=m.
在Rt△OCE中,OE²=OC²+CE²,
∴(3−m)²=1²+m²,
∴m=$\frac{4}{3}$.
∴点E的坐标为($\frac{4}{3}$,1).
设OD所在直线的函数表达式为y=kx,
将($\frac{4}{3}$,1)代入y=kx中,得1=$\frac{4}{3}$k,解得k=$\frac{3}{4}$,
∴OD所在直线的函数表达式为y=$\frac{3}{4}$x.故选D.
∴OA//BC,
∴∠EBO=∠AOB.
又
∵∠EOB=∠AOB,
∴∠EOB=∠EBO,
∴OE=BE;设点E的坐标为(m,1),则OE=BE=3−m,CE=m.
在Rt△OCE中,OE²=OC²+CE²,
∴(3−m)²=1²+m²,
∴m=$\frac{4}{3}$.
∴点E的坐标为($\frac{4}{3}$,1).
设OD所在直线的函数表达式为y=kx,
将($\frac{4}{3}$,1)代入y=kx中,得1=$\frac{4}{3}$k,解得k=$\frac{3}{4}$,
∴OD所在直线的函数表达式为y=$\frac{3}{4}$x.故选D.
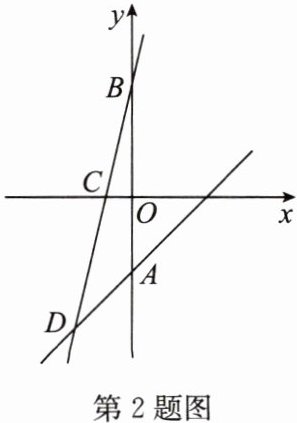
2. 如图,已知一次函数 $y = x - 2$ 的图象与 $y$ 轴交于点 $A$,一次函数 $y = 4x + b$ 的图象与 $y$ 轴交于点 $B$,且与 $x$ 轴以及一次函数 $y = x - 2$ 的图象分别交于点 $C$,$D$,点 $D$ 的坐标为 $(-2,m)$.
(1) 关于 $x$,$y$ 的方程组 $\begin{cases}y - x = -2,\\y - 4x = b\end{cases} $ 的解为
(2) 关于 $x$ 的不等式 $x - 2\geqslant 4x + b$ 的解集为
(3) 求四边形 $OADC$ 的面积.
(4) 在 $x$ 轴上是否存在点 $E$,使得以点 $C$,$D$,$E$ 为顶点的三角形是直角三角形?若存在,求出点 $E$ 的坐标;若不存在,请说明理由.
(1) 关于 $x$,$y$ 的方程组 $\begin{cases}y - x = -2,\\y - 4x = b\end{cases} $ 的解为
$\left\{\begin{array}{l} x=-2\\ y=-4\end{array}\right. $
.(2) 关于 $x$ 的不等式 $x - 2\geqslant 4x + b$ 的解集为
$x\leqslant - 2$
.(3) 求四边形 $OADC$ 的面积.
(4) 在 $x$ 轴上是否存在点 $E$,使得以点 $C$,$D$,$E$ 为顶点的三角形是直角三角形?若存在,求出点 $E$ 的坐标;若不存在,请说明理由.

答案:2.
(1)$\left\{\begin{array}{l} x=-2\\ y=-4\end{array}\right. $ 点拨:
∵点D(-2,m)在直线y=x - 2上,
∴m=-2 - 2=-4,
∴D(-2,-4).
∵一次函数y=x - 2的图象与一次函数y=4x + b的图象交于点D,
∴关于x,y的方程组$\left\{\begin{array}{l} y - x=-2\\ y - 4x=b\end{array}\right. $的解为$\left\{\begin{array}{l} x=-2\\ y=-4\end{array}\right. $.
(2)x≤ - 2
(3)解:在y=x - 2中,令x=0,得y=-2,从而A(0,-2).
由点D(-2,-4)在直线y=4x + b上,
得-4=4×(-2)+b,解得b=4,
∴直线BC的函数表达式为y=4x + 4.
易知C(-1,0),B(0,4),
∴AB=6,OC=1,OB=4.
∴S四边形OACD=S△BAD - S△BOC=$\frac{1}{2}$×6×2 - $\frac{1}{2}$×1×4=4.
(4)解:存在.如答图,当E为直角顶点时,过点D作DE1⊥x轴于点E1.
∵D(-2,-4),
∴E1(-2,0).
当C为直角顶点时,x轴上不存在满足条件的点E;
当D为直角顶点时,过点D作DE2⊥CD交x轴于点E2,设E2(t,0).
∵C(-1,0),E1(-2,0),
∴CE2=-1 - t,E1E2=-2 - t.
∵D(-2,-4),
∴DE1=4,CE1=-1 - (-2)=1.
在Rt△DE1E2中,
DE2²=DE1²+E1E2²=4²+(-2 - t)²=t²+4t + 20.
在Rt△CDE1中,CD²=1²+4²=17.
在Rt△CDE2中,CE2²=DE2²+CD²,
即(-1 - t)²=t²+4t + 20+17,解得t=-18.
∴E2(-18,0).
由上可得,点E的坐标为(-2,0)或(-18,0).
(1)$\left\{\begin{array}{l} x=-2\\ y=-4\end{array}\right. $ 点拨:
∵点D(-2,m)在直线y=x - 2上,
∴m=-2 - 2=-4,
∴D(-2,-4).
∵一次函数y=x - 2的图象与一次函数y=4x + b的图象交于点D,
∴关于x,y的方程组$\left\{\begin{array}{l} y - x=-2\\ y - 4x=b\end{array}\right. $的解为$\left\{\begin{array}{l} x=-2\\ y=-4\end{array}\right. $.
(2)x≤ - 2
(3)解:在y=x - 2中,令x=0,得y=-2,从而A(0,-2).
由点D(-2,-4)在直线y=4x + b上,
得-4=4×(-2)+b,解得b=4,
∴直线BC的函数表达式为y=4x + 4.
易知C(-1,0),B(0,4),
∴AB=6,OC=1,OB=4.
∴S四边形OACD=S△BAD - S△BOC=$\frac{1}{2}$×6×2 - $\frac{1}{2}$×1×4=4.
(4)解:存在.如答图,当E为直角顶点时,过点D作DE1⊥x轴于点E1.
∵D(-2,-4),
∴E1(-2,0).
当C为直角顶点时,x轴上不存在满足条件的点E;
当D为直角顶点时,过点D作DE2⊥CD交x轴于点E2,设E2(t,0).
∵C(-1,0),E1(-2,0),
∴CE2=-1 - t,E1E2=-2 - t.
∵D(-2,-4),
∴DE1=4,CE1=-1 - (-2)=1.
在Rt△DE1E2中,
DE2²=DE1²+E1E2²=4²+(-2 - t)²=t²+4t + 20.
在Rt△CDE1中,CD²=1²+4²=17.
在Rt△CDE2中,CE2²=DE2²+CD²,
即(-1 - t)²=t²+4t + 20+17,解得t=-18.
∴E2(-18,0).
由上可得,点E的坐标为(-2,0)或(-18,0).