1. 如图,直线 $ y = x + 4 $ 与两坐标轴分别交于 $ A $,$ B $ 两点,$ C $ 是线段 $ OB $ 的中点,$ D $,$ E $ 分别是直线 $ AB $、$ y $ 轴上的动点,则 $ \triangle CDE $ 周长的最小值是( )

A.$ 3\sqrt{7} $
B.$ 3\sqrt{10} $
C.$ 2\sqrt{7} $
D.$ 2\sqrt{10} $

A.$ 3\sqrt{7} $
B.$ 3\sqrt{10} $
C.$ 2\sqrt{7} $
D.$ 2\sqrt{10} $
答案:
1.D 点拨:作点C关于直线AB的对称点F,关于直线AO的对称点G,连接DF,EG.
∵直线$ y = x + 4 $与两坐标轴分别交于 $ A $,$ B $ 两点,$ C $ 是线段 $ OB $ 的中点,
∴$ B(-4,0),C(-2,0).\therefore BO=4,OG=2,BG=6.$
易得$∠ABC=45^{\circ },\therefore △BCF$是等腰直角三角形,
∴$ BF=BC=2$.
由轴对称的性质,可得$ DF=DC,EC=EG $.
如答图,当点F,D,E,G在同一直线上时,$△CDE $的周长$=CD+DE+CE=DF+DE+EG=FG$,此时$△DEC $的周长最小.
在$Rt△BFG$中,$FG=\sqrt {BF^{2}+BG^{2}}=\sqrt {2^{2}+6^{2}}=2\sqrt {10}$,$\therefore △CDE $周长的最小值是$2\sqrt{10}$.故选D.

1.D 点拨:作点C关于直线AB的对称点F,关于直线AO的对称点G,连接DF,EG.
∵直线$ y = x + 4 $与两坐标轴分别交于 $ A $,$ B $ 两点,$ C $ 是线段 $ OB $ 的中点,
∴$ B(-4,0),C(-2,0).\therefore BO=4,OG=2,BG=6.$
易得$∠ABC=45^{\circ },\therefore △BCF$是等腰直角三角形,
∴$ BF=BC=2$.
由轴对称的性质,可得$ DF=DC,EC=EG $.
如答图,当点F,D,E,G在同一直线上时,$△CDE $的周长$=CD+DE+CE=DF+DE+EG=FG$,此时$△DEC $的周长最小.
在$Rt△BFG$中,$FG=\sqrt {BF^{2}+BG^{2}}=\sqrt {2^{2}+6^{2}}=2\sqrt {10}$,$\therefore △CDE $周长的最小值是$2\sqrt{10}$.故选D.

2. 如图,在平面直角坐标系中,点 $ A(6,0) $,点 $ P(0,m) $,将线段 $ PA $ 绕着点 $ P $ 逆时针旋转 $ 90^{\circ} $,得到线段 $ PB $,连接 $ AB $,$ OB $,则 $ OB + AB $ 的最小值为______.


答案:
2.$6\sqrt {5}$ 点拨:如答图①,当点P在y轴正半轴上时,作$BH⊥y$轴于点H.
∵$∠BHP=∠BPA=∠AOP=90^{\circ }$,
∴$∠BPH+∠APO=90^{\circ },∠APO+∠PAO=90^{\circ }$.
∴$∠BPH=∠PAO$.
又
∵$ PB=PA,\therefore △PBH≌△APO $,
∴$ PH=OA=6,BH=PO.\therefore B(m,6+m) $.

∴$ OB+AB=\sqrt {m^{2}+(m+6)^{2}}+\sqrt {(m-6)^{2}+(m+6)^{2}}$.
如答图②,欲求$ OB+AB=\sqrt {m^{2}+(m+6)^{2}}+\sqrt {(m-6)^{2}+(m+6)^{2}} $的最小值,相当于在直线$ y=x $上寻找一点$ Q(m,m) $,使得点Q到点$ M(0,-6),N(6,-6) $的距离和最小,作点M关于直线$ y=x $的对称点$ M'(-6,0) $,易知$ QM+QN=QM'+QN≥NM'$.
∵$ NM'=\sqrt {(6+6)^{2}+6^{2}}=6\sqrt {5} $,
∴$ QM+QN $的最小值为$6\sqrt {5}$,
∴$ OB+AB=\sqrt {m^{2}+(m+6)^{2}}+\sqrt {(m-6)^{2}+(m+6)^{2}} $的最小值为$6\sqrt {5}$.
2.$6\sqrt {5}$ 点拨:如答图①,当点P在y轴正半轴上时,作$BH⊥y$轴于点H.
∵$∠BHP=∠BPA=∠AOP=90^{\circ }$,
∴$∠BPH+∠APO=90^{\circ },∠APO+∠PAO=90^{\circ }$.
∴$∠BPH=∠PAO$.
又
∵$ PB=PA,\therefore △PBH≌△APO $,
∴$ PH=OA=6,BH=PO.\therefore B(m,6+m) $.

∴$ OB+AB=\sqrt {m^{2}+(m+6)^{2}}+\sqrt {(m-6)^{2}+(m+6)^{2}}$.
如答图②,欲求$ OB+AB=\sqrt {m^{2}+(m+6)^{2}}+\sqrt {(m-6)^{2}+(m+6)^{2}} $的最小值,相当于在直线$ y=x $上寻找一点$ Q(m,m) $,使得点Q到点$ M(0,-6),N(6,-6) $的距离和最小,作点M关于直线$ y=x $的对称点$ M'(-6,0) $,易知$ QM+QN=QM'+QN≥NM'$.
∵$ NM'=\sqrt {(6+6)^{2}+6^{2}}=6\sqrt {5} $,
∴$ QM+QN $的最小值为$6\sqrt {5}$,
∴$ OB+AB=\sqrt {m^{2}+(m+6)^{2}}+\sqrt {(m-6)^{2}+(m+6)^{2}} $的最小值为$6\sqrt {5}$.
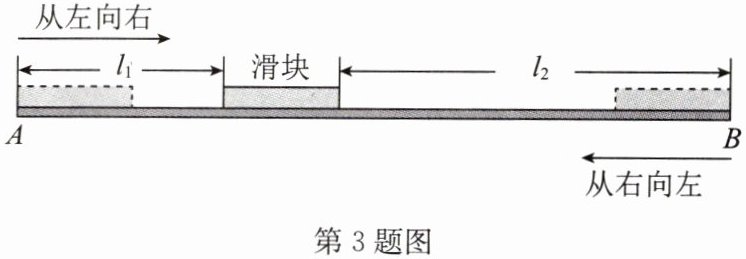
3. 某动力科学研究院实验基地内装有一段笔直的轨道 $ AB $,长度为 $ 1 \, m $ 的金属滑块在上面做往返滑动. 如图,滑块首先沿 $ AB $ 方向从左向右匀速滑动,滑动速度为 $ 9 \, m/s $,滑动开始前滑块左端与点 $ A $ 重合,当滑块右端到达点 $ B $ 时,滑块停顿 $ 2 \, s $,然后再以小于 $ 9 \, m/s $ 的速度匀速返回,直到滑块的左端与点 $ A $ 重合,滑动停止. 设时间为 $ t(s) $ 时,滑块左端离点 $ A $ 的距离为 $ l_1(m) $,右端离点 $ B $ 的距离为 $ l_2(m) $,记 $ d = l_1 - l_2 $,$ d $ 与 $ t $ 具有函数关系. 已知滑块在从左向右滑动的过程中,当 $ t = 4.5 $ 和 $ t = 5.5 $ 时,与之对应的 $ d $ 的两个值互为相反数;滑块从点 $ A $ 出发到最后返回点 $ A $,整个过程总用时 $ 27 \, s $(含停顿时间). 请你根据所给条件解决下列问题:
(1)
(2) 滑块从点 $ B $ 到点 $ A $ 的滑动过程中,求 $ d $ 与 $ t $ 之间的函数表达式;
(3) 在整个往返过程中,若 $ d = 18 $,求 $ t $ 的值.
(1)
由负到正
滑块从点 $ A $ 到点 $ B $ 的滑动过程中,$ d $ 的值______;(填“由负到正”或“由正到负”)(2) 滑块从点 $ B $ 到点 $ A $ 的滑动过程中,求 $ d $ 与 $ t $ 之间的函数表达式;
(3) 在整个往返过程中,若 $ d = 18 $,求 $ t $ 的值.

答案:3.
(1)由负到正 点拨:
∵$ d=l_{1}-l_{2} $,当滑块在A点时,$ l_{1}=0,d=-l_{2}<0 $,当滑块在B点时,$ l_{2}=0,d=l_{1}>0 $,
∴d的值由负到正.
(2)解:设轨道AB的长为$ n $ m,当滑块从左向右滑动时,
∵$ l_{1}+l_{2}+1=n $,
∴$ l_{2}=n-l_{1}-1 $,
∴$ d=l_{1}-l_{2}=l_{1}-(n-l_{1}-1)=2l_{1}-n+1=2×9t-n+1=18t-n+1 $,
∴d是t的一次函数.
∵当$ t=4.5 $和5.5时,与之对应的d的两个值互为相反数,
∴当$ t=5 $时,$ d=0 $,
∴$ 18×5-n+1=0 $,
∴$ n=91 $.
∴滑块从点A到点B所用的时间为$(91-1)÷9=10(s)$.
∵整个过程总用时27s(含停顿时间),当滑块右端到达点B时,滑块停顿2s,
∴滑块从点B返回到点A所用的时间为$27-10-2=15(s)$.
∴滑块返回的速度为$(91-1)÷15=6(m/s)$.
∴当$12≤t≤27$时,$ l_{2}=6(t-12) $,
∴$ l_{1}=91-1-l_{2}=90-6(t-12)=162-6t $,
∴$ l_{1}-l_{2}=162-6t-6(t-12)=-12t+234 $,
∴d与t之间的函数表达式为$ d=-12t+234(12≤t≤27) $.
(3)解:当$ d=18 $时,有两种情况:
由
(2)可得,①当$0≤t≤10$时,$18t-90=18$,
∴$ t=6 $;
②当$12≤t≤27$时,$-12t+234=18$,
∴$ t=18 $.
综上所述,当$ t=6 $或18时,$ d=18 $.
(1)由负到正 点拨:
∵$ d=l_{1}-l_{2} $,当滑块在A点时,$ l_{1}=0,d=-l_{2}<0 $,当滑块在B点时,$ l_{2}=0,d=l_{1}>0 $,
∴d的值由负到正.
(2)解:设轨道AB的长为$ n $ m,当滑块从左向右滑动时,
∵$ l_{1}+l_{2}+1=n $,
∴$ l_{2}=n-l_{1}-1 $,
∴$ d=l_{1}-l_{2}=l_{1}-(n-l_{1}-1)=2l_{1}-n+1=2×9t-n+1=18t-n+1 $,
∴d是t的一次函数.
∵当$ t=4.5 $和5.5时,与之对应的d的两个值互为相反数,
∴当$ t=5 $时,$ d=0 $,
∴$ 18×5-n+1=0 $,
∴$ n=91 $.
∴滑块从点A到点B所用的时间为$(91-1)÷9=10(s)$.
∵整个过程总用时27s(含停顿时间),当滑块右端到达点B时,滑块停顿2s,
∴滑块从点B返回到点A所用的时间为$27-10-2=15(s)$.
∴滑块返回的速度为$(91-1)÷15=6(m/s)$.
∴当$12≤t≤27$时,$ l_{2}=6(t-12) $,
∴$ l_{1}=91-1-l_{2}=90-6(t-12)=162-6t $,
∴$ l_{1}-l_{2}=162-6t-6(t-12)=-12t+234 $,
∴d与t之间的函数表达式为$ d=-12t+234(12≤t≤27) $.
(3)解:当$ d=18 $时,有两种情况:
由
(2)可得,①当$0≤t≤10$时,$18t-90=18$,
∴$ t=6 $;
②当$12≤t≤27$时,$-12t+234=18$,
∴$ t=18 $.
综上所述,当$ t=6 $或18时,$ d=18 $.