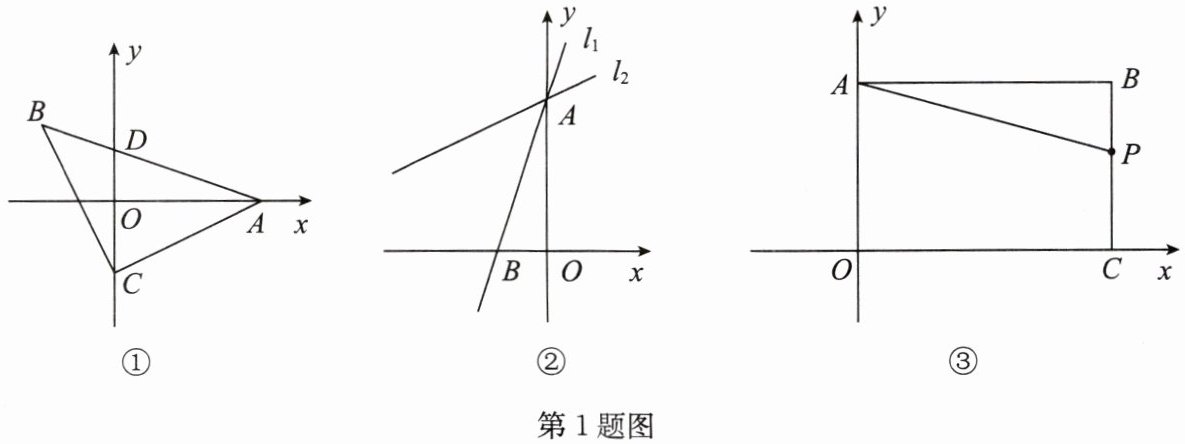
1.(1)如图①,在平面直角坐标系中,等腰$Rt \triangle ABC$,$\angle ACB = 90^{\circ}$,$AC = BC$,点$C的坐标为(0,-2)$,点$A的坐标为(4,0)$,求点$B$的坐标.
(2)如图②,在平面直角坐标系中,直线$l_{1}$:$y = 3x + 6分别与y$轴、$x轴交于点A$,$B$,将直线$l_{1}绕点A顺时针旋转45^{\circ}得到直线l_{2}$,求直线$l_{2}$的函数表达式.
(3)如图③,在平面直角坐标系中,点$B(6,4)$,过点$B作AB \perp y轴于点A$,作$BC \perp x轴于点C$,$P为线段BC$上的一个动点,点$M在直线y = x + 2$上.问点$A$,$P$,$M能否构成以AM$为腰的等腰直角三角形?若能,请求出点$M$的坐标;若不能,请说明理由.
(2)如图②,在平面直角坐标系中,直线$l_{1}$:$y = 3x + 6分别与y$轴、$x轴交于点A$,$B$,将直线$l_{1}绕点A顺时针旋转45^{\circ}得到直线l_{2}$,求直线$l_{2}$的函数表达式.
(3)如图③,在平面直角坐标系中,点$B(6,4)$,过点$B作AB \perp y轴于点A$,作$BC \perp x轴于点C$,$P为线段BC$上的一个动点,点$M在直线y = x + 2$上.问点$A$,$P$,$M能否构成以AM$为腰的等腰直角三角形?若能,请求出点$M$的坐标;若不能,请说明理由.

答案:
1.解:
(1)如答图①,过点B作BE⊥y轴于点E,
则∠BEC=∠AOC=90°.
∵∠ACB=90°=∠BCE+∠OCA=∠OCA+∠OAC,
∴∠BCE=∠CAO.
又
∵AC=CB,
∴△AOC≌△CEB(AAS).
∵C(0, -2),A(4,0),
∴CE=OA=4,BE=OC=2.
∴B(-2,2).
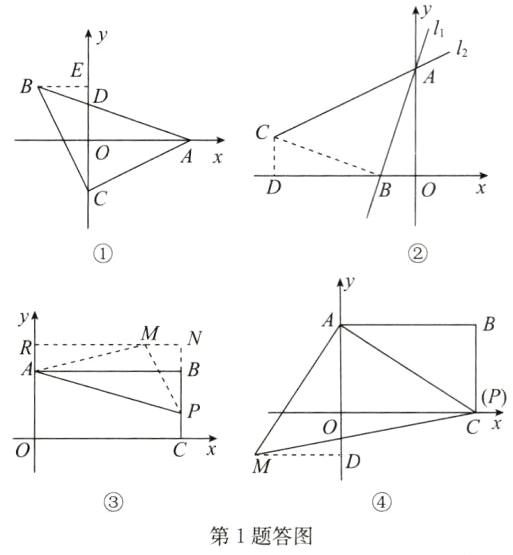
(2)由y=3x+6,得点A(0,6),B(-2,0).如答图②,过点B作BC⊥AB交直线l₂于点C,过点C作CD⊥x轴于点D,则△ABC为等腰直角三角形,∠ABC=90°,AB=BC.同
(1)可证明△AOB≌△BDC,于是BD=OA=6,CD=OB=2,
∴C(-8,2).
设直线l₂的函数表达式为y=kx+6,则-8k+6=2,解得k=$\frac{1}{2}$,
∴直线l₂的函数表达式为y=$\frac{1}{2}$x+6.
(3)能.当点M在AB上方时,
如答图③,过点M作RN//x轴,交y轴于点R,交CB的延长线于点N.
∵AB⊥y轴,BC⊥x轴,
∴∠OAB=90°,BC//y轴,
又
∵RN//x轴,
∴∠ARM=∠MNP=90°.
∵△APM是以AM为腰的等腰直角三角形,
∴∠AMP=90°,AM=PM,
∴∠AMR+∠PMN=90°.
∵∠AMR+∠MAR=90°,
∴∠MAR=∠PMN,
∴△AMR≌△MPN(AAS),
∴AR=MN.
设点M(a,a+2),
∴RM=a,NM=6 - a,OR=a+2,
∴AR=MN=6 - a,
∴OR=OA+AR,即4+6 - a=a+2,解得a=4,
∴M(4,6).
如答图④,当点P与点C重合时,有等腰Rt△AMP,∠MAP=90°,AM=AP,同
(1)可证明△AOC≌△MDA,于是AD=OC=6,MD=OA=4,此时M(-4,-2),在直线y=x+2上.
综上,点M的坐标为(4,6)或(-4,-2).
1.解:
(1)如答图①,过点B作BE⊥y轴于点E,
则∠BEC=∠AOC=90°.
∵∠ACB=90°=∠BCE+∠OCA=∠OCA+∠OAC,
∴∠BCE=∠CAO.
又
∵AC=CB,
∴△AOC≌△CEB(AAS).
∵C(0, -2),A(4,0),
∴CE=OA=4,BE=OC=2.
∴B(-2,2).

(2)由y=3x+6,得点A(0,6),B(-2,0).如答图②,过点B作BC⊥AB交直线l₂于点C,过点C作CD⊥x轴于点D,则△ABC为等腰直角三角形,∠ABC=90°,AB=BC.同
(1)可证明△AOB≌△BDC,于是BD=OA=6,CD=OB=2,
∴C(-8,2).
设直线l₂的函数表达式为y=kx+6,则-8k+6=2,解得k=$\frac{1}{2}$,
∴直线l₂的函数表达式为y=$\frac{1}{2}$x+6.
(3)能.当点M在AB上方时,
如答图③,过点M作RN//x轴,交y轴于点R,交CB的延长线于点N.
∵AB⊥y轴,BC⊥x轴,
∴∠OAB=90°,BC//y轴,
又
∵RN//x轴,
∴∠ARM=∠MNP=90°.
∵△APM是以AM为腰的等腰直角三角形,
∴∠AMP=90°,AM=PM,
∴∠AMR+∠PMN=90°.
∵∠AMR+∠MAR=90°,
∴∠MAR=∠PMN,
∴△AMR≌△MPN(AAS),
∴AR=MN.
设点M(a,a+2),
∴RM=a,NM=6 - a,OR=a+2,
∴AR=MN=6 - a,
∴OR=OA+AR,即4+6 - a=a+2,解得a=4,
∴M(4,6).
如答图④,当点P与点C重合时,有等腰Rt△AMP,∠MAP=90°,AM=AP,同
(1)可证明△AOC≌△MDA,于是AD=OC=6,MD=OA=4,此时M(-4,-2),在直线y=x+2上.
综上,点M的坐标为(4,6)或(-4,-2).