1. 如图,CD为△ABC的中线,M,N分别为直线CD上的点,且BM//AN,则CM+CN与CD之间的数量关系为

$CM+CN=2CD$
。
答案:$CM+CN=2CD$ 点拨:$\because BM// AN,$
$\therefore ∠NAD=∠MBD,∠N=∠BMD.$
又$\because CD$为$\triangle ABC$的中线,$\therefore AD=BD.$
$\therefore \triangle ADN\cong \triangle BDM(AAS).\therefore DN=DM.$
$\therefore CM+CN=CM+CD+DN=CM+CD+DM=CD+CD=2CD.$
$\therefore ∠NAD=∠MBD,∠N=∠BMD.$
又$\because CD$为$\triangle ABC$的中线,$\therefore AD=BD.$
$\therefore \triangle ADN\cong \triangle BDM(AAS).\therefore DN=DM.$
$\therefore CM+CN=CM+CD+DN=CM+CD+DM=CD+CD=2CD.$
2. 如图,在△ABC中,AD平分∠BAC,且AD⊥BC于点D,CE⊥AB于点E,交AD于点F。
(1)求证:BD= CD;
(2)若AF= BC,求证:AC-CE= EF。

(1)求证:BD= CD;
(2)若AF= BC,求证:AC-CE= EF。

答案:证明:
(1)$\because AD$平分$∠BAC,\therefore ∠BAD=∠CAD.$
$\because AD⊥BC,\therefore ∠ADB=∠ADC=90^{\circ }.$
又$\because AD=AD,\therefore \triangle ADB\cong \triangle ADC(ASA).$
$\therefore BD=CD.$
(2)$\because CE⊥AB,\therefore ∠AEF=∠CEB=90^{\circ }.$
$\because ∠AEF=∠FDC=90^{\circ },∠AFE=∠DFC,$
$\therefore ∠EAF=∠BCE.$
又$\because AF=BC,\therefore \triangle AEF\cong \triangle CEB(AAS).$
$\therefore AE=CE,EF=BE.$
$\because \triangle ADB\cong \triangle ADC,\therefore AB=AC.$
$\because AB - AE=BE,\therefore AC - CE=EF.$
(1)$\because AD$平分$∠BAC,\therefore ∠BAD=∠CAD.$
$\because AD⊥BC,\therefore ∠ADB=∠ADC=90^{\circ }.$
又$\because AD=AD,\therefore \triangle ADB\cong \triangle ADC(ASA).$
$\therefore BD=CD.$
(2)$\because CE⊥AB,\therefore ∠AEF=∠CEB=90^{\circ }.$
$\because ∠AEF=∠FDC=90^{\circ },∠AFE=∠DFC,$
$\therefore ∠EAF=∠BCE.$
又$\because AF=BC,\therefore \triangle AEF\cong \triangle CEB(AAS).$
$\therefore AE=CE,EF=BE.$
$\because \triangle ADB\cong \triangle ADC,\therefore AB=AC.$
$\because AB - AE=BE,\therefore AC - CE=EF.$
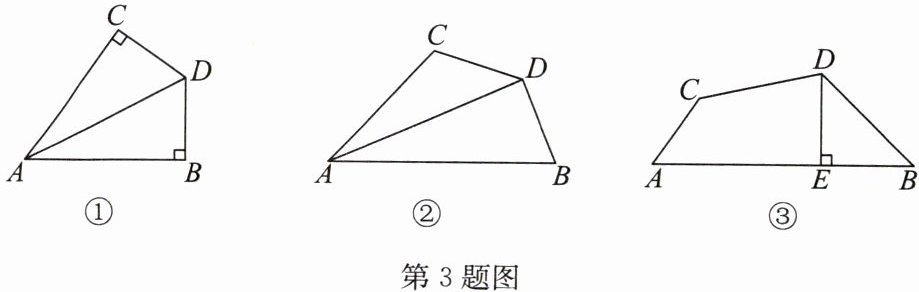
3. 感知:如图①,AD平分∠BAC,∠B+∠C= 180°,∠B= 90°。易知:DB= DC。(不需证明)
(1)探究:如图②,AD平分∠BAC,∠ABD+∠ACD= 180°,∠ABD<90°,求证:DB= DC;
(2)应用:如图③,在四边形ABDC中,∠B= 45°,∠C= 135°,DB= DC,DE⊥AB于点E,求证:AB-AC= 2BE。
(1)探究:如图②,AD平分∠BAC,∠ABD+∠ACD= 180°,∠ABD<90°,求证:DB= DC;
(2)应用:如图③,在四边形ABDC中,∠B= 45°,∠C= 135°,DB= DC,DE⊥AB于点E,求证:AB-AC= 2BE。

答案:
证明:
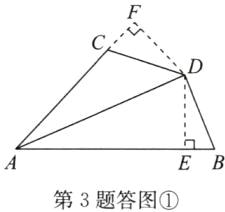
(1)如答图①,过点D作$DE⊥AB$于点E,$DF⊥AC$,交AC的延长线于点F,则$∠DEB=∠DEA=∠F=90^{\circ }.$
$\because AD$平分$∠BAC,\therefore ∠DAF=∠DAE.$
又$\because AD=AD,\therefore \triangle ADE\cong \triangle ADF(AAS).$
$\therefore DE=DF.$
$\because ∠B+∠ACD=180^{\circ },∠DCF+∠ACD=180^{\circ },$
$\therefore ∠B=∠DCF.$
又$\because ∠F=∠DEB,\therefore \triangle DEB\cong \triangle DFC(AAS).$
$\therefore DB=DC.$
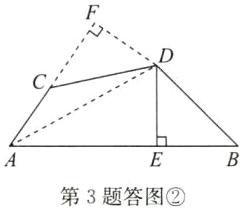
(2)如答图②,连接AD,作$DF⊥AC$,交AC的延长线于点F.
$\because ∠ACD=135^{\circ },\therefore ∠FCD=180^{\circ }-∠ACD=45^{\circ }.$
$\because ∠B=45^{\circ },\therefore ∠FCD=∠B.$
在$\triangle DFC$和$\triangle DEB$中,$\left\{\begin{array}{l} ∠DFC=∠DEB=90^{\circ },\\ ∠DCF=∠B,\\ DC=DB,\end{array}\right. $
$\therefore \triangle DFC\cong \triangle DEB(AAS).$
$\therefore DF=DE,CF=BE.$
在$Rt\triangle ADF$和$Rt\triangle ADE$中,$\left\{\begin{array}{l} AD=AD,\\ DF=DE,\end{array}\right. $
$\therefore Rt\triangle ADF\cong Rt\triangle ADE(HL).$
$\therefore AF=AE.$
$\therefore AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE,$
$\therefore AB - AC=2BE.$
证明:
(1)如答图①,过点D作$DE⊥AB$于点E,$DF⊥AC$,交AC的延长线于点F,则$∠DEB=∠DEA=∠F=90^{\circ }.$
$\because AD$平分$∠BAC,\therefore ∠DAF=∠DAE.$
又$\because AD=AD,\therefore \triangle ADE\cong \triangle ADF(AAS).$
$\therefore DE=DF.$
$\because ∠B+∠ACD=180^{\circ },∠DCF+∠ACD=180^{\circ },$
$\therefore ∠B=∠DCF.$
又$\because ∠F=∠DEB,\therefore \triangle DEB\cong \triangle DFC(AAS).$
$\therefore DB=DC.$

(2)如答图②,连接AD,作$DF⊥AC$,交AC的延长线于点F.
$\because ∠ACD=135^{\circ },\therefore ∠FCD=180^{\circ }-∠ACD=45^{\circ }.$
$\because ∠B=45^{\circ },\therefore ∠FCD=∠B.$
在$\triangle DFC$和$\triangle DEB$中,$\left\{\begin{array}{l} ∠DFC=∠DEB=90^{\circ },\\ ∠DCF=∠B,\\ DC=DB,\end{array}\right. $
$\therefore \triangle DFC\cong \triangle DEB(AAS).$
$\therefore DF=DE,CF=BE.$
在$Rt\triangle ADF$和$Rt\triangle ADE$中,$\left\{\begin{array}{l} AD=AD,\\ DF=DE,\end{array}\right. $
$\therefore Rt\triangle ADF\cong Rt\triangle ADE(HL).$
$\therefore AF=AE.$
$\therefore AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE,$
$\therefore AB - AC=2BE.$
