1. 如图,在$\triangle ABC$中,$\angle BAC = 60^{\circ}$,$AD为\triangle ABC$的角平分线,且$AC = AB + BD$,则$\angle B$的度数为( )

A.$70^{\circ}$
B.$60^{\circ}$
C.$80^{\circ}$
D.$85^{\circ}$

A.$70^{\circ}$
B.$60^{\circ}$
C.$80^{\circ}$
D.$85^{\circ}$
答案:
C 点拨:如答图,在AC上取点E,使AE=AB,连接DE.
∵AD为△ABC的角平分线,
∴∠BAD=∠EAD.
又
∵AD=AD,
∴△ABD≌△AED(SAS),
∴BD=ED,∠B=∠AED.
∵AC=AB+BD,
∴AC=AE+DE.
又
∵AC=AE+EC,
∴ED=EC,
∴∠ECD=∠EDC;
∵∠AED=∠EDC+∠C,
∴∠B=2∠C;
∵∠BAC=60°,
∴∠B+∠C=120°.
∴∠B+$\frac{1}{2}$∠B=120°,
∴∠B=80°.故选C;

C 点拨:如答图,在AC上取点E,使AE=AB,连接DE.
∵AD为△ABC的角平分线,
∴∠BAD=∠EAD.
又
∵AD=AD,
∴△ABD≌△AED(SAS),
∴BD=ED,∠B=∠AED.
∵AC=AB+BD,
∴AC=AE+DE.
又
∵AC=AE+EC,
∴ED=EC,
∴∠ECD=∠EDC;
∵∠AED=∠EDC+∠C,
∴∠B=2∠C;
∵∠BAC=60°,
∴∠B+∠C=120°.
∴∠B+$\frac{1}{2}$∠B=120°,
∴∠B=80°.故选C;

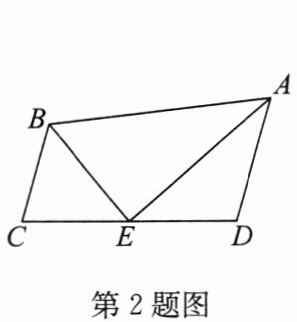
2. 如图,在四边形$ABCD$中,$AD// BC$.若$\angle DAB的平分线AE交CD于点E$,连接$BE$,且$BE平分\angle ABC$,则以下命题:①$BC + AD = AB$;②$E为CD$的中点;③$\angle AEB = 90^{\circ}$;④$S_{\triangle ABE} = \frac{1}{2}S_{四边形ABCD}$;⑤$BC = CE$.其中,正确的是______.(填序号)

答案:
①②③④ 点拨:如答图,在AB边上取点F,使BF=BC,连接EF.
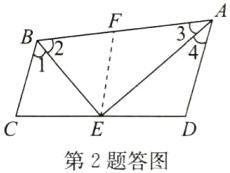
∵BE平分∠ABC,AE平分∠BAD,
∴∠1=∠2,∠3=∠4.
又
∵BF=BC,BE=BE,
∴△CBE≌△FBE(SAS).
∴CE=FE,∠CEB=∠FEB,∠C=∠BFE.
∵AD//BC,
∴∠C+∠D=180°.
∵∠BFE+∠AFE=180°,
∴∠AFE=∠D.
又
∵∠3=∠4,AE=AE,
∴△AEF≌△AED(AAS).
∴AD=AF,DE=FE,∠DEA=∠FEA.
∴CE=DE,即E为CD的中点,故②正确;
∵BF=BC,AD=AF,
∴BC+AD=BF+AF=AB,故①正确;
∵∠CEB=∠FEB,∠DEA=∠FEA,
∴∠AEB=90°,故③正确.由答图中两对全等三角形可知$S_{\triangle ABE}=\frac{1}{2}S_{四边形ABCD}$,故④正确;
BC与CE的大小无法证明,故⑤不正确.
综上,答案为①②③④.
①②③④ 点拨:如答图,在AB边上取点F,使BF=BC,连接EF.

∵BE平分∠ABC,AE平分∠BAD,
∴∠1=∠2,∠3=∠4.
又
∵BF=BC,BE=BE,
∴△CBE≌△FBE(SAS).
∴CE=FE,∠CEB=∠FEB,∠C=∠BFE.
∵AD//BC,
∴∠C+∠D=180°.
∵∠BFE+∠AFE=180°,
∴∠AFE=∠D.
又
∵∠3=∠4,AE=AE,
∴△AEF≌△AED(AAS).
∴AD=AF,DE=FE,∠DEA=∠FEA.
∴CE=DE,即E为CD的中点,故②正确;
∵BF=BC,AD=AF,
∴BC+AD=BF+AF=AB,故①正确;
∵∠CEB=∠FEB,∠DEA=∠FEA,
∴∠AEB=90°,故③正确.由答图中两对全等三角形可知$S_{\triangle ABE}=\frac{1}{2}S_{四边形ABCD}$,故④正确;
BC与CE的大小无法证明,故⑤不正确.
综上,答案为①②③④.
3. 如图,$AB = AC$,$\angle B + \angle C = 180^{\circ}$,$\angle EAF = \frac{1}{2}\angle BAC$,求证:$EF = BE + CF$.


答案:
证明:如答图,延长EB到点H,使BH=CF,连接AH.

∵∠ABD+∠C=180°,∠ABD+∠ABH=180°,
∴∠C=∠ABH.
又
∵AB=AC.
∴△ABH≌△ACF(SAS),
∴∠CAF=∠BAH,AH=AF.
∵∠EAF=$\frac{1}{2}$∠BAC,
∴∠EAF=∠CAF+∠BAE=∠HAB+∠BAE=∠HAE.
又
∵AH=AF,AE=AE,
∴△HAE≌△FAE(SAS),
∴EF=EH.
∵EH=BE+HB=BE+CF,
∴EF=BE+CF.
证明:如答图,延长EB到点H,使BH=CF,连接AH.

∵∠ABD+∠C=180°,∠ABD+∠ABH=180°,
∴∠C=∠ABH.
又
∵AB=AC.
∴△ABH≌△ACF(SAS),
∴∠CAF=∠BAH,AH=AF.
∵∠EAF=$\frac{1}{2}$∠BAC,
∴∠EAF=∠CAF+∠BAE=∠HAB+∠BAE=∠HAE.
又
∵AH=AF,AE=AE,
∴△HAE≌△FAE(SAS),
∴EF=EH.
∵EH=BE+HB=BE+CF,
∴EF=BE+CF.