1. 角是轴对称图形,
角平分线
是它的对称轴.答案:角平分线
解析:
角平分线所在的直线
2. 角平分线的性质定理:角平分线上的点到角两边的距离
相等
.答案:相等
3. 角平分线性质定理的逆定理:角的内部到角两边距离相等的点在
角的平分线上
.答案:角的平分线上
4. 三角形三个角的平分线相交于同一点,这个点到三角形
三边
的距离相等.答案:三边
1. 如图,∠ABC 的平分线与△ABC 的外角的平分线相交于点 D,连接 AD. 求证:AD 是△ABC 的外角的平分线.
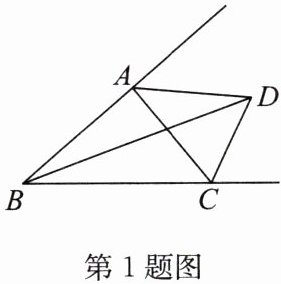

答案:
证明:如答图,过点D分别作AB,AC,BC的垂线,垂足分别为E,G,F.
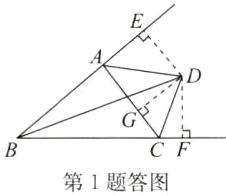
∵点D在∠ABC的平分线上,且DE⊥AB,DF⊥BC,
∴DE=DF.
同理DG=DF,
∴DG=DE.
又
∵DE⊥AB,DG⊥AC,
∴点D在∠EAC的平分线上,即AD是△ABC的外角的平分线.
证明:如答图,过点D分别作AB,AC,BC的垂线,垂足分别为E,G,F.

∵点D在∠ABC的平分线上,且DE⊥AB,DF⊥BC,
∴DE=DF.
同理DG=DF,
∴DG=DE.
又
∵DE⊥AB,DG⊥AC,
∴点D在∠EAC的平分线上,即AD是△ABC的外角的平分线.
2. 如图,在△ABC 中,∠C= 90°,AD 平分∠CAB,DE⊥AB 于点 E,点 F 在 AC 边上,BE= FC. 求证:BD= DF.
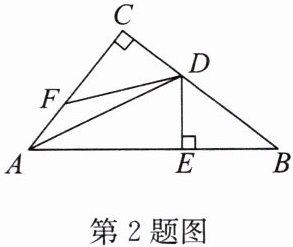

答案:证明:
∵∠C=90°,AD平分∠CAB,DE⊥AB于点E,
∴DC=DE.
在△DCF和△DEB中,{DC=DE,∠C=∠DEB=90°,CF=EB,
∴△DCF≌△DEB(SAS).
∴BD=DF.
∵∠C=90°,AD平分∠CAB,DE⊥AB于点E,
∴DC=DE.
在△DCF和△DEB中,{DC=DE,∠C=∠DEB=90°,CF=EB,
∴△DCF≌△DEB(SAS).
∴BD=DF.