1. 在三角形中,连接一个
顶点
与它的对边中点
的线段,叫作三角形的中线. 三角形的中线平分该三角形的面积.答案:顶点 中点
2. 在三角形中,一个内角的平分线与这个角的对边相交,这个角的
顶点
与交点
之间的线段叫作三角形的角平分线.答案:顶点 交点
3. 从三角形的一个顶点向它的对边所在直线作垂线,
顶点
与垂足
之间的线段叫作三角形的高线,简称三角形的高.答案:顶点 垂足
1. 三角形的高、中线、角平分线都是(
A.直线
B.线段
C.射线
D.以上情况都有
B
)A.直线
B.线段
C.射线
D.以上情况都有
答案:B
2. 不一定在三角形内部的线段是(
A.三角形的角平分线
B.三角形的中线
C.三角形的高
D.以上都不对
C
)A.三角形的角平分线
B.三角形的中线
C.三角形的高
D.以上都不对
答案:C
3. 若一个三角形的三条高所在的直线的交点在三角形的外部,则此三角形是
钝角
三角形.答案:钝角
4. 如图.
(1) $AD$ 是 $\triangle ABC$ 的角平分线,则 $\angle$
(2) $AE$ 是 $\triangle ABC$ 的中线,则
(3) $AF$ 是 $\triangle ABC$ 的高,则 $\angle$
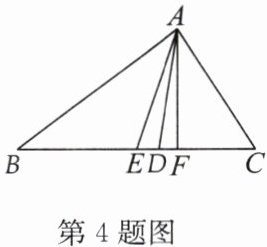
(1) $AD$ 是 $\triangle ABC$ 的角平分线,则 $\angle$
BAD
$=\angle$DAC
$=\frac{1}{2}\angle$BAC
;(2) $AE$ 是 $\triangle ABC$ 的中线,则
BE
$=$EC
$=\frac{1}{2}$BC
;(3) $AF$ 是 $\triangle ABC$ 的高,则 $\angle$
AFB
$=\angle$AFC
$=90^{\circ}$.
答案:
(1)BAD DAC BAC
(2)BE EC BC
(3)AFB AFC
(1)BAD DAC BAC
(2)BE EC BC
(3)AFB AFC
5. 若 $BD$ 是 $\triangle ABC$ 的中线,$AC = 10\ cm$,则 $CD = $
5
$cm$,$S_{\triangle ABC}:S_{\triangle BCD}= $2∶1
.答案:5 2∶1
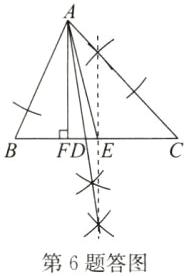
6. 如图,已知 $\triangle ABC$,过点 $A$ 画 $\triangle ABC$ 的角平分线 $AD$,中线 $AE$ 和高 $AF$.

答案:
解:如答图所示.
解:如答图所示.
